  
 o o

O 
A
- o o
Рис. 18.
Приведение системы сил к силе и паре сил
Определение.
Пусть задана система сил 1, …, 1, …,  n, приложенных твердому телу и задана произвольная точка О этого тела. Тогда вектор n, приложенных твердому телу и задана произвольная точка О этого тела. Тогда вектор  = ∑ = ∑ k называется главным вектором, вектор k называется главным вектором, вектор  o =∑ o =∑  o ( o ( k )называется главным моментом заданной системы сил относительно центра проведения О. k )называется главным моментом заданной системы сил относительно центра проведения О.
ОСНОВНАЯ ТЕОРЕМА СТАТИКИ.
Произвольная система сил, приложенных к твердому телу, эквивалентна одной силе, приложенной к некоторой точке О этого тела и равной главному вектору, и паре сил с моментом, свободным вектором , равным главному моменту системы сил относительно центра О.
Доказательство (рис. 19).
Согласно Лемме:
 k k { ko , ko , o (F k)} (к=1 о,n) , где o (F k)} (к=1 о,n) , где  ko= ko=  k k
Складывая  ko ,получим главный вектор ko ,получим главный вектор  =∑ =∑  k ; складывая k ; складывая o ( o ( k), получим главный момент k), получим главный момент  =∑ =∑ k k
        2 2
   20 20  1 1
      10 A2 10 A2
       A1 A1
O  1 1
- 10 - 10 - 20 20
Рис. 19 . (Рис. дан для n=2.)
Случаи приведения системы сил.
1      .Если .Если  =0, =0,  o ≠0,система находится в равновесии. o ≠0,система находится в равновесии.
2.  =0, =0,  o ≠0, система приводится к паре сил. o ≠0, система приводится к паре сил.
 
О  o o
О Случай 3.
Случай 2.
Рис.20.
3.Если  ≠0, и в точке 0: ≠0, и в точке 0: o=0, система приводится к равнодействующей, приложенной в точке 0. o=0, система приводится к равнодействующей, приложенной в точке 0.
4  . Если . Если  ≠0, и для точка 0 ≠0, и для точка 0  o≠0, в точке 0: o≠0, в точке 0:  o ││ F,т. е. система приводится к динамическому винту относительно этой точки. o ││ F,т. е. система приводится к динамическому винту относительно этой точки.
 
     О О   o o

Рис.21. Случай 4.
5.3.Условия равновесия произвольной пространственной системы сил.
Теорема Вариньона
Теорема.
 Для равновесия произвольной системы сил необходимо и достаточно ,чтобы векторная сумма сил и моментов сил относительно некоторого центра равнялась нулю. Для равновесия произвольной системы сил необходимо и достаточно ,чтобы векторная сумма сил и моментов сил относительно некоторого центра равнялась нулю.
( k)1 k)1
0 <=> ∑  k=0 - векторная форма условий равновесия k=0 - векторная форма условий равновесия
∑ o ( o ( k)=0 k)=0
 ∑ ∑  kх =0, ∑ kх =0, ∑ х ( х ( k)=0 - координатная форма условий равновесия. k)=0 - координатная форма условий равновесия.
<=> ∑  kу =0, ∑ kу =0, ∑ у ( у ( k)=0 k)=0
∑  kz =0, ∑ kz =0, ∑ z ( z ( k)=0 k)=0
Доказательство следует из основной теоремы статики.
Теорема Вариньона
Момент равнодействующей системы сил ,приложенных к твердому телу (если равнодействующая существует), относительно точки или оси равен сумме моментов сил системы относительно этой точки или оси.
Доказательство.
( 1 ,…, 1 ,…,  n) n)
 => ( => ( 1,…, 1,…,  n ,- n ,-  ) )
0=> ∑ o ( o ( k) - k) - o ( o ( )=0=> )=0=>  o ( o ( )= ∑ )= ∑ o ( o ( k) =0(к=1,n). k) =0(к=1,n).
5.4.Условия равновесия плоской системы сил.
Теорема 1.
Для равновесия системы сил , расположенной в плоскости 0ху, необходимо и достаточно, чтобы сумма проекции сил на координатные оси 0х и 0у и сумма моментов сил относительно оси 0z равнялась нулю.
∑F k х =0 , ∑F kу =0 , ∑ Мz ( k) =0. k) =0.
Доказательство следует из условий равновесия произвольной системы сил.
Теорема 2.
Для равновесия плоской системы сил необходимо и достаточно , чтобы суммы моментов относительно трех осей , перпендикулярных плоскости действия сил и не лежащих в одной плоскости , равнялись нулю (рис. 22)
∑Мz1 ( k)=0; ∑Мz2 ( k)=0; ∑Мz2 ( k)=0; ∑Мz3 ( k)=0; ∑Мz3 ( k)=0. k)=0.
  Y A1 Y A1
   Z1 A2 Z1 A2
  A3 A3
   Z2 Z2
Z3 X
Рис. 22.
 Y Y
  A A
J
   B B
  O X O X
Рис. 23.
Теорема 3.
Для равновесия плоской системы сил необходимо и достаточно, чтобы сумма моментов сил относительно двух осей , перпендикулярных плоскости действия сил, и сумма проекции сил на ось, не перпендикулярную плоскости, проходящей через указанные оси, равнялась нулю (рис. 23)
∑Мz1 ( k)=0 , ∑Мz2 ( k)=0 , ∑Мz2 ( k)=0 , ∑ ( k)=0 , ∑ ( k)=0. k)=0.
5.5.Применение условий равновесия к решению задач.
Условия равновесия системы сил, приложенных к твердому телу , позволяет находить неизвестные силы. При этом число неизвестных сил не должно превосходить числа условий равновесия. Если число неизвестных сил больше числа условий равновесия , задачи называются статистически неопределенными. Статистически неопределенные задачи рассматриваются в курсах механики деформируемых тел. При решении статистически определенных задач применяют аксиому «отвердевания».
Аксиома 5.
Равновесие деформируемого тела сохраняется при его отвердевании.
Глава 6. ВИДЫ СИЛ
6.1.Внешние и внутренние силы.
Внешними называются силы, действующие на рассматриваемую систему тел со стороны тел ,не принадлежащих этой системе.
Обозначение:  е ( exterieur –внешний) . е ( exterieur –внешний) .
Внутренними называются силы, с которыми тела системы и частицы тел действуют друг на друга.
Обозначение: i ( interieur – внутренний). i ( interieur – внутренний).
Свойство внутренних сил:
1.Векторная сумма внутренних сил системы равна нулю: ∑ i=0. i=0.
2.Векторная сумма моментов внутренних сил системы относительно произвольного центра равна нулю:∑  o( o( k i )=0. k i )=0.
Доказательство свойств следует из закона равенства действия и противодействия ,в соответствии с которым внутренние силы входят попарно противоположными.
6.2.Сосредоточенные и распределенные силы. Силы, действующие на самолет в полете.
Сила, приложенная к телу в какой-нибудь одной его точке , называется сосредоточенной. Силы, действующие на все точки данного обьема или данной части поверхности тела, называются распределенными.
Силы, которые в механике рассматриваются как сосредоточенные, являются абстракциями и, как правило, представляют собой равнодействующие некоторых распределенных сил.
Пример.
Силами, действующими на самолет в полете , являются: сила тяжести , аэродинамическая сила , тяга силовой установки.
Сила тяжести 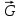 =m =m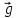 – обьемная сила, направленная к центру Земли , -равнодействующая сил тяжести частиц самолета. Линия действия этой силы проходит через центр тяжести. – обьемная сила, направленная к центру Земли , -равнодействующая сил тяжести частиц самолета. Линия действия этой силы проходит через центр тяжести.
Аэродинамическая сила  a= a=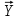 + + + + -поверхностная сила – главный вектор сил давления и трения , создаваемых воздушным потоком на элементах поверхности самолета. Составляющими аэродинамической силы по направлениям координатных осей скоростной системы являются: -поверхностная сила – главный вектор сил давления и трения , создаваемых воздушным потоком на элементах поверхности самолета. Составляющими аэродинамической силы по направлениям координатных осей скоростной системы являются:
- подьемная сила 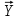 - направлена вверх по нормали к вектору скорости в плоской симметрии самолета; - направлена вверх по нормали к вектору скорости в плоской симметрии самолета;
- сила лобового сопротивления  – направлена противоположно воздушной скорости самолета; – направлена противоположно воздушной скорости самолета;
- боковая сила  - направлена перпендикулярно к - направлена перпендикулярно к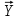 и и  (если скольжения нет , (если скольжения нет , =0) =0)
(Точка приложения аэродинамической силы называются центром давления . Главный момент сил давления и трения относительно центра давления называются моментом аэродинамических сил).
Тяга лобовой установки  – поверхностная сила , линия действия которой обычно составляет некоторый положительный угол с вектором воздушной скорости самолета (в задачах иногда угол пологают равным нулю – поверхностная сила , линия действия которой обычно составляет некоторый положительный угол с вектором воздушной скорости самолета (в задачах иногда угол пологают равным нулю
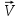
 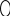      
  a a
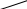 
 
 90 Q 90 Q
m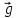 = =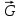
Р ис.24. ис.24.      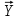 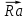
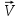      
 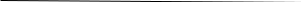  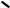
ц.g Х
Рис.25.
6.3. Реакция связей.
Связями называются тела, препятствующие движению данного тела. Реакциями связей называются силы, с которыми связи действуют на рассматриваемое тело. Реакция связи направлена в сторону, противоположную той, куда связь препятствует телу двигаться.
Примеры связей и их реакции.
Связь Направление возможной
реакции связи.
1  .Глаткая поверхность. По нормали к поверхности. .Глаткая поверхность. По нормали к поверхности.
  A A 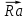
    
 

Рис. 26.
2.Гибкая нить. Вдоль нити – от тела.
              
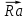
A
Рис.27.
3 .Цилиндрический шарнир (подшипник). .Цилиндрический шарнир (подшипник).
Y    a Перпендикулярно оси шарнира a Перпендикулярно оси шарнира
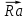 = = 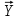 a + a + a; a;
   a, a,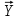 a , a ,
 Направлена условно в положительную Направлена условно в положительную
A   Xa Сторону осей координат Xa Сторону осей координат
Рис.28.
4  .Сферисический (шаровой) шарнир. .Сферисический (шаровой) шарнир.
   a Любое a Любое
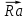 = =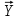 a + a + a+ a+ a, a,
 a, a, 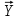 a, a,  a a
A 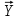 a направлены условно в положительную a направлены условно в положительную
сторону осей координат.
 a a
Шарнирами называются устройства, связывающие тела и позволяющие им совершать относительные вращения. Цилиндрический шарнир допускает вращение относительно одной оси и скольжение вдоль этой оси; сферический шарнир препятствует перемещению закрепленного тела по любому направлению, но допускает вращение относительно любой оси.
|
 Скачать 42.47 Kb.
Скачать 42.47 Kb.


 o
o

 o
o 1, …,
1, …,  n, приложенных твердому телу и задана произвольная точка О этого тела. Тогда вектор
n, приложенных твердому телу и задана произвольная точка О этого тела. Тогда вектор  = ∑
= ∑ k называется главным вектором, вектор
k называется главным вектором, вектор  o =∑
o =∑  o (
o ( k )называется главным моментом заданной системы сил относительно центра проведения О.
k )называется главным моментом заданной системы сил относительно центра проведения О. k
k 
 =∑
=∑


















 A1
A1




 .Если
.Если 
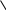
 . Если
. Если 








 О
О 
 Для равновесия произвольной системы сил необходимо и достаточно ,чтобы векторная сумма сил и моментов сил относительно некоторого центра равнялась нулю.
Для равновесия произвольной системы сил необходимо и достаточно ,чтобы векторная сумма сил и моментов сил относительно некоторого центра равнялась нулю. ∑
∑ 
 Y A1
Y A1

 Z1 A2
Z1 A2
 A3
A3

 Z2
Z2  Y
Y 
 A
A

 B
B O X
O X o(
o(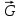
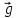 – обьемная сила, направленная к центру Земли , -равнодействующая сил тяжести частиц самолета. Линия действия этой силы проходит через центр тяжести.
– обьемная сила, направленная к центру Земли , -равнодействующая сил тяжести частиц самолета. Линия действия этой силы проходит через центр тяжести.
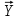 +
+ +
+ -поверхностная сила – главный вектор сил давления и трения , создаваемых воздушным потоком на элементах поверхности самолета. Составляющими аэродинамической силы по направлениям координатных осей скоростной системы являются:
-поверхностная сила – главный вектор сил давления и трения , создаваемых воздушным потоком на элементах поверхности самолета. Составляющими аэродинамической силы по направлениям координатных осей скоростной системы являются: – поверхностная сила , линия действия которой обычно составляет некоторый положительный угол с вектором воздушной скорости самолета (в задачах иногда угол пологают равным нулю
– поверхностная сила , линия действия которой обычно составляет некоторый положительный угол с вектором воздушной скорости самолета (в задачах иногда угол пологают равным нулю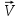

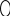

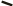


 a
a



 ис.24.
ис.24. 











 .Глаткая поверхность. По нормали к поверхности.
.Глаткая поверхность. По нормали к поверхности.
 A
A 
















 .Цилиндрический шарнир (подшипник).
.Цилиндрический шарнир (подшипник).

 a Перпендикулярно оси шарнира
a Перпендикулярно оси шарнира 




 .Сферисический (шаровой) шарнир.
.Сферисический (шаровой) шарнир.
