Билеты по геометрии 7 кл. билеты по геометрии 7класс новые. О пределение биссектрисы треугольника. Замечательное свойство биссектрис треугольника
 Скачать 1.3 Mb.
|
|
Билет №1. О 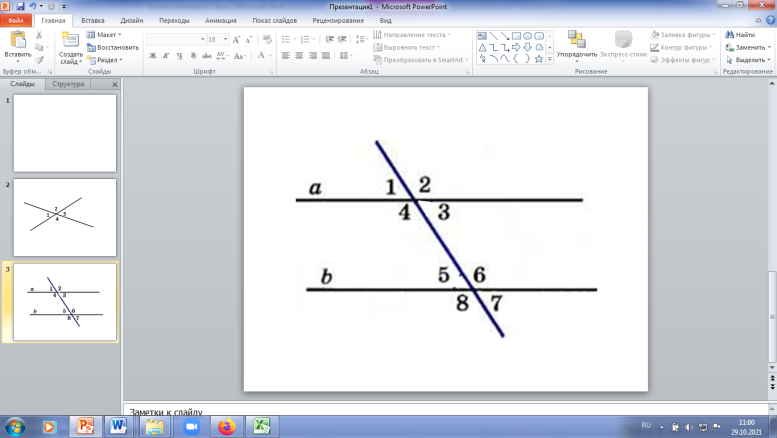 пределение биссектрисы треугольника. Замечательное свойство биссектрис треугольника.Первый признак равенства треугольников (доказательство). Дано: a||b, 5 = 600. Найдите 2.  Точка D на стороне AB треугольника ABC выбрана так, что AD = AC. Известно, что ∠CAB= 80° и ∠ACB = 59∘. Найдите угол DCB. Ответ дайте в градусах. _________________________________________________________________________________ Билет №2. Определение медианы треугольника. Замечательное свойство медиан треугольника. Т 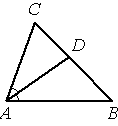 еорема о внешнем угле треугольника (доказательство).В  треугольнике ABC AD — биссектриса, угол C равен 62°, угол CAD равен 32°. Найдите угол B. Ответ дайте в градусах.Докажите равенство треугольников ABD и ACD, если АВ = АС и  1 = 2. Найдите ABD и ADB, если ACD = 380, ADC = 1020 .
___________________________________________________________________________ Билет №3. Определение высоты треугольника. Замечательное свойство высот треугольника. Признак равенства прямоугольных треугольников по гипотенузе и острому углу (доказательство). 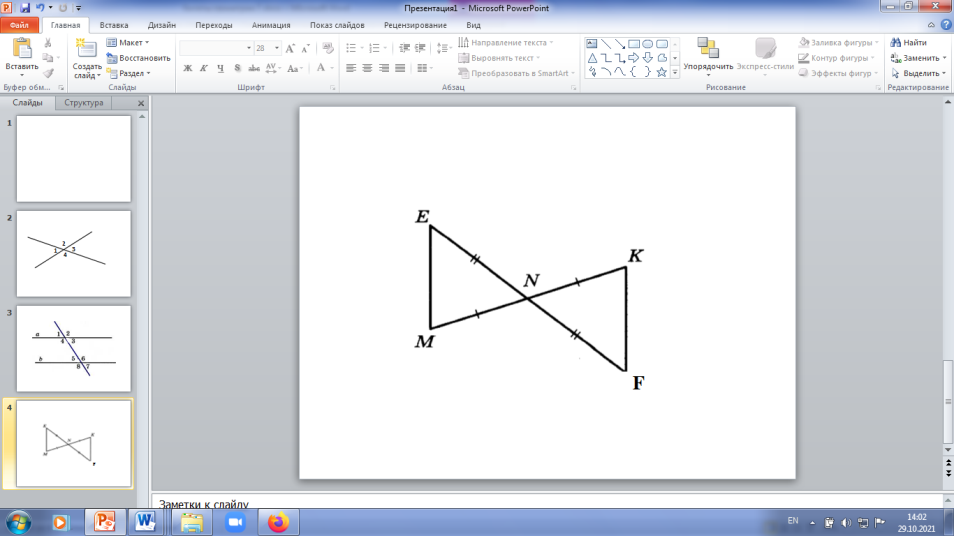 Дан равносторонний треугольник АВС. Найдите величину внешнего угла при вершине С. Докажите равенство треугольников MNE и KNF, если MN = NK и EN = NF. Найдите стороны ME и MN, если МК = 10см, КF = 8см. ______________________________________________________________________________________________ Билет №4. О 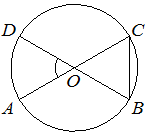 пределение равнобедренного треугольника. Теорема о сумме двух острых углов прямоугольного треугольника (доказательство). Отрезки AC и BD — диаметры окружности с центром O. Угол ACB равен 56°. Найдите угол AOD. Ответ дайте в градусах. 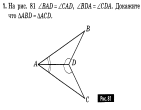 На рисунке BAD = СAD, ADB = ADС. Докажите, что B = С.Билет №5. Определение равностороннего треугольника. Сформулируйте и докажите признак параллельности двух прямых по внутренним односторонним углам. 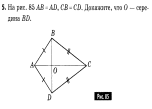 Один из острых углов прямоугольного треугольника равен 470. Найдите второй острый угол. На рисунке АВ = АD, СВ = СD. Докажите, что О - середина ВD. ____________________________________________________________________________ Билет №6. Определение окружности, радиуса, диаметра, хорды. Т 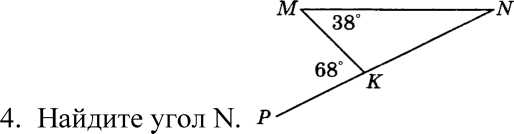 еорема о свойстве биссектрисы равнобедренного треугольника (доказательство).В треугольнике МКN угол М равен 380, внешний угол МКР равен 680. Найдите угол N. В треугольнике АВС А = 1000.Биссектрисы углов СС1 и ВВ1 пересекаются в точке D. Найдите угол BCD. ____________________________________________________________________________ Билет №7. О 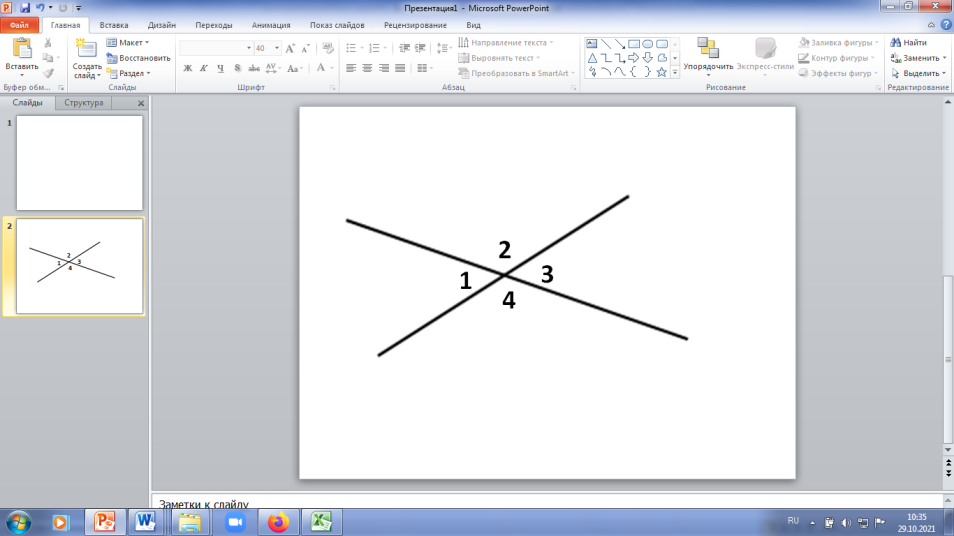 пределение параллельных прямых, параллельных отрезков. Теорема о сумме внутренних углов треугольника (доказательство). Найдите углы 1,3,4, изображенные на рисунке, если 2=1030.Точки А и В лежат по разные стороны от прямой МК, АМ и ВК – перпендикуляры к этой прямой. Докажите, что треугольники АМК и ВМК равны, если АК = ВМ. ____________________________________________________________________________ Билет №8. Определение внешнего угла треугольника. Свойство углов равнобедренного треугольника (доказательство). В треугольнике АВС А = 800, В = 600. Чему равен С? 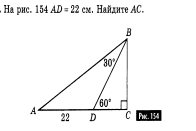 На рисунке AD = 22см. Найдите АС. Билет №9. Сформулируйте признаки равенства треугольников. Теорема о сумме двух острых углов прямоугольного треугольника (доказательство). О 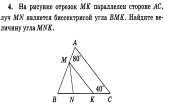 снование равнобедренного треугольника равно 9см, а боковая сторона на 2см больше. Найдите периметр треугольника.На рисунке отрезок МК параллелен стороне АС, луч MN является биссектрисой угла ВМК. Найдите величину угла MNK. ____________________________________________________________________________ Билет №10. О  пределение прямоугольного треугольника. Стороны и углы прямоугольного треугольника.Теорема о вертикальных углах (доказательство). Найдите острые углы треугольника MNK. В окружности с центром О проведены радиусы ОМ, ОК и ОN. Докажите, что треугольники МОК и NОК равны, если известно, что хорды МК и КNравны. ______________________________________________________________________________ Билет №11. Определение расстояния от точки до прямой. Неравенство треугольника.(теорема с доказательством). У 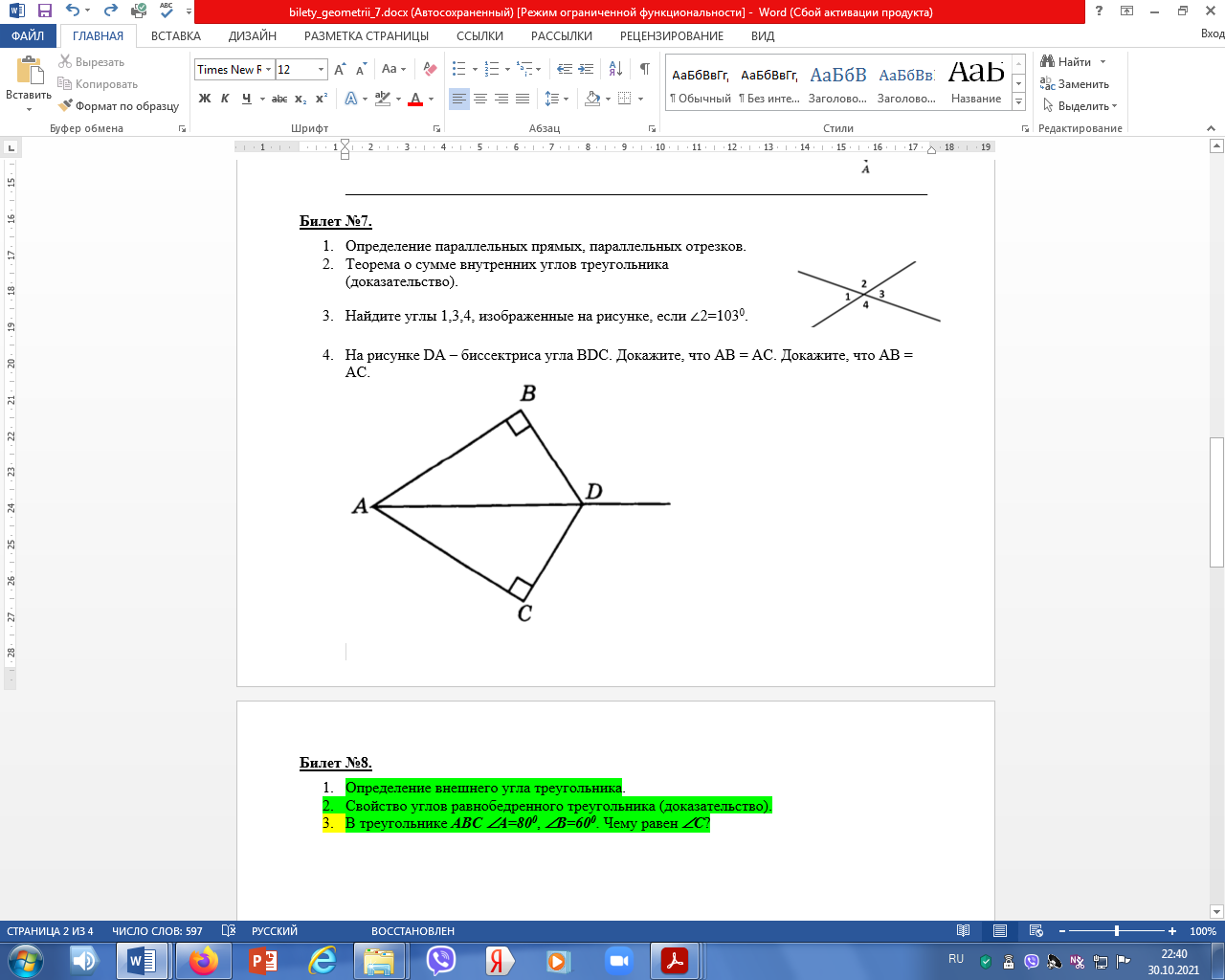 гол при вершине равнобедренного треугольника равен 480. Найдите углы при основании этого треугольника.На рисунке DA – биссектриса угла BDC. Докажите, что АВ = АС. _______________________________________________________________________________ Билет №12. Виды треугольников. Определение каждого вида треугольника. Неравенство треугольника. Признак равенства прямоугольных треугольников по катету и острому углу (доказательство). О  дин из смежных углов на 260 меньше другого. Найдите эти углы.На рисунке точка К является серединой отрезков AD и BC. Докажите, что прямые АВ и СD параллельны. Б 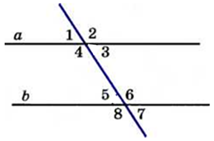 илет №13.Секущая. Виды углов при пересечении двух параллельных прямых третьей. Теорема о свойстве смежных углов (доказательство). Дано: a||b, 8 = 1200. Найдите 3. В треугольнике АВС стороны АВ и ВС равны. Точки М, Н и К – середины сторон АВ, ВС, АС соответственно. Докажите, что треугольники АМК и КНС равны. ____________________________________________________________________________ Билет №14. Определение вертикальных углов. Сформулируйте и докажите признак параллельности двух прямых по соответственным углам. 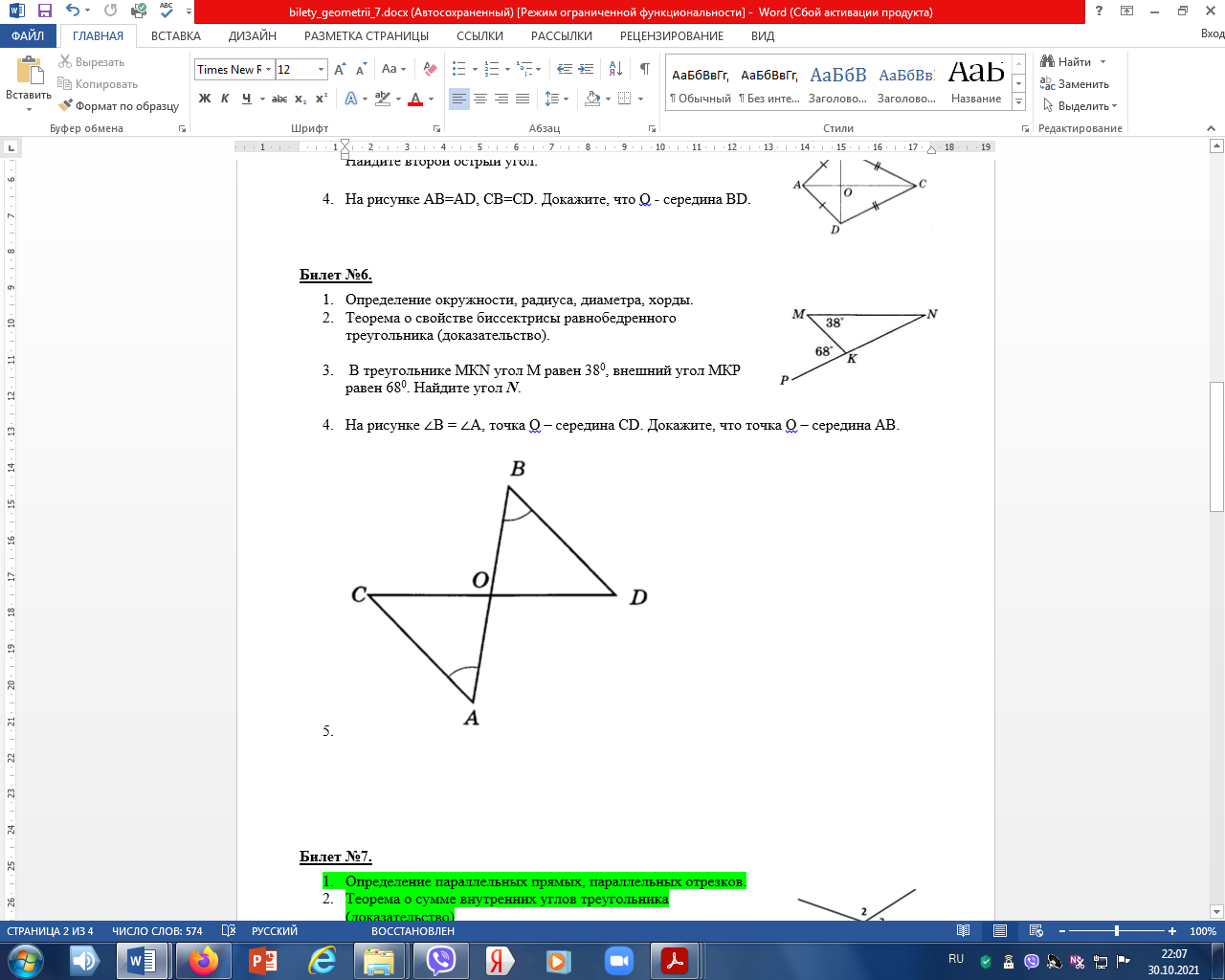 Найдите смежные углы, если их градусные меры относятся как 4:5. На рисунке B = A, точка О – середина CD. Докажите, что точка О – середина АВ.__________________________________________________________________________________ Билет №15. Определение перпендикулярных прямых. Сформулируйте и докажите свойство катета прямоугольного треугольника, лежащего против угла в 300. В 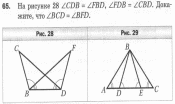 треугольнике ABC известно, что AB=BC, ∠ABC=106°. Найдите угол BCA. Ответ дайте в градусах. На рисунке СDВ = FBD, FDB = CBD. Докажите, что BСD = BFD.__________________________________________________________________________________
|