Екоеометрія. Економетрія2dfh. Обчислення вибіркових похибок параметрів регресії. Побудова довірчих інтервалів для істинних значень параметрів регресії, їх геометрична інтерпретація
 Скачать 86.71 Kb. Скачать 86.71 Kb.
|
|
Обчислення вибіркових похибок параметрів регресії. Побудова довірчих інтервалів для істинних значень параметрів регресії, їх геометрична інтерпретація Обчислимо стандартну вибіркову похибку вільного члена регресії (b0): знайдемо суму квадратів відхилень значень Х від їх середнього значення: 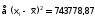 Знайдемо стандартну похибку вільного члена b0, за формулою 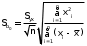 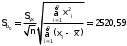 . . За таблицями Стьюдента, при довірчій ймовірності (р)=95% (рівнем значущості α=0,05) та кількістю ступенів свободи 21 знайдемо значення ймовірнісного коефіцієнта tp = 2,079. У цьому разі гранична похибка вільного члена  = 5240,30 = 5240,30Визначивши її, будуємо довірчий інтервал для істинного значення параметра β0: 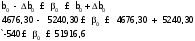 Між -540 і 51916,6 з ймовірністю 95% лежить істинне значення параметра β0 генеральної сукупності. 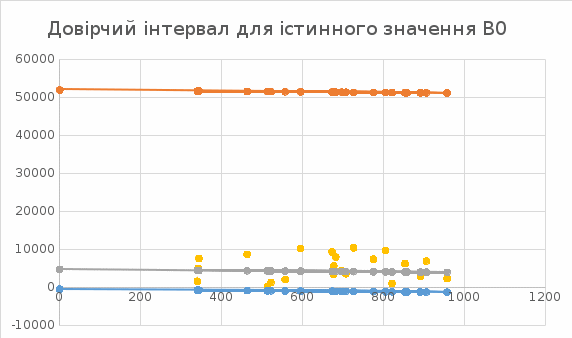 Обчислим стандартну вибіркову похибку параметра b1 за формулою 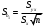 Sb1= 3,64. tp за таблицями розподілу Стьюдента дорівнює 2,079. У цьому разі гранична похибка 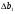 дорівнює 7,57. дорівнює 7,57.Звідси істинне значення параметра регресії β1 з ймовірністю 95% знаходиться в межах: 6,73 ≤ β1 ≤ 8,41 Геометрично довірчий інтервал для істинного значення β1 - це пара прямих, які перетинаються у точці 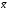 і і 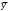 (668,7; 5270,74). (668,7; 5270,74).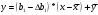 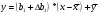 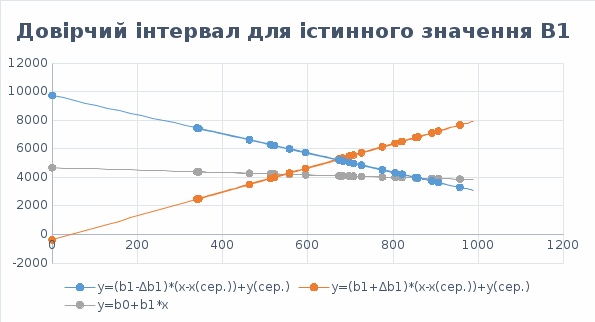 Кут нахилу прямої регресії знаходиться в межах: 81 ≤ɡ≤ 83. Розрахунок вибіркової похибки моделі. Побудова довірчого інтервалу для середнього прогнозного значення результуючої змінної, його геометрична інтерпретація Знаючи вибіркові похибки параметрів парної лінійної кореляційно-регресійної моделі можна знайти вибіркову похибку всієї моделі. Для цього обчислимо стандартну вибіркову похибку парної лінійної кореляційно-регресійної моделі за цією формулою: 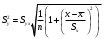 Вибіркова похибка 865,85. Визначимо у теоретичне для х = 534,0, утеор.= 5127,04. Граничну вибіркову похибку та довірчий інтервал для фактичного значення результуючої змінної при х =534,0, при довірчій ймовірності 95% знаходимо: Δу(теор.) = 1800,092
Це означає, що з ймовірністю 95% фактичне значення У при Х=534,0, повинно лежати в межах від 3326,948 до 6927,132. Геометрично це смуга між двома гіперболами, рівняння цих гіпербол знаходимо за формулами: 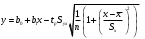 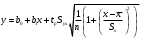 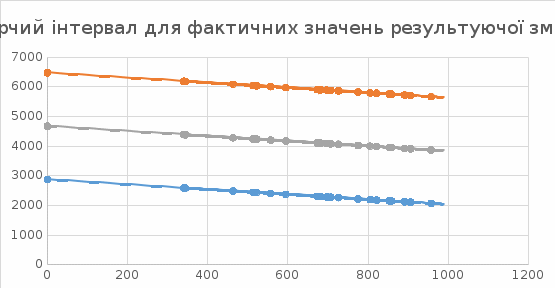 Стандартна похибка моделі характеризує непояснену варіацію результуючої змінної, яка завжди наявна при кореляційному зв’язку між змінними, це ще одне підтвердження кореляційного зв’язку між змінними. Обчислення похибки індивідуального прогнозу. Побудова довірчого інтервалу для індивідуального прогнозного значення результуючої змінної, його геометрична інтерпретація. Для того, щоб оцінити конкретне значення у при даному х, а не умовно середнє значення у, потрібно обчислити похибку індивідуального прогнозу. Спочатку знайдемо стандартну похибку оцінювання індивідуального прогнозу за формулою:  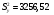 . .Гранична вибіркова похибка та довірчий інтервал для фактичного значення результуючої змінної при х =534,0, при довірчій ймовірності 95%: Δуі (теор.) = 5127,04
Це означає, що з ймовірністю 95% фактичне значення Y (в конкретному регіоні) при Х=534,0 повинно знаходитись в межах від -1643,26 до 11897,34. Довірчий інтервал для індивідуального прогнозу геометрично інтерпретується як смуга між двома гіперболами: 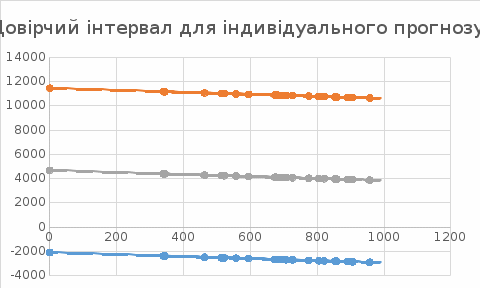 Оцінка коефіцієнта кореляції. Оскільки значення коефіцієнта кореляції (|r|=0,05) наближене до 0, тобто зв’язок між змінними слабкий, то розподіл наближається до нормального. Отже, обчислимо стандартну похибку коефіцієнта кореляції за цією формулою: 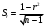 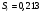 тоді довірчий інтервал для істинного значення коефіцієнта кореляції ƿ:
Отже, з довірчою ймовірністю 95% можна стверджувати, що істинне значення кореляції ƿ генеральної сукупності має лежати в межах від -0,392 до 0,492. Перевірка статистичної значущості параметрів зв’язку між змінними. Так, як коефіцієнт кореляції наближений до 0, постає питання про статистичну значущість зв’язку між змінними х та у. Тому, перевіримо спочатку коефіцієнт кореляції. При перевірці висуваємо Н0 -гіпотезу - коефіцієнт кореляції генеральної сукупності дорівнює 0 (ƿ=0), Н1- ƿ≠0. Звідси, щоб перевірити Н0 гіпотезу використовуємо розподіл Стьюдента 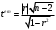 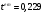 за таблицею Стьюдента при α=0,01, і ступенях свободи 21 визначимо tкр.=2,831. Оскільки tем.< tкр. (0,229 < 2,831), то Н0 приймаємо і з довірчою ймовірністю 99% вважаємо, що коефіцієнт кореляції генеральної сукупності рівний 0, тобто кореляційна залежність між х і у є статистично незначущою. Щоб впевнитися в цьому, необхідно ще перевірити коефіцієнт регресії генеральної сукупності. Для цього висунемо гіпотезу Н0 - β1=0 та Н1- β1≠0. Щоб перевірити статистичну значущість коефіцієнта b1, використовують статистику Стьюдента. Відповідно, за цією формулою 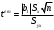 tем.=0,232, за таблицею Стьюдента tкр.= 2,831, при р=0,99 і ступенями свободи 21. Порівнявши tем.< tкр. (0,232 < 2,831), можна прийняти Н0 - β1=0 з довірчою ймовірністю 99%, тобто кореляційний зв’язок між х і у є статистично незначущим. Звідси, можна зробити висновок, що будувати та досліджувати парну кореляційно-регресійну модель для вивчення зв’язку між змінними недоцільно. Експрес-діагностика моделі Для того, щоб швидше перевірити модель на точність і адекватність, деколи використовують експрес-діагностику моделі, яку проводять за допомогою критерію Фішера. Спочатку висуваємо гіпотезу Н0 - коефіцієнт регресії генеральної сукупності (β1=0), потім знаходимо Fем. за з формулою: 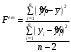 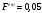 за таблицею Фішера при рівні значущості 0,01, та ступенях свободи (v1=1, v2=21 - якщо значення β1 ближче до 0) знаходимо Fкр.=8,017 і порівнюємо Fем.< Fкр. (0,05 < 8,017). Оскільки Fем. < Fкр., приймаємо гіпотезу Н0- коефіцієнт регресії генеральної сукупності (β1=0), тобто побудована кореляційно-регресійна модель не відповідає дійсності і неадеквано описує кореляційну залежність між змінними х та у. Економічна інтерпретація результатів економетричного дослідження та їх використання Для початку, щоб дослідити зв’язок між факторною ознакою (х) та результуючою ознакою (у) будуємо узагальнену парну лінійну кореляційно-регресійну модель, а на основі її ще й вибіркову. Після цього досліджуємо параметри моделі b1, b0, а також побудували лінію регресії що підтвердила обернений зв’язок між змінними. Дослідили цей зв’язок між змінними за допомогою коефіцієнта кореляції, який підтвердив слабкий та обернений зв’язок між змінними. Автокореляція, яка вийшла в мене додатною, що свідчить про те, що я не зможу отримати ефективні оцінки параметрів методом найменших квадратів. Дослідили адекватність побудови парної лінійної кореляційно-регресійної моделі, дослідили спряжені прямі регресії, а також кут між ними, який вийшов схильним більше до 90 градусів (підтвердження кореляційного слабкого зв’язку між змінними). Перевіривши формулу декомпозиції загальної дисперсії, з’ясували, що непояснена дисперсія результуючої змінної більша за пояснену, що вказує на те, що більшу частину варіації результуючої змінної не може пояснити моя кореляційно-регресійна модель. Це підтвердило емпіричне відношення детермінації, що свідчить про те, що краще вибрати не лінійну, а іншу модель. Ще одним підтвердженням неадекватності моєї парної кореляційно-регресійної моделі була перевірка статистичної значущості параметрів зв’язку між змінними, яка вказала на статистичну незначущість зв’язку між змінними, що і підтвердив експрес-аналіз моделі. Отже, можна зробити висновок, що побудована кореляційно-регресійна модель є неадекватною, її не можна використовувати на практиці, але зв’язок між змінними існує, хоча він і слабкий, тобто потрібно будувати і дослідити іншу модель можливо степеневу або багатофакторну. |
