Обыкновенная дробь. Обыкновенная дробь
 Скачать 0.53 Mb. Скачать 0.53 Mb.
|
ОБЫКНОВЕННАЯ ДРОБЬОдна или несколько равных частей единицы называются обыкновенной дробью. Дробь 3/4 означает, что единицу разделили на 4 части и взяли 3 таких части.  Дробь можно рассматривать и как результат деления натуральных чисел. Частное от деления натуральных чисел а и b можно записать в виде дроби a/b — где делимое а — числитель, а делитель b — знаменатель.  Правильная и неправильная дробь Дробь, в которой числитель меньше знаменателя, называется правильной, а дробь, где числитель больше или равен знаменателю, — неправильной. 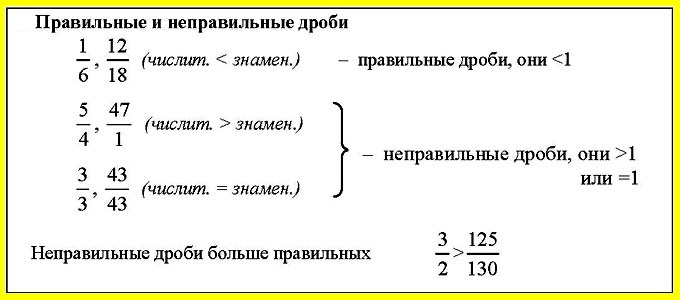 Число, состоящее из целой и дробной частей, можно обратить в неправильную дробь. Для этого нужно умножить целую часть на знаменатель и к произведению прибавить числитель данной дроби. Полученная сумма будет числителем дроби, а знаменателем остается знаменатель дробной части.  Из любой неправильной дроби можно выделить целую часть. Для этого нужно разделить с остатком числитель на знаменатель. Частное от деления — это целая часть, остаток — это числитель, делитель — это знаменатель.  Основное свойство дроби Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной.  Сравнение дробей Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше. Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше. Чтобы сравнить дроби с разными числителями и знаменателями, нужно: привести дроби к наименьшему общему знаменателю; сравнить полученные дроби. Чтобы привести дроби к наименьшему общему знаменателю, нужно: найти наименьшее общее кратное (НОК) знаменателей дробей (оно и будет их общим знаменателем); разделить общий знаменатель на знаменатель данных дробей, т. е. найти для каждой дроби дополнительный множитель; умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.  |
