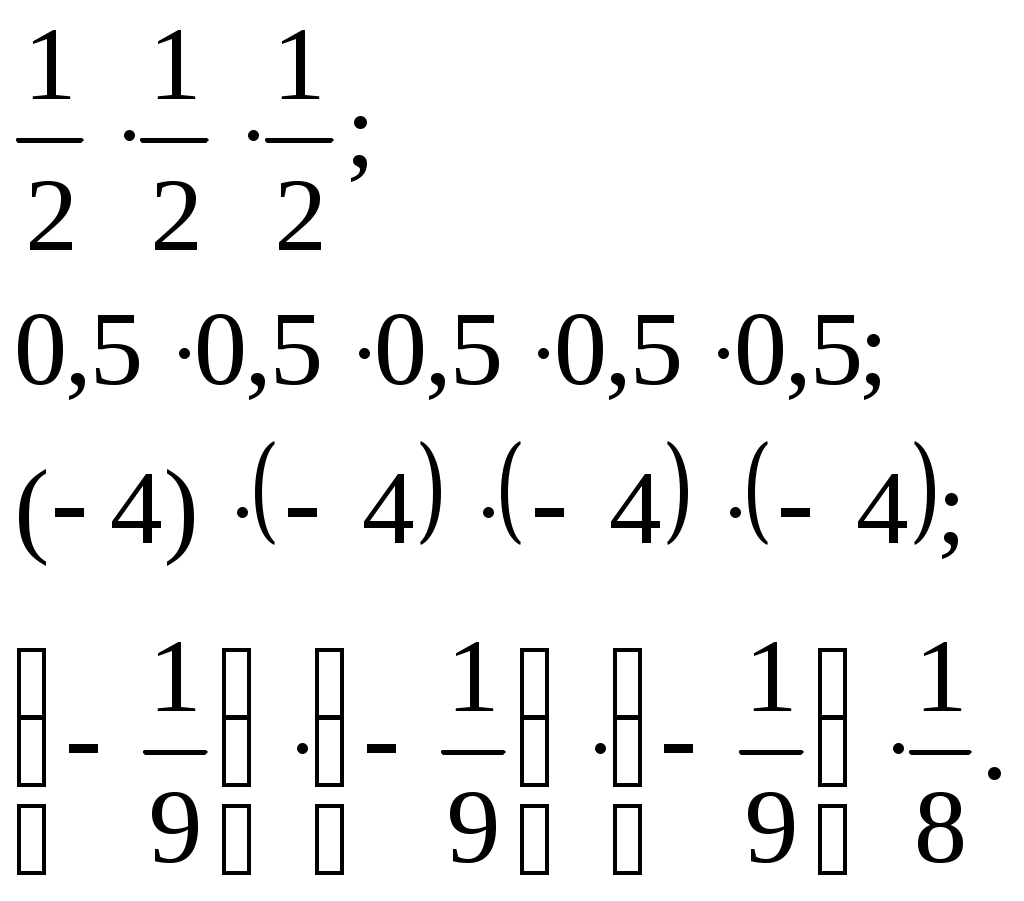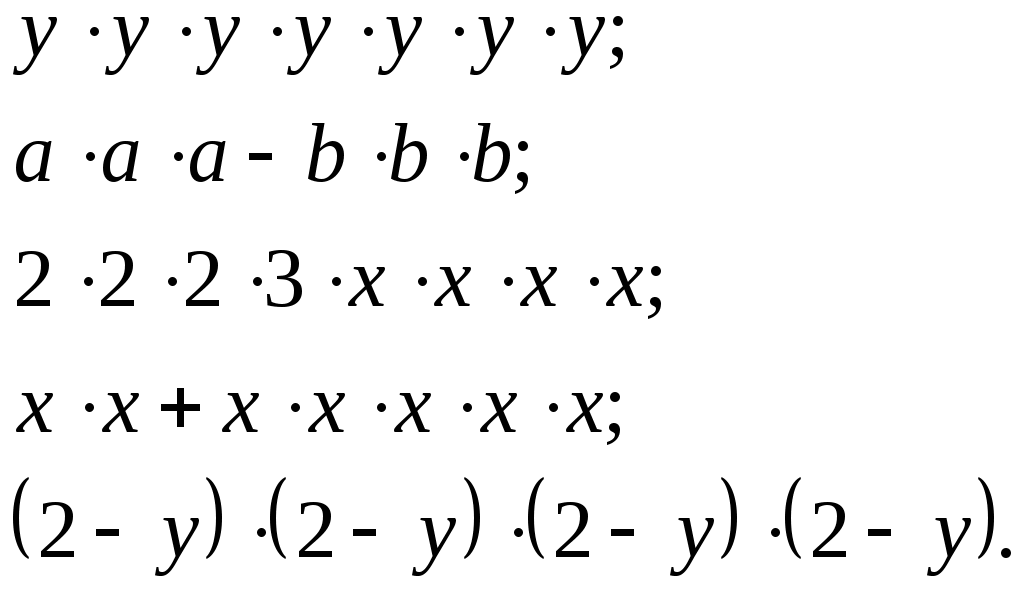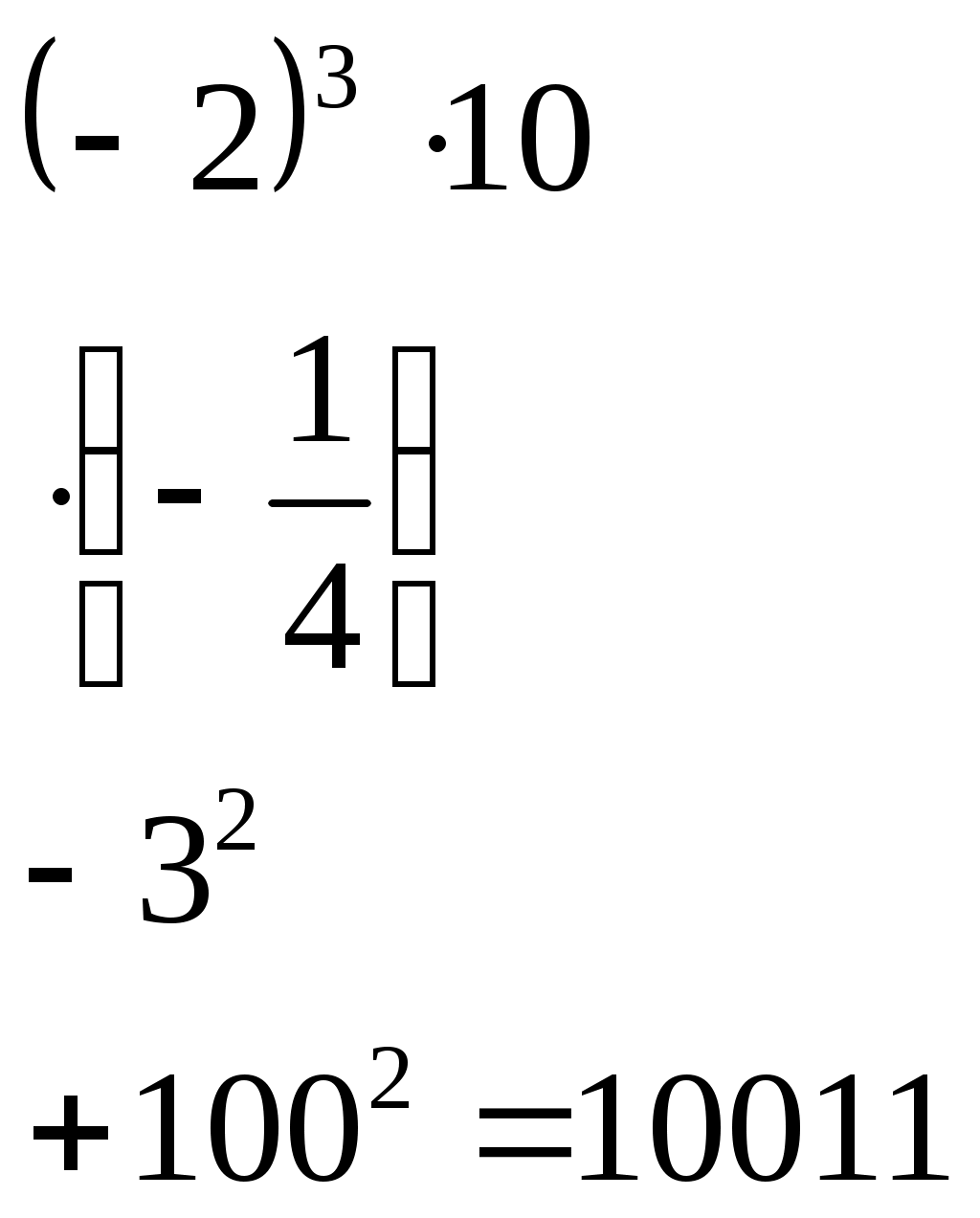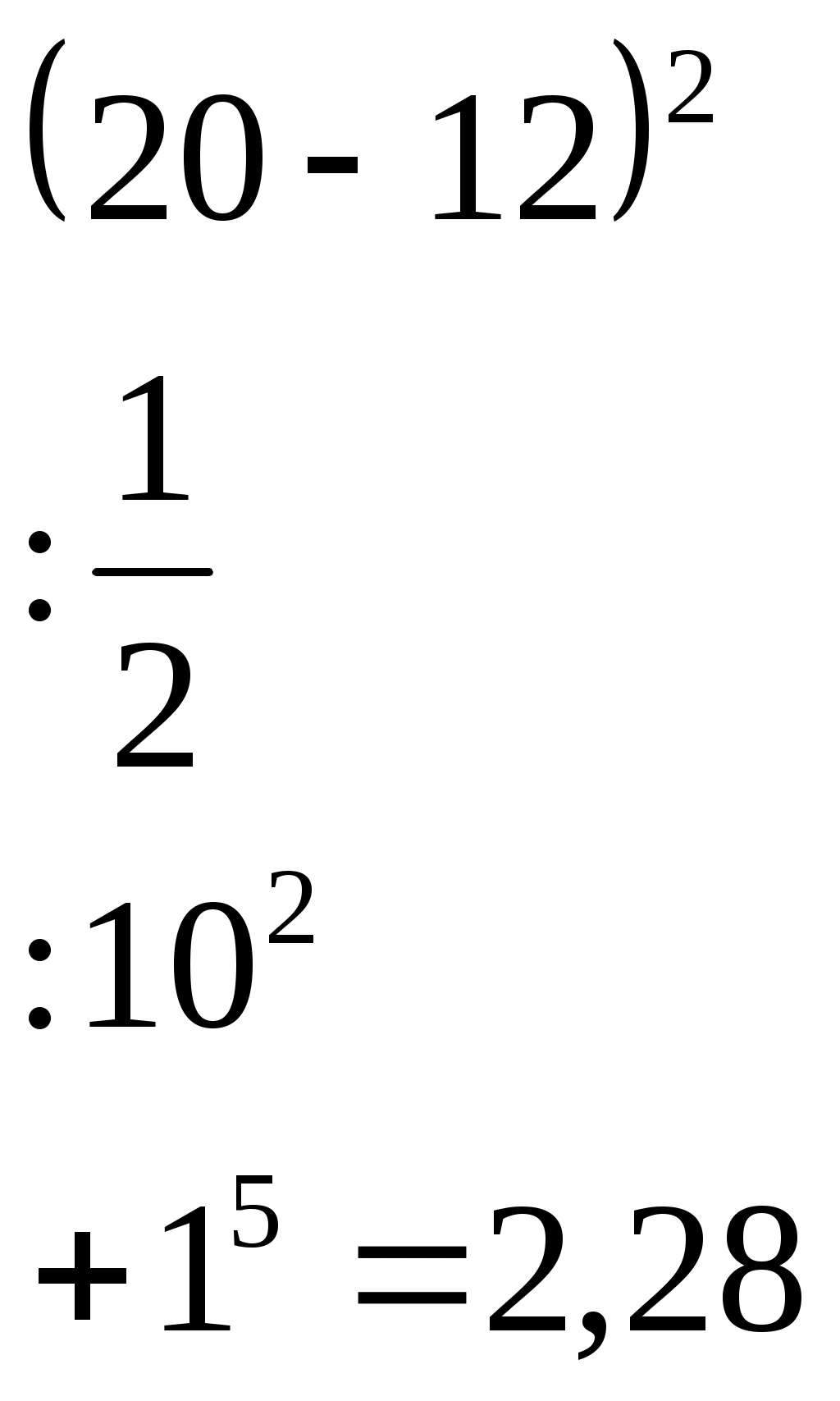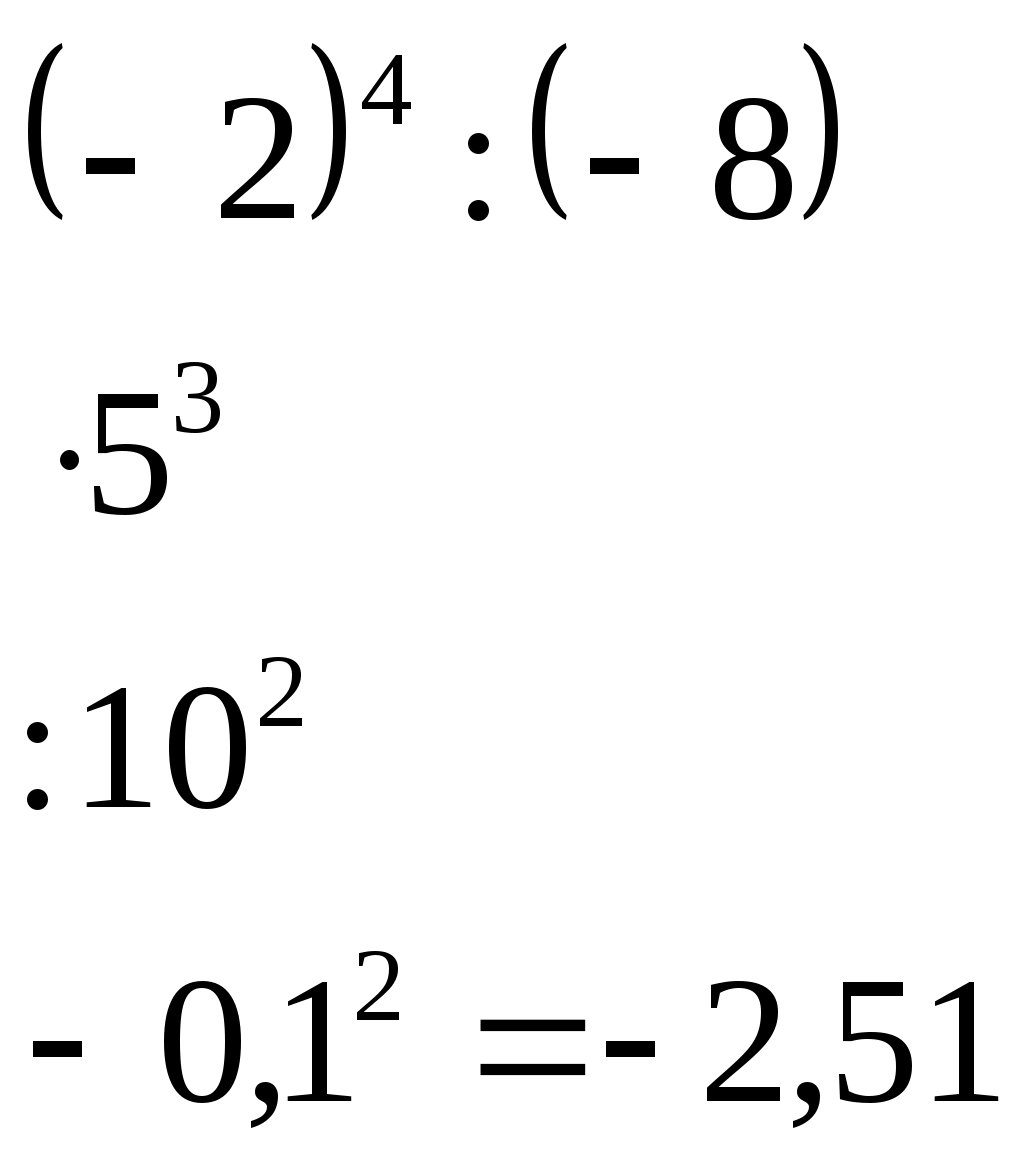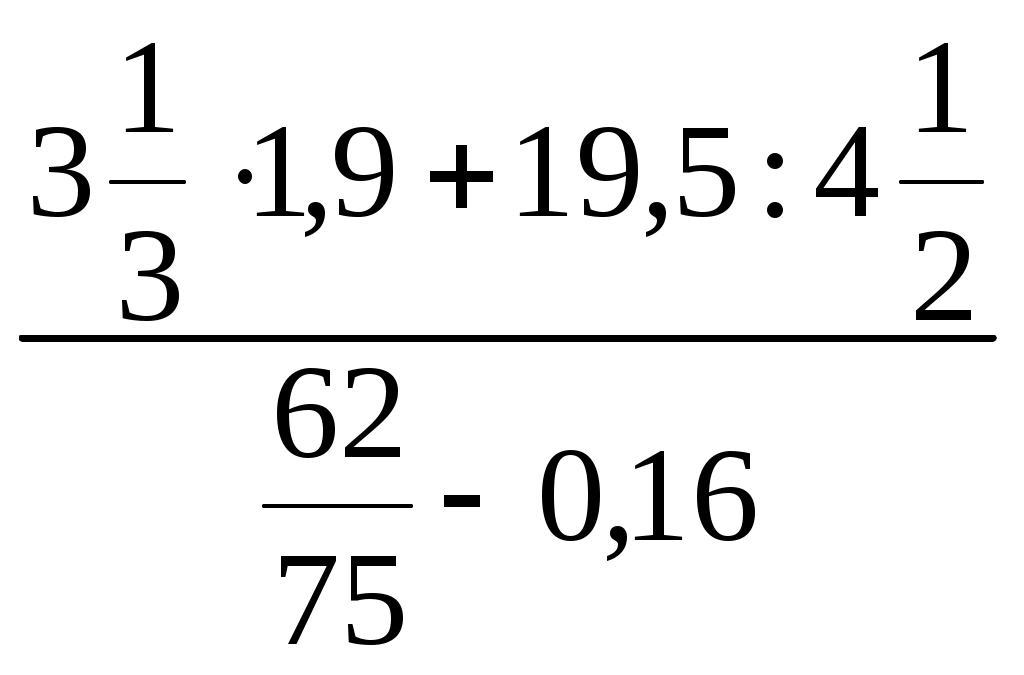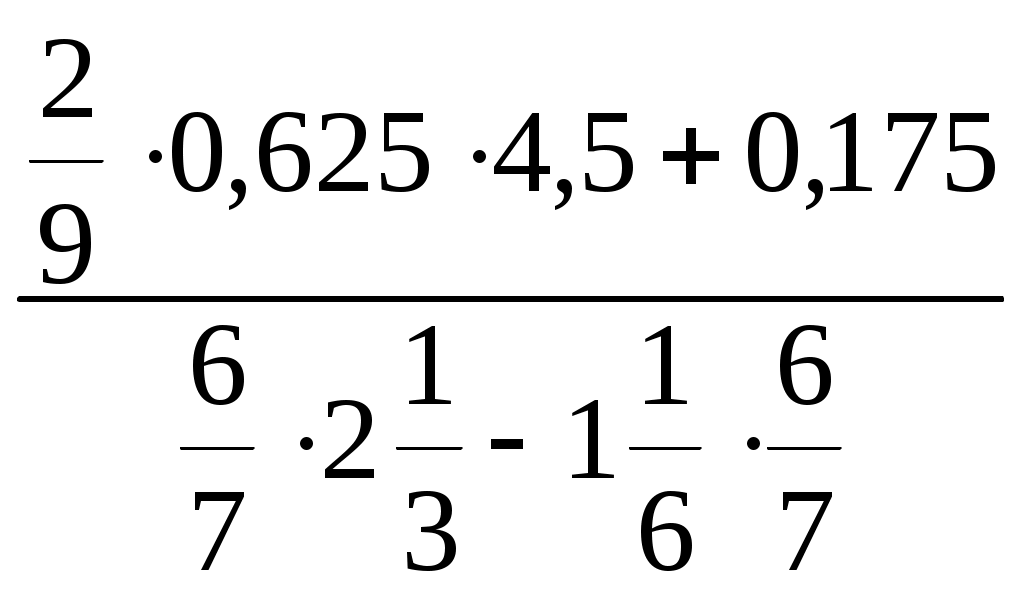конспект урока алгебры в 7 классе. Обыкновенные и десятичные дроби
 Скачать 293.5 Kb.
|
|
Урок 1. Тема: Обыкновенные и десятичные дроби. Цели урока: вспомнить и повторить правила выполнения действий с десятичными и обыкновенными дробями; в течение урока развивать у учащихся навыки решения примеров с обыкновенными и десятичными дробями, а так же вычислительные способности; рассказать об истории развития алгебры и ее ученых. Ход урока: 1. Организационный момент. (3 мин.) 2. Вводная лекция. (5 мин.) Алгебра, вместе с Арифметикой, есть наука о числах и через посредство чисел - о величинах вообще. Не занимаясь изучением свойств каких-нибудь определенных, конкретных величин, обе эти науки исследуют свойства отвлеченных величин, как таковых, независимо от того, к каким конкретным приложениям они способны. Различие между арифметикой и алгеброй состоит в том, что первая наука исследует свойства данных, определенных величин, между тем как алгебра занимается изучением общих величин, значение которых может быть произвольное, а, следовательно, алгебра изучает только те свойства величин, которые общи всем величинам, независимо от их значений. Таким образом, алгебра есть обобщенная арифметика. Это подало повод Ньютону назвать свой трактат об алгебре "Общею Арифметикой". Гамильтон, полагая, что подобно тому, как геометрия изучает свойства пространства, алгебра изучает свойства времени, назвал алгебру "Наукою чистого времени" - название, которое Деморган предлагал изменить в "Исчисление последовательности". Однако такие определения не выражают ни существенных свойств алгебры, ни исторического ее развития. Алгебру можно определить как "науку о количественных соотношениях". Развивали алгебру великие люди, про жизнь некоторых из них можно приготовить доклады. АРХИМЕД (около 287-212 до нашей эры) Архимед получил блестящее образование у своего отца, астронома и математика Фидия, родственника сиракузского тирана Гиерона II, покровительствовавшего Архимеду. В юности провел несколько лет в крупнейшем культурном центре того времени Александрии, где познакомился с Эрастосфеном. Затем до конца жизни жил в Сиракузах. Во время 2-й Пунической войны Архимед организовал инженерную оборону города. Изобретенные им военные метательные и др. машины (о них рассказывает Плутарх в жизнеописании римского полководца Марцелла) в течение двух лет сдерживали осаду Сиракуз римлянами. Архимеду приписывается также сожжение римского флота направленным на него через систему вогнутых зеркал солнечным светом, но это вряд ли достоверно. Гений Архимеда вызывал такое восхищение у римлян, что Марцелл приказал сохранить ему жизнь, но при взятии Сиракуз он был убит не узнавшим его солдатом. Лекция о введении алгебры. Преподаватель должен рассказать о задачах алгебры и ее ученых. Так же надо рассказать о связи алгебры и других предметов. 3. Устный счет. (7 мин.) Устный счет поможет вспомнить правила выполнения действий и развить вычислительные способности. Цепочки с действиями обыкновенных дробей выполняются по действиям, вслух учениками произносится только ответ, причем только один раз. Каждое действие выполняют разные ученики.   Цепочка с десятичными дробями записана на плакате или на доске. Она так же выполняется по действиям. Подставить в эту цепочку можно числа 2,3; 0,7; 1,1.  4. Новый материал. (10 мин.) Провести фронтальный опрос всего класса. Этот опрос поможет вспомнить все возможное о дробях. Как называются члены дроби и что они означают? Какую дробь называют правильной? Неправильной? Расскажите правила перевода неправильной дроби в смешанное число. Расскажите основное свойство дроби. Что значит сократить дробь? Как найти дробь от числа? Расскажите понятие десятичной дроби. Какое свойство десятичных дробей вы знаете? Как перевести десятичную дробь в обыкновенную? Любую ли обыкновенную дробь можно перевести в десятичную? Если ученики не могут вспомнить ответ на какой-либо вопрос, учитель сам отвечает на него и объяснение происходит на доске. Если это, возможно, показывается пример, отвечающий на вопрос. Устно, с полным объяснением разбираются примеры: № 1(а), 2(а, б), 4. 5. Закрепление материала. (15 мин.) Затем на доске и в тетрадях выполняются № 1(б), 2(в). К доске вызываются сразу три ученика, каждый из них выполняет по три примера, а заем объясняет их. После того, как вспомнили все о дробях, класс приступает к решению примеров с дробями. Решаются задания № 6, 7, 10, 34. Для экономии времени на доске выполняются одновременно по 3 – 4 примера (сколько позволяет доска). 6. Подведение итогов. (3 мин.) 7. Домашнее задание. (2 мин.) Прочитать, разобрать и выучить правила из § 1.1. Решить и разобрать задания № 3, 8, 12. Урок 2. Тема: Обыкновенные и десятичные дроби. Цели урока: вспомнить и повторить правила сравнения обыкновенных и десятичных дробей; в течение урока развивать у учащихся навыки решения примеров с обыкновенными и десятичными дробями, сравнения дробей, а так же вычислительные способности. Ход урока: 1. Организационный момент. (2 мин.) 2. Устный счет. (8 мин.) На устный счет даются примеры – цепочки на десятичные дроби.
Так же устно разбираются примеры для развития вычислительной техники № 15, 16, 17. 3. Актуализация знаний. (15 мин.) Чтобы вспомнить и закрепить правила решения примеров с дробями на доске с полным объяснением решаются примеры: № 11, 13. 4. Новый материал. (6 мин.) Вспомнить правила сравнения десятичных дробей. Устно выполнить сравнение № 19. Вспомнить правила сравнения обыкновенных дробей. Устно сравнить дроби:  и   и   и  (Данные примеры можно приготовить на карточках или написать на доске.) 5. Закрепление материала. (10 мин.) Решить и разобрать задания № 29, 21. 6. Подведение итогов. (2 мин.) 7. Домашнее задание. (2 мин.) Прочитать, разобрать и выучить правила из § 1.1. Решить и разобрать задания № 9, 20, 31. Урок 3. Тема: Обыкновенные и десятичные дроби. Цели урока: вспомнить и повторить формулу, связывающую скорость, время и расстояние; показать правила решения и оформления задач на данную формулу; в течение урока развивать у учащихся умение решать задачи и вычислительные способности; проверить умение учеников решать примеры с обыкновенными и десятичными дробями. Ход урока: 1. Организационный момент. (2 мин.) 2. Устный счет. (4 мин.) На устный счет даются примеры – цепочки.    3. Новый материал. (4 мин.) Вспомнить и записать на доске формулу  и все формулы, вытекающие из нее.Затем с помощью нее решить устно задачи. Машина едет со скорость 80 км/ч. Сколько километров она проедет за 3 часа? За 10 часов? За 30 минут? Велосипедист едет со скоростью 30 км/ч. Сколько времени ему потребуется, чтобы проехать 180 км? 300 км? 10 км? № 24 из учебника. 4. Закрепление материала. (21 мин.) Решить и разобрать задания № 26, 39, 30, 32, 36. 5. Самостоятельная работа. (10 мин.)
6. Подведение итогов. (2 мин.) 7. Домашнее задание. (2 мин.) Прочитать, разобрать и выучить правила из § 1.1. Решить задания № 14, 22, 23, 28. Урок 4. Тема: Степень с натуральным показателем. Цели урока: объяснить понятие степени и правила вычисления степени с натуральным показателем; в течение урока развивать у учащихся навыки вычисления степеней и решения примеров с использованием степени; рассмотреть задания повышенной трудности с использованием степени. Ход урока: 1. Организационный момент. (2 мин.) 2. Анализ самостоятельной работы. (5 мин.) Выставить оценки за самостоятельную работу. Если в самостоятельной работе были повторяющиеся ошибки, разобрать их. Для закрепления данной темы, решить пример. На доске пример решается по действиям (разные действия – разные ученики). 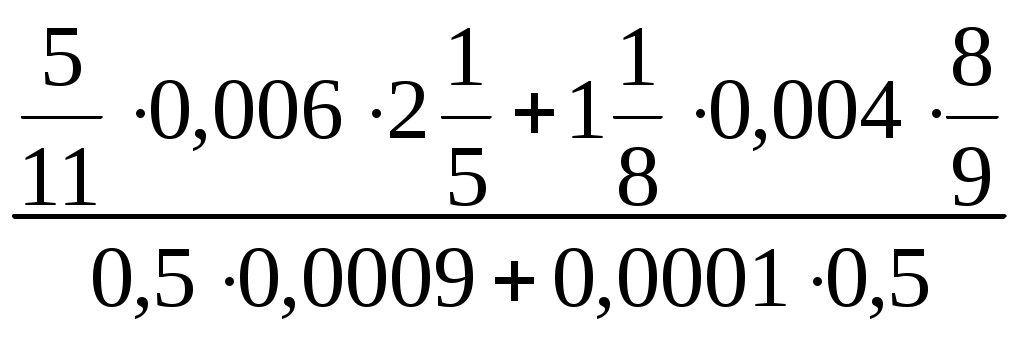 3. Новый материал. (8 мин.) Дать определение степени. С помощью определения, ученики должны найти верное равенство и объяснить ответ.     Также устно, с полным объяснением, вычислить:  4. Закрепление материала. (25 мин.) Решить № 43, 45 (на доске записываются только ответы), 44 (устно), 48, 64. На доске рассмотреть пример по записи степени. Объяснить данную запись и смысл данного выражения. 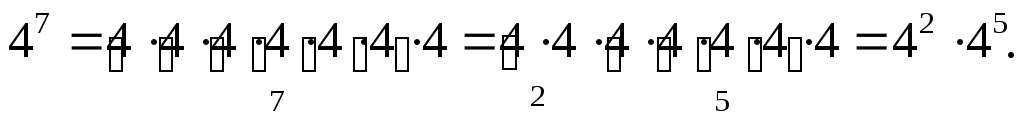 Тут же предложить учащимся представить данную степень в виде произведения двух других степеней с основанием 4. После решить № 55, 56, 57 (устно). 5. Подведение итогов. (3 мин.) 6. Домашнее задание. (2 мин.) Прочитать, разобрать и выучить правила из § 1.2. Решить задания № 47, 58, 42. Урок 5. Тема: Степень с натуральным показателем. Цели урока: объяснить правила возведения в степень отрицательных чисел; в течение урока развивать у учащихся навыки вычисления степеней и решения примеров с использованием степени; показать правила нахождения последней цифры результата, не выполняя вычислений. Ход урока: 1. Организационный момент. (2 мин.) 2. Индивидуальный опрос. (4 мин.) Двое учеников вызываются к доске, на которой заранее записаны задания по упрощению выражений:
Пока двое учеников выполняют задание, остальные устно вычисляют:  После проверяются примеры на доске. 3. Актуализация знаний. (5 мин.) Для закрепления понятия степени решаются примеры № 49. 4. Новый материал. (7 мин.) Устно выполняется № 51. А на доске еще остались примеры из № 49. По этим двум номерам разбирается, что происходит с отрицательными числами в четной степени и в нечетной степени. Так же разбирается, почему четная степень делает число положительным, а нечетная степень отрицательное число оставляет отрицательным. 5. Закрепление материала. (22 мин.) Для закрепления материала устно, с полным объяснением, разбирается № 50. После выполняются на доске и в тетрадях задания № 52, 65, 66, 67, 59, 60, 72. Разобрать следующее задание: Не вычисляя выражения, найти цифру, на которую заканчивается результат данного действия.  6. Подведение итогов. (3 мин.) 7. Домашнее задание. (2 мин.) Прочитать, разобрать и выучить правила из § 1.2. Решить задания № 68, 53, 54, 71. Урок 6. Тема: Решение задач на проценты. Цели урока: в течение урока развивать у учащихся вычислительные способности с использованием степени; объяснить понятие процентов; вспомнить и повторить правила решения и оформления задач на проценты; рассмотреть задачи – шутки с процентами для повышения интереса к математике. Ход урока: 1. Организационный момент. (2 мин.) 2. Устный счет. (4 мин.)
3. Новый материал. (12 мин.) Вспомнить понятие и обозначение процентов, правила перевода десятичных дробей в проценты и обратно. Вспомнить правила оформления и решения задач на проценты, решив следующую задачу. Мама купила 2 кг. 400 г. конфет. Известно, что 30% всех конфет – шоколадные конфеты. Сколько шоколадных конфет купила мама? Эта задача рассматривается на доске. И тут же из нее можно сделать и разобрать следующие задачи. Мама купила 720 г. шоколадных конфет. Известно, что они составляют 30% всех конфет. Сколько килограмм конфет купила мама? Мама купила 2 кг. 400 г. конфет. Известно, что из них 720 г. шоколадных конфет. Сколько процентов составляют шоколадные конфеты от общего количества? 4. Закрепление материала. (22 мин.) Для закрепления материала устно, с полным объяснением, разбирается № 74, 75. После выполняются на доске и в тетрадях задачи № 76, 79, 81, 83. Затем № 86 выполняется по рядам. Первый ряд (а), второй ряд (б), третий ряд (в). Дается некоторое время на обдумывание, затем кто-то с ряда показывает решение на доске. Рассмотреть решение следующих задач. 1) Малыш полетел к Карлесону в гости. Когда они пролетели 56 м, что составило 70% всего расстояния, моторчик заглох. Сколько метром еще им осталось пролететь до дома Карлесона? 2) В школе добросовестно учатся 430 учеников, а еще 70 валяют дурака. Какой процент учеников школы валяют дурака? 3) Коля и Толя закопали свои дневники, Коля на глубину 10 метров, а Толя – 12 метров. Археологи далекого будущего когда-нибудь раскопают оба окаменевших дневника с большим количеством окаменевших двоек. В Колином дневнике они найдут 224 двойки, а в Толином 25% этих двоек. Сколько всего двоек найдут археологи в окаменевших дневниках? 5. Подведение итогов. (3 мин.) 6. Домашнее задание. (2 мин.) Прочитать, разобрать и выучить правила из § 1.3. Решить задания № 68, 53, 54, 71. Урок 7. Тема: Решение задач на проценты. Цели урока: проверить знания и умения по работе с процентами, степенями и дробями; в течение урока развивать у учащихся вычислительные способности с использованием степени, дробей и процентов; так же развивать у учеников навыки решения и оформления задач на проценты; рассмотреть задачи – шутки с процентами для повышения интереса к математике. Ход урока: 1. Организационный момент. (2 мин.) 2. Математический диктант. (8 мин.)
Ученики меняются тетрадями и под диктовку учителя проверяют ответы и ставят оценки. После разбираются ошибки. 3. Устная работа. (10 мин.) Затем устно разбираются № 78, 87, 88, 85. 4. Решение задач. (10 мин.) Решаются на доске № 92, 94. Также решить следующую задачу: 40 бабушек вошли в автобус. 70% бабушек купили билеты, а остальные закричали, что у них проездной билет. Контролер проверил. На самом деле оказалось, что проездной только у 7 бабушек. Сколько бабушек ехало «зайцами»? 5. Самостоятельная работа. (10 мин.)
6. Подведение итогов. (3 мин.) 7. Домашнее задание. (2 мин.) Прочитать, разобрать и выучить правила из § 1.3. Решить задания № 84, 91, 93. Урок 8. Тема: Решение задач на проценты. Цели урока: проверить умение учеников решать задачи на проценты и решать примеры с дробями; в течение урока развивать у учащихся навык решения и оформления задач на проценты; рассмотреть задачи – шутки с процентами для повышения интереса к математике. Ход урока: 1. Организационный момент. (2 мин.) 2. Анализ самостоятельной работы. (3 мин.) Выставить оценки за самостоятельную работу. Если какие-то ошибки повторялись, то их разобрать на доске. 3. Индивидуальный опрос. (12 мин.) Из тех учеников, кто плохо написал самостоятельную работу, вызвать к доске четырех человек, на работу с карточкой. А остальные в этот момент решают в тетрадях № 97.
На решение дается 5 – 7 минут, после чего проверяются задачи, решенные на доске, а затем проверяется устно № 97. 4. Решение задач. (17 мин.) Решение задач на проценты из второй главы можно провести следующим образом. На доске выписать номера, а ученики в тетрадях решают задачи из данных на выбор. После 10 минут решения, к доске вызвать пятерых учеников (если доска не позволяет, сначала троих, а затем еще двоих), которые решили соответствующие задачи. На запись дается 3 – 5 минут, после чего каждый объясняет свою задачу (и получает оценку). Преподаватель может в этот момент взять тетради у тех, кто за это время решил 2 или 3 задачи, и выставить им оценки. Сидящие проверяют свои записи и дополняют их. Решить № 101, 102, 104, 106, 107. Если осталось время, совместными усилиями класса разобрать решение задачи: Хор, состоящий из 280 мальчиков и 105 девочек, исполняет задушевную песню. К счастью, лишь 25% мальчиков и третья часть девочек орет во все горло, а остальные только открывают рот. Сколько процентов составляют орущие девочки от орущих мальчиков? 5. Закрепление – тестирование. (6 мин.) Для закрепления пройденного материала и проверки усвоенного тестирование из трех заданий. Записать можно на доске. Каждый выполняет самостоятельно в тетради. После 6 минут решения проверяются ответы, если какое-то задание не выполнили большинство учеников, то это задание разбирается на доске. 1. Найти произведение чисел, обратных к числам  и  .1)  2) 1; 3)  4) 2; 5)  2. Чему равно значение выражения  ?1) 1; 2) 1,6; 3)  4) 0,6; 5)  3. В аудитории, где проходит экзамен, 56% - девочки, остальные мальчики. Среди приведенных чисел выберете то, которое может быть числом абитуриентов в этой аудитории. 1) 44; 2) 60; 3) 80; 4) 99; 5) 50. ОТВЕТЫ: 1 – 1, 2 – 5, 3 – 5. 6. Подведение итогов. (3 мин.) 7. Домашнее задание. (2 мин.) Прочитать, разобрать и выучить правила из § 1.3. Решить задания № 100, 105, 95. Урок 9. Тема: Статистические характеристики. Цели урока: объяснить понятие ряда; ввести понятия среднего арифметического, размаха и моды ряда; рассказать о науке – статистике и ее применении в жизни; рассмотреть наглядное применение статистики в повседневной жизни. В течение урока развивать у учащихся навык нахождения статистических характеристик, умение обучаться самостоятельно. А так же в течение урока воспитывать в детях чувство сотрудничества. Ход урока: 1. Организационный момент. (2 мин.) Для изучения данной темы требуется возможность обсуждения, поэтому урок проводится в групповой форме. Учеников рассадить в группы по 5 человек. 2. Новый материал. (13 мин.) Статистика – наука, которая занимается получением, обработкой и анализом количественных данных о разнообразных массовых явлениях, происходящих в природе и обществе. Слово «статистика» происходит от латинского слова  , которое означает «состояние, положение вещей». Статистика изучает численность отдельных групп населения страны и ее регионов, производство и потребление разнообразных видов продукции, перевозку грузов и пассажиров различными видами транспорта, природные ресурсы и многое другое. Результаты статистических исследований широко используются для практических и научных выводов. В настоящее время статистика начинает изучаться уже в средней школе, в ВУЗах это обязательный предмет, потому что связан со многими науками и отраслями. Чтобы увеличить количество продаж в магазине, чтобы улучшить качество знаний в школе, чтобы двигать страну по экономическому росту, надо проводить статистические исследования и делать соответствующие выводы. И это должен уметь каждый.Затем надо прочитать задачу и опросить учеников, что они могут сказать и какие выводы сделать. Для начала дать группам самостоятельно это обсудить, а затем выслушать нескольких человек и обсудить услышанное. В институте сдавали зачет по высшей математике. В группе было 10 человек, и они получили соответствующие оценки: 3, 5, 5, 4, 4, 4, 3, 2, 4, 5. Можно задать следующие вопросы. Какую оценку получали чаще всего? Как в целом сдала группа? Насколько разные были оценки? После обсуждения с учениками, дать время на прочтение параграфа данной темы. Ученики должны в группе прочесть данный материал и ввести понятие ряда и характеристик ряда. Дать определения статистическим характеристикам ряда, объяснить их значение и вычислить их для данного ряда. Затем сверяются ответы и если что-то ученики поняли или вычислили не верно, то преподаватель исправляет и объясняет. 3. Закрепление нового материала. (10 мин.) Для закрепления устно выполнить № 111. Затем для каждой группы на карточках раздать ряд чисел, для которого надо найти среднее арифметическое, размах ряда и моду.
С каждой группы по одному ученику должны показать решение своего задания у доски и объяснить его всему классу. Письменно всеми учениками решаются задания № 118, 119, объяснение решения и оформления должны быть на доске. 4. Статистическое исследование. (15 мин.) Затем предложить ученикам каждой группы провести исследование, оно у всех групп одинаковое, но оформить лучше на карточках. В женском обувном магазине провели статистические исследования и составили соответствующую таблицу по цене обуви и количества продаж:
Для данных показателей надо найти статистические характеристики и объяснить их значение. После ученики должны ответить на следующие вопросы: Из данных ценовых категорий, обувь за какую цену не следует продавать магазину? Обувь, по какой цене следует распространять? К какой цене лучше стремиться? По каким параметрам еще можно провести статистические исследования в обувном магазине? Приведите еще наглядные примеры использования статистики. 5. Подведение итогов. (3 мин.) 6. Домашнее задание. (2 мин.) Прочитать, разобрать и выучить правила из § 1.4. Решить задания № 110, 114, 116, 108. Урок 10. Тема: Статистические характеристики. Цели урока: объяснить правила построения столбчатых и круговых диаграмм; рассмотреть решение задач по статистике повышенной трудности; проверить умение находить статистические характеристики. В течение урока развивать у учащихся навык нахождения статистических характеристик и умение строить диаграммы различных видов. Ход урока: 1. Организационный момент. (2 мин.) 2. Индивидуальный опрос. (10 мин.) К доске вызвать трех учеников, для работы по карточкам.
Остальные в этот момент решают в тетрадях задание № 121. На решение дается 5 минут, после чего проверяются задачи на доске. После проверки задач ученики сравнивают результаты участников из 2-ой и 3-ей карточек, выясняя, кто из участников победил и по какой характеристике лучше судить соревнования. Затем проверяется устно задание № 121. 3. Новый материал. (10 мин.) После работы с диаграммой из задания № 121, обсудить правила построения столбчатой диаграммы и построить совместными усилиями на доске и в тетрадях диаграмму по условию задачи. В течении двух кварталов отмечалось посещение бассейна по месяцам: январь – 685 человек, февраль – 790 человек, март – 1005 человек, апрель – 1560 человек, май – 1000 человек, июнь – 2545. Затем объяснить правила построения круговой диаграммы и построить на доске такого вида диаграмму по условию задачи. В классе 36 человек, из них 20 человек – хорошисты, 5 – отличники, а остальные троечники. Сравнить два вида диаграмм, и обсудить когда и какого вида диаграммы применяются. 4. Решение задач. (18 мин.) Решить задачи – исследования и сделать соответствующие выводы по заданиям № 122, 123, 124. Так же разобрать следующие задачи: 1) В ряду чисел  пропущено одно число. Найдите его, если среднее арифметическое ряда равно 20; если размах ряда равен 30; мода ряда равна 8.2) Относительно трех чисел известно, что среднее арифметическое первых двух равно 25, а среднее арифметическое всех трех чисел – 30. Чему равно третье число? 3) Задачи № 120, 115. 5. Подведение итогов. (3 мин.) 6. Домашнее задание. (2 мин.) Ответить на вопросы для повторения к главе, письменно ответить на вопросы 3, 4, 5, 6. Решить задание № 119 (построить два вида диаграмм). Урок 11. Тема: Подготовка к контрольной работе. Цели урока: повторить и закрепить понятия степени, процентов, определения статистических характеристик; подготовиться к контрольной работе; проверить готовность к контрольной работе. В течение урока развивать у учащихся навык решения задания по пройденным темам. Ход урока: 1. Организационный момент. (2 мин.) Рассадить детей на 4 группы. Рассказать тему и цели урока. 2. Актуализация знаний. (8 мин.) В группах письменно отвечают на вопросы из заданий для самопроверки: 1, 2, 3, 4, 5, 8, 10, 11. Решение должно быть у каждого в тетради, и каждый должен знать объяснение заданий. На выполнение дается 7 минут. После чего все задания проверяются устно, при этом отвечающие должны ответить на следующие вопросы: Как переводить десятичную дробь в обыкновенную? Как переводить обыкновенную дробь в десятичную? Любую ли дробь можно перевести в десятичную? Расскажите алгоритм сравнения обыкновенных дробей. Как сравнить десятичные дроби? Что значит порядок возрастания? Убывания? Расскажите понятие степени с натуральным показателем. Как перевести десятичную дробь в проценты? Как проценты представить десятичной дробью? 3. Закрепление материала. (10 мин.) Каждой группе раздается карточка, задания которой выполняют в группе совместно. Затем по ответам, соответствующим ответам буквам и номеру задания составляется на доске фраза. Должно получиться «Математика – царица наук». Если какая-либо буква найдена не верно и фраза не составляется, то задание под этим номером рассматривается на доске всем классом.
4. Проверка – тестирование. (6 мин.) Тесты можно оформить на карточках, для каждой группы по одной. Решать данные задания ученики должны самостоятельно. Решение проверяется по ответам. Если у нескольких учеников вызвало затруднение какое-нибудь задание, оно разбирается на доске и дается время на обсуждение его в группе. 1. Вычислите  .1) 6,84; 2) 5,82; 3) – 6,84; 4) – 5,82; 5) 5,84. 2. В 140 грамм воды добавили 60 г соли. Сколько процентов соли в этом соленом растворе? 1) 20; 2) 30; 3) 25; 4) 35; 5) 45. 3. Среднее арифметическое трех чисел равно 10, а среднее арифметическое двух других 15. Найдите среднее арифметическое этих пяти чисел. 1) 10; 2) 11; 3) 12; 4) 13; 5) 14. ОТВЕТЫ: 1 – 3, 2 – 2, 3 – 3. 5. Решение задач. (14 мин.) Преподаватель объяснят решение и правила оформления задания № 129. Затем дается каждой группе один из номеров задач № 125, 126, 127, 128 и на решение 5 минут. Те группы, которые справились со своей задачей, выдвигают одного из учеников для объяснения задачи на доске. Если какая-то группа не справилась с задачей, она дается им для домашнего решения. И во время анализа контрольной работы им дается возможность объяснить и показать ее решение. Если же ученики и дома не справятся с задачей, то сам преподаватель объясняет ее решение. 6. Подведение итогов. (3 мин.) 7. Домашнее задание. (2 мин.) Решить задания № 7, 9, 13, 15 (стр. 35 – 36), задачу №126. Урок 12. Контрольная работа. Цели урока: проверить знания учеников по данной теме. Ход урока: 1. Организационный момент. 2. Контрольная работа. Вариант 1. 1. Найти значения выражений: а)  б)  в)  2. Сравнить числа: а)  и  б)  и  ; в)  и  .3. Боря потратил 5% своих денег. Сколько было у Бори денег, если после того, как он их потратил, у него осталось 160 рублей? 4. На празднике 75% цветов были розы, а остальные 224 цветка – георгины. Сколько всего цветов было на празднике? 5. Найдите среднее арифметическое значение, моду и размах ряда: 15, 121, - 61, 121, 0, 20. Вариант 2. 1. Найти значения выражений: а)  б)  в)  2. Сравнить числа: а)  и  б)  и  ; в)  и  .3. Количество деревьев в саду в мае выросло на 4%. Сколько деревьев стало в саду, если в апреле их было 650? 4. 65% шаров на празднике были красными. А остальные 175 – зелеными. Сколько всего шаров было на празднике? 5. Найдите среднее арифметическое значение, моду и размах ряда: 35, - 23, 121, - 55, 35, - 35. 3. Домашнее задание. Решить задания № 130, 131. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
?
или 
?
или 2,57?