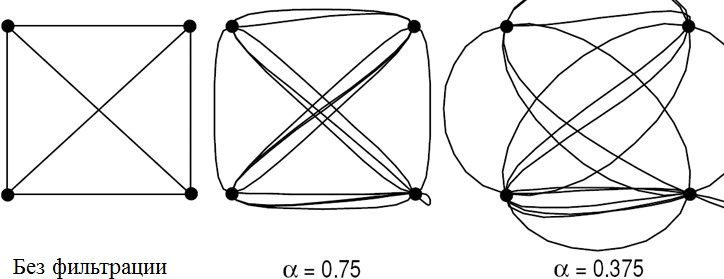
Области применения, виды принимаемых сигналов и задачи упос
 Скачать 1.37 Mb.
|
Особенности цифровых УПОСМежсимвольная интерференция. Причины возникновения и методы борьбы сней.В любой системе имеет место естественное или преднамеренное ограничение диапазона частот сверху. Это приводит к межсимвольной интерференции (МИ).  До какого предела можно уменьшать полосу пропускания канала, чтобы МИ не приводила ошибкам? По Найквисту наименьшая верхняя граничная частота полосы пропускания, при которой возможно отсутствие межсимвольной интерференции: fв = 1/(2T). МИ отсутствует, если передаточная функция системы прямоугольная, а импульсная характеристика имеет вид синка. Но длительные осцилляции у синка приводят к тому, что при наличии неравномерности АЧХ тракта или взятии отсчетов не в соответствующие моменты времени МИ появляется вновь. Поэтому хорошо иметь импульсную характеристику с меньшими осцилляциями (в частотной области этому соответствует сглаженный переход АЧХ в область задерживания). 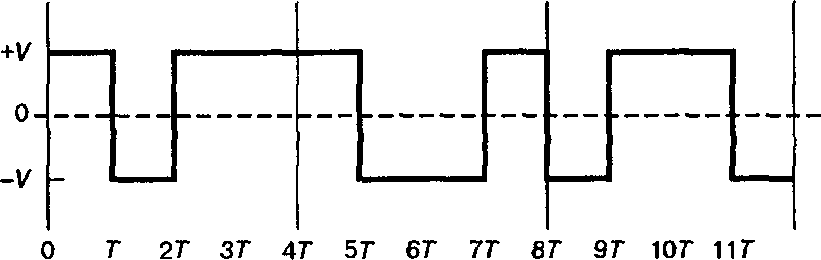Фильтры Найквиста. Приподнятыйкосинус.МИ отсутствует также при любой другой форме импульсной характеристики тракта приема- передачи, если она имеет нули в моменты времени, отстоящие на тактовый интервал от момента передачи текущего символа. Такая импульсная характеристика получается в том случае, если синк умножить на любую другую функцию. Данные импульсы называются импульсами Найквиста. Ясно, что их существует бесконечное количество. Устройства, имеющие импульсную характеристику в виде импульса Найквиста, называются фильтрами Найквиста. Их также существует бесконечное количество.  Если синк домножить на , то получим разновидность  фильтра Найквиста, которая называется «приподнятый косинус». Здесь fs– частота следования символов. Реализация фильтров Найквиста в УПОС с канальным кодированием «без возвращения к нулю». На вход компаратора в приемнике должны поступать сигналы, имеющие форму импульсов Найквиста. Такой сигнал получается, если на вход фильтра Найквиста подать дельта-функцию (сигнал с равномерным спектром). Бывает, что подлежащий передаче цифровой поток в передатчике формируется с кодом канала NRZ (Non Return to Zero, без возвращения к нулю).В такой системе символизирующий определенный бит видеоимпульс длительностью T имеет собственный спектр X(f) = sin(pfT)/(pfT). Чтобы в этом случае на выходе фильтра получить импульсы Найквиста, нужно домножить передаточную функцию фильтра Найквиста на обратную функцию (pfT)/sin(pfT). 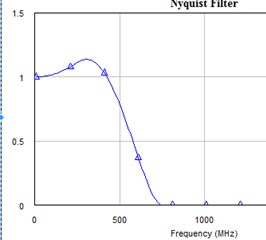 Pulse: входной сигнал – видеоимпульсы длительностью в тактовый интервал (код NRZ)Распределение передаточной функции фильтра Найквиста между приемникоми передатчиком.Передаточной функции фильтра Найквиста должна соответствовать сквозная передаточная функция тракта «передатчик – приемник» H(f) = Ht(f)Hr(f). (1) Фильтрация в передатчике уменьшает излучение за пределами отведенной полосы частот и уменьшает помехи другим приемникам. Фильтрация в приемнике уменьшает проникновение широкополосного шума на вход приемника и помехи от других передатчиков. Известно, что наибольшее отношение сигнал/шум на выходе приемника получается в том случае, когда передаточная функция приемника Hr(f) является комплексно сопряженной функцией по отношению к спектру входного сигнала приемника, который определяется передаточной функцией передатчика Ht(f). Другими словами, должно выполнятся условие Hr(f) = Ht(f)*. С учетом того, что фильтр Найквиста имеет ФЧХ тождественно равную нулю Hr(f) = Ht(f). Подставив последнюю формулу в (1) получим, что H(f) = Ht2(f). Отсюда следует, что передаточная функция передатчика должна быть. Такой же должна быть и передаточная функция приемника. Ht f  H fИспользование фильтров Гаусса и Чебышева в тракте основной селекции цифровых УПОС. В стандарте GSM вместо фильтра Найквиста используется фильтр Гаусса. Это связано с его преимуществами по мощности несущей, занимаемому диапазону и восстановлению тактового сигнала. Импульсная характеристика фильтра Гаусса описывается выражением: h( tT)  t 2 1 0.5 ht exp h( t) |