TПИКСиС Доклад. Обозначения и сокращения
 Скачать 0.49 Mb. Скачать 0.49 Mb.
|
ОБОЗНАЧЕНИЯ И СОКРАЩЕНИЯАССипД – абонентские системы связи и передачи данных; ОЦК – основной цифровой канал; СПД – система передачи данных; ЦПС – цифровая первичная сеть; ЦСС – цифровые системы связи; SDH – Synchronous Digital Hierarchy – синхронная цифровая иерархия; ТDM – Time Division Multiplexing – временное мультиплексирование. -Статические и динамические модели сетей различной топологии1 Сетевой трафик в системах связи1.1 Общие характеристики сетевого трафика Основные информационно-технические характеристики транспортной или корпоративной сети, которые определяют возможности по предоставлению гарантированного качества услуг для пользователей и работоспособности сети в целом, обычно задают на этапе планирования и уточняют в результате проектирования и оптимизации сети. К ним относятся: – пропускная способность транспортных магистралей или базовые скорости передачи; – объем входящего и исходящего трафиков в сетевых узлах; – суммарный трафик в сетевых трактах и магистралях сети; – надежность или коэффициент готовности сети в целом. Технически обоснованный подход к выбору сетевых технологий и архитектуры построения мультисервисных сетей опирается на анализ трафика в сети и оценку пропускной способности транспортных сетей в зависимости от загрузки магистральных каналов сети и соотношения долей основных типов трафика (голос/данные). На основе оценки пропускной способности магистральных сетей и анализа трафика ЦСС можно планировать ее реальную загрузку. Значительный рост объема трафика в ЦСС в последние годы привел к пересмотру требований, предъявляемых к магистралям цифровых транспортных сетей. Появились приложения, которые требуют таких новейших сетевых услуг, как видеосвязь, системы управления распределенными базами данных, что, в свою очередь, требует соответствующего уровня защиты и поддержки качества обслуживания. Современные ЦСС позволяют передавать и коммутировать различные виды трафика со скоростями до 10 Гбит/с и выше. В ЦСС выделяют две основные категории трафика – трафик реального времени (передача голоса, аудио, видео и т.п.) и трафик передачи данных. Условно трафик передачи данных делится на три категории, отличающиеся друг от друга требованиями к временным задержкам при передаче. Трафик реального времени – трафик с аудио- и видеоинформацией, практически не допускающий задержек. Для такого трафика допустимая задержка постоянна и обычно не превышает 0,1 с. Трафик транзакций, в котором допустимая временная задержка не должна превышать 1 с. Большие задержки приводят к снижению производительности труда в работе. Трафик данных, где допустима любая временная задержка, вплоть до нескольких секунд. Особенностью такого трафика является повышенная чувствительность к доступной пропускной способности сети, а не к временным задержкам. При увеличении пропускной способности сети уменьшается время передачи данных. Приложения, требующие передачи больших объемов данных, обычно занимают всю доступную полосу пропускания сети. По характеру передаваемой информации основными видами трафика являются: – передача голоса; – передача данных; – передача видеотрафика; – передача мультимедиа (аудио, видео, данные). Голосовой и видеотрафик – это трафики реального времени, поэтому они предъявляют жесткие требования к необходимой полосе пропускания и временным задержкам в канале связи. Например, для качественной передачи голоса требуется ОЦК Е0 со скоростью передачи 64 кбит/с. Для высококачественной передачи музыки требуется полоса частот от 16 кГц и выше, что соответствует скорости передачи в ЦСС 128 кбит/с. В системах видеоконференций передается только разность между двумя последующими кадрами. В обычной ситуации, когда наблюдаемый объект совершает небольшие движения, объем данных, которые необходимо передать, может составлять только 1 % объема полного кадра, т.е. 1,28 Мбит/с. Если изображение обновляется нечасто и применяются методы сжатия видеосигнала, то для передачи сигналов видеоконференций и получения хорошего качества видеоизображения требуется ЦСС со скоростью передачи 128-256 Кбит/с. Трафик мультимедиа включает в себя практически все основные виды трафика за исключением передачи данных. Требования по пропускной способности к ЦСС определяются при планировании и проектировании конкретных систем в зависимости от видов трафика мультимедиа Трафик передачи данных корпоративной ЦСС характеризуется значительной неоднородностью, взрывообразным характером во времени и требует для своей передачи в разные моменты времени разной полосы пропускания. Реальный объем передаваемых по сети данных складывается непосредственно из данных (полезной нагрузки) и необходимого информационного обрамления, составляющего накладные расходы на передачу. Многие технологии устанавливают ограничения на минимальный и максимальный размеры пакета. Например, для технологии Х.25 максимальный размер пакета составляет 4096 байт, а в технологии Frame Relay максимальный размер кадра составляет 8096 байт. Трафик характеризуется следующими основными показателями: – показателем взрывообразного характера трафика; – терпимостью к задержкам; – временем ответа; – емкостью и пропускной способностью. Показатель взрывообразного характера (взрывообразности) трафика определяет частоту посылки данных пользователем в сеть. Этот показатель определяется отношением максимального (пикового) значения плотности трафика (скорости передачи) к ее среднему значению. Терпимость к задержкам характеризует реакцию приложений на все временные задержки в сети. Для приложений, работающих в реальном масштабе времени (например, для видеоконференций), время задержки не должно превышать некоторого предельного значения, которое достаточно мало. Для других приложений допустимые значения задержки могут составлять от нескольких минут до нескольких часов (например, электронная почта и пересылка файлов). Емкость – это реальное количество ресурсов, доступных пользователю на определенном пути передачи данных. Пропускная способность определяется общим количеством данных, которые могут быть переданы в единицу времени. Емкость сети отличается от пропускной способности сети из-за наличия накладных расходов, которые зависят от способа использования сети. 1.2 Общий анализ трафика Для каждой категории трафика в ЦСС устанавливаются соответствующие им приоритеты. Трафик с более высоким приоритетом обрабатывается в первую очередь. При этом приоритеты используются для выделения групп, прикладных программ и отдельных пользователей в группах. Введение приоритетов также неизбежно при недостаточности ресурсов сети. Результаты исследований показывают, что при передаче низкокачественной аудиоинформации с места пожара и ликвидации чрезвычайных ситуаций по сети максимальная задержка сигнала не должна превышать значений 100 – 150 мс, а при передаче изображений – не более 30 мс. Передача голосовых сообщений без искажений возможна при задержке не более 50 мс. В установившемся режиме N-канального бесприоритетного обслуживания простейших потоков с отказами вероятность события занятости k каналов 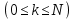 или вероятность отказа Pот в обслуживании (это вероятность занятости PN всех N каналов) определяется формулой Эрланга (1): или вероятность отказа Pот в обслуживании (это вероятность занятости PN всех N каналов) определяется формулой Эрланга (1):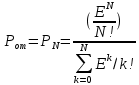 , (1) , (1)где E – относительное значение времени обслуживания одним каналом или плотность потока событий (плотность трафика в эрлангах). Физический смысл интенсивности или плотности Е потока событий (трафика) – это среднее число событий, приходящееся на единицу времени для данного момента. Плотность потока событий или трафика может быть любой неотрицательной функцией времени и имеет размерность 1/с. Применительно к ЦСС плотность трафика нормируется на 1 ч. Поэтому 1 Эрланг – это относительное время занятости канала за 1 ч. Формула Эрланга остается основополагающей для анализа трафика и в ЦСС. Основой маршрутизации трафика в ЦСС является принцип распределения большого числа каналов (входов) от абонентов сети между меньшим числом выходов на коммутационных узлах в ЦСС. При этом требование на предоставление абоненту выхода в сеть возникает и снимается случайным образом. Требование на обслуживание количественно выражается плотностью трафика в Эрлангах Е, т.е. суммой средних требований на обслуживание всех входов одним каналом за единицу времени (или относительное значение среднего времени обслуживания одним каналом) в 1 час определяется следующей формулой: 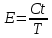 , (2) , (2)где С – число вызовов за время Т, t – средняя длительность вызовов. Для оценки качества обработки трафика используется плотность трафика E, соответствующая периоду максимальной нагрузки или периоду пиковой нагрузки на один канал. Целью оптимального проектирования ЦСС является обеспечение для заданного числа выходов N максимально возможного значения удельной плотности трафика Е или отношения E/N. Допустимое значение E/N должно соответствовать приемлемому значению показателя качества обработки трафика, за которое принята вероятность занятия всех выходов одновременно, т.е. вероятность события, приводящего к потере вызова. Таким образом, вероятность потери одного вызова PN в ЦСС с N выходами в периоды пиковой нагрузки определяет значение показателя качества обработки трафика PN. Чем больше N, тем меньше PN, но тем выше качество обработки трафика, так как общая нагрузка распределяется между большим числом выходов (каналов). Зависимость вероятности потери вызова PN от плотности потока заявок на обслуживание (плотности потока трафика) E и числа выходов N в ЦСС определяется формулой Эрланга, используя которую можно построить графические зависимости отношения E/N от PN при разных значениях N, которые представлены на следующем рисунке (рисунок 1): 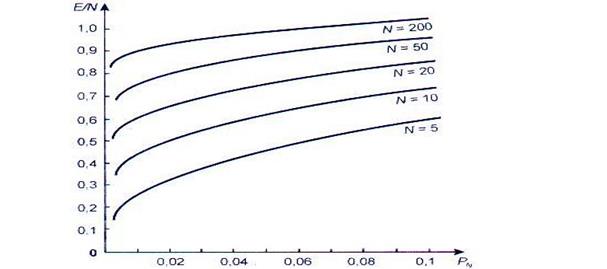 Рисунок 1 – Зависимости удельной плотности трафика, переносимого одним каналом (выходом), от вероятности потери одного вызова Удельная плотность трафика E/N или нормированный закон Эрланга часто используется в качестве основного параметра для расчета и оптимизации трафика в сети связи. На основе оценки пропускной способности магистральных сетей и анализа трафика в создаваемой или развиваемой ЦСС можно планировать ее реальную загрузку. Это позволяет делать определенные выводы в пользу выбора той сетевой технологии и архитектуры, которые в наибольшей степени соответствуют требованиям, предъявляемым к планируемой сети с учетом конкретных условий и решаемых задач. 2 Разновидности моделей сети2.1 Модели ЭрлангаНа настоящий момент существует несколько видов моделей Эрланга: модель Эрланга А, модель Эрланга В и модель Эрланга С. Модель Эрланга А – система с ограничением времени ожидания и времени обслуживания, т.е. система с очередностью обслуживания. Вызовы при занятых каналах становятся в очередь и ждут освобождения канала ограниченное время. Данная модель используется при проектировании сотовых сетей. Модель Эрланга В – система с отказами. Вызовы при занятых каналах связи аннулируются. Данная модель используется при проектировании сотовых сетей связи. Модель Эрланга С – система с ожиданиями. Вызовы при занятых каналах становятся в очередь и ждут освобождения канала неопределенно долгое время. Данная модель используется при проектировании транкинговых сетей связи. Все указанные модели подчиняются следующим дополнительным условиям: – количество абонентов бесконечно велико; – интервалы между вызовами случайны; – длительность вызовов случайна; – время установления соединения ничтожно мало; – вызов, поступивший первым в очередь, первым же ее и покидает; – ресурсы предоставляются в соответствии с порядком поступления запроса. Модель Эрланга А – это система с очередностью обслуживания. В системе, описываемой моделью Эрланга А вызов, поступивший в момент занятости всех каналов, становится в очередь, но при этом время ожидания не превышает среднего времени обслуживания. Если в течении этого времени хотя бы один канал СПД освобождается, находящийся первым в очереди вызов его занимает. С учетом указанной детализации, вероятность отказа в данной системе согласно общей формуле Эрланга выглядит следующим образом: 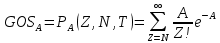 , (8) , (8)где 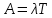 – средний трафик системы (Эрл.). – средний трафик системы (Эрл.).Модель Эрланга В – это система с отказами. Система с отказами является наиболее распространенным типом АССиПД. Для систем такого рода формула Эрланга для определения вероятности отказа в обслуживании выглядит следующим образом: 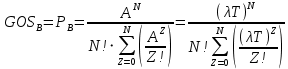 . (9) . (9)Вероятность того, что вызов будет блокирован рассчитывается по следующей формуле: 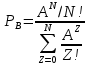 . (10) . (10)Вероятность того, что все каналы будут свободны рассчитываются по следующей формуле: 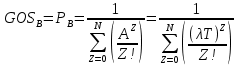 . (11) . (11)Вероятность того, что занято будет K каналов рассчитывается по следующей формуле: 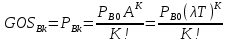 . (12) . (12)Среднее число занятых каналов рассчитывается по следующей формуле: 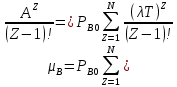 . (13) . (13)Модель Эрланга С – это система с ожиданиями. Для системы с ожиданиями, формула Эрланга определяет вероятность задержки обслуживания, т.е. вероятность постановки в очередь, которая рассчитывается по следующей формуле: 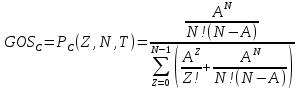 . (14) . (14)Вероятность того, что вызов будет удержан (поставлен в очередь) рассчитывается по следующей формуле: 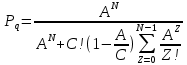 . (15) . (15)Вероятность того, что все каналы будут свободны, рассчитывается по следующей формуле: 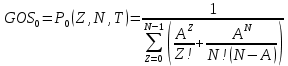 . (16) . (16)Вероятность того, что занято будет K каналов, рассчитывается следующим образом: 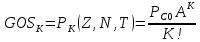 . (17) . (17)Среднее число занятых каналов рассчитывается по следующей формуле: 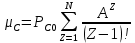 . (18) . (18)Рассмотренные аналитические выражения являются неудобными, поэтому на практике используют табулированные значения данных формул. Рассмотрим пример данных табулированных значений (рисунок 5). 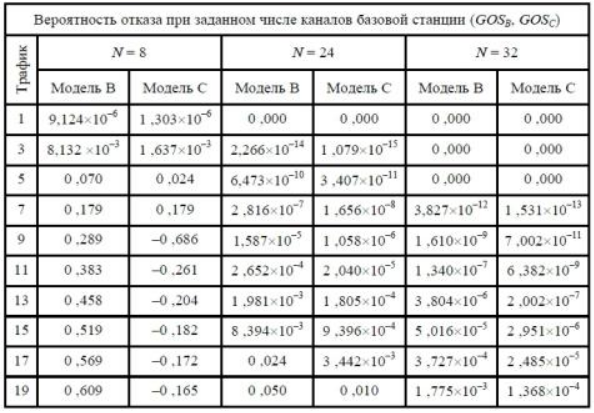 Рисунок 5 – Табулированные значения для моделей Эрланга В и С 2.2 Модели ПолачекаЗаявки разных типов (приоритетов) образуют как бы несколько очередей, по одной очереди на каждое значение приоритета, и в каждый момент, когда сервер заканчивает обслуживание какой-то заявки, на обслуживание направляется заявка из первой в порядке убывания приоритета непустой очереди. Приоритет заявки может быть: – статическим (не меняющимся с течением времени пребывания в системе); – динамическим (может, например, увеличиваться с длительностью ожидания заявки). Для времени ожидания заявки в очереди справедлива формула Полачека: 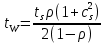 , (19) , (19)где 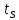 – среднее время обслуживания заявки; – среднее время обслуживания заявки; 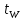 – среднее время ожидания заявки в очереди; – среднее время ожидания заявки в очереди; 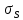 – среднеквадратическое (стандартное) отклонение времени обслуживания прибора; – среднеквадратическое (стандартное) отклонение времени обслуживания прибора; 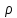 – коэффициент использования прибора – коэффициент использования прибора 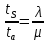 ; ; 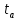 – средний интервал времени между поступлением заявок; – средний интервал времени между поступлением заявок; 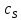 – коэффициент вариации времени обслуживания – коэффициент вариации времени обслуживания 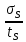 . .Число заявок, ожидающих обслуживания (среднюю длина очереди), можно найти, умножив 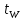 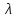 : :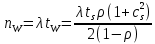 . (20) . (20)Опираясь на следующее равенство: 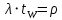 . (21) . (21)Получаем следующее выражение: 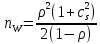 . (22) . (22)Формула Полачека используется для оценивания длин очередей при проектировании информационных систем. Она применяется в случае экспоненциального распределения времени поступления при любом распределении времени обслуживания и любой дисциплине управления, лишь бы выбор очередного сообщения для обслуживания не зависел от времени обслуживания. При проектировании систем встречаются такие ситуации возникновения очередей, когда дисциплина обслуживания выбирается в зависимости от времени обслуживания. Например, в некоторых случаях для первоочередного обслуживания могут выбираться более короткие сообщения с тем, чтобы получить меньшее среднее время обслуживания (среднее время пребывания в заявки системе). При управлении линией связи (каналом Интернет) можно присвоить входным сообщениям более высокий приоритет, чем выходным, поскольку первые короче. В таких случаях уже необходимо использовать не уравнение Полачека или производные от него, а более сложные уравнения или использовать метод имитационного моделирования. Особый интерес для практических применений представляют два случая: – время обслуживания постоянно; – время обслуживания имеет экспоненциальное распределение. При регулярном характере потока рассеяние отсутствует, поэтому среднеквадратическое отклонение 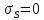 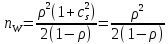 , (23) , (23)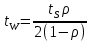 . (24) . (24)И другой случай, когда время обслуживания имеет экспоненциальное распределение. В случае экспоненциального распределения, как известно, среднеквадратическое отклонение  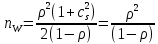 , (25) , (25)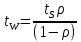 . (26) . (26)Большинство значений времени обслуживания в информационных системах лежит где-то между этими двумя случаями. Времена обслуживания, равные постоянной величине, встречаются редко. Даже время доступа к твердому диску непостоянно из-за различного положения массивов с данными на поверхности. Одним из примеров, иллюстрирующих случай постоянного времени обслуживания может служить занятие линии связи для передачи сообщений фиксированной длины. С другой стороны, разброс времени обслуживания обычно не так велик, как в случае произвольного или экспоненциального его распределения, т.е., 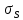 редко достигает значений редко достигает значений 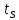 . Этот случай иногда считают наихудшим и потому пользуются формулами, относящимися к экспоненциальному распределению времен обслуживания. Такой расчет может дать несколько завышенные размеры очередей и времен ожидания в них, но эта ошибка, по крайней мере, не опасна. . Этот случай иногда считают наихудшим и потому пользуются формулами, относящимися к экспоненциальному распределению времен обслуживания. Такой расчет может дать несколько завышенные размеры очередей и времен ожидания в них, но эта ошибка, по крайней мере, не опасна.Экспоненциальное распределение времен обслуживания не наихудший случай, с которым приходится иметь дело в действительности. Однако, если времена обслуживания, полученные при расчете очередей, оказываются распределенными хуже, чем времена с экспоненциальным распределением, то это является предостерегающим сигналом для разработчика. Если стандартное отклонение больше среднего значения, то обычно возникает необходимость в коррекции расчетов. 3 Базовые сетевые топологииВ настоящее время термин «топология» является важным при организации и построении сетей любого вида: компьютерных, телефонных, мобильных, сетей радио и ТВ-вещания. Термин «топология» (сетевая топология) имеет следующее значение – это конфигурация графа, вершинам которого соответствуют конечные узлы сети (компьютеры) и коммуникационное оборудование (маршрутизаторы), а ребрам – физические или информационные связи между вершинами. На сегодняшний день нужно выбрать такую топологию, которая обеспечила бы надежную и эффективную работу сети, удобное управление потоками сетевых данных. Желательно также, чтобы сеть по стоимости создания и сопровождения получилась недорогой, но в то же время оставались возможности для ее дальнейшего расширения и, желательно, для перехода к более высокоскоростным технологиям связи. Все соединения с сетью осуществляются посредством специальных сетевых кабелей. Основными характеристиками сетевого кабеля являются скорость передачи данных и максимально допустимая длина. Обе характеристики определяются физическими свойствами кабеля. В качестве сетевого кабеля могут применяться и телефонные линии. Существует несколько типов сетевого кабеля. Разберем каждый из них более детально. Витая пара – позволяет передавать информацию со скоростью 10 Мбит/с (либо 100 Мбит/с), легко наращивается. Длина кабеля не может превышать 1000 м при скорости передачи 10 Мбит/с. Иногда используют экранированную витую пару, т. е. витую пару, помещенную в экранирующую оболочку. Толстый Ethernet кабель – коаксиальный кабель с волновым сопротивлением 50 Ом. Обладает высокой помехозащищенностью. Максимально доступное расстояние без повторителя не превышает 500 м, а общее расстояние сети Ethernet – около 3000 м. Тонкий Ethernet кабель – это также 50-омный коаксиальный кабель со скоростью передачи информации в 10 Мбит/с. Соединения с сетевыми платами производятся при помощи специальных разъемов и тройниковых соединений. Расстояние между двумя рабочими станциями без повторителей может составлять максимум 185 м, а общее расстояние по сети – 1000 м. Оптоволоконные линии – наиболее дорогой тип кабеля. Скорость передачи по ним информации достигает нескольких гигабит в секунду. Допустимое удаление более 50 км. Внешнее воздействие помех практически отсутствует. 3.1 Топология «шина» (bus) В этой топологии все компьютеры соединяются друг с другом одним кабелем (рисунок 6). Посланные в такую сеть данные передаются всем компьютерам, но обрабатывает их только тот компьютер, аппаратный МАС-адрес сетевого адаптера которого записан в кадре как адрес получателя. 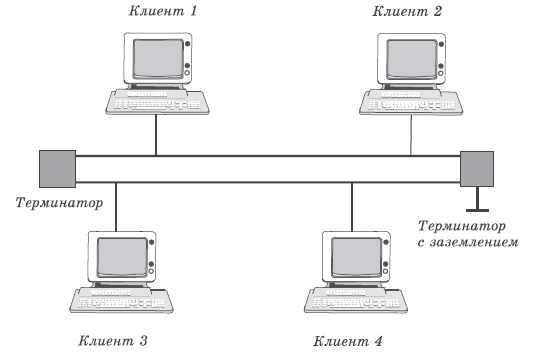 Рисунок 6 – Сеть с топологией «шина» Эта топология исключительно проста в реализации и дешева (требует меньше всего кабеля), однако имеет ряд существенных недостатков. Недостатки сетей типа «шина». Такие сети трудно расширять (увеличивать число компьютеров в сети и количество сегментов – отдельных отрезков кабеля, их соединяющих). Поскольку шина используется совместно, в каждый момент времени передачу может вести толькоодин из компьютеров. Если передачу одновременно начинают два или больше компьютеров, возникает искажение сигнала (столкновение), приводящее к повреждению всех кадров. Тогда компьютеры вынуждены приостанавливать передачу, а затем по очереди ретранслировать данные. Влияние столкновений тем заметнее, чем выше объем передаваемой по сети информации и чем больше компьютеров подключено к шине. Оба этих фактора, естественно, снижают как максимально возможную, так и общую производительность сети, замедляя ее работу. «Шина» является пассивной топологией– компьютеры только «слушают» кабель и не могут восстанавливать затухающие при передаче по сети сигналы. Чтобы удлинить сеть, нужно использовать повторители (репитеры), усиливающие сигнал перед его передачей в следующий сегмент. Надежность сетис топологией «шина»невысока. Когда электрический сигнал достигает конца кабеля, он (если не приняты специальные меры) отражается, нарушая работу всего сегмента сети. Чтобы предотвратить такое отражение сигналов, на концах кабеля устанавливаются специальные резисторы (терминаторы), поглощающие сигналы. Если же в любом месте кабеля возникает обрыв – например, при нарушении целостности кабеля или просто при отсоединении коннектора, – то возникают два незатерминированных сегмента, на концах которых сигналы начинают отражаться, и вся сеть перестает работать. Проблемы, характерные для топологии «шина», привели к тому, что эти сети, столь популярные еще десять лет назад, сейчас уже практически не используются. 3.2 Топология «кольцо» (ring) В данной топологии каждый из компьютеров соединяется с двумя другими так, чтобы от одного он получал информацию, а второму – передавал ее (рисунок 7). Последний компьютер подключается к первому, и кольцо замыкается. 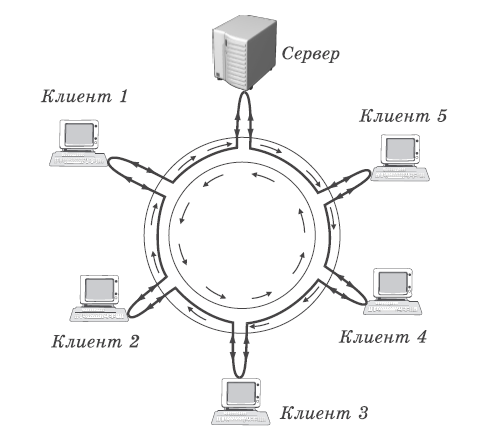 Рисунок 7 – Сеть с топологией «кольцо» Преимущества сетей с топологией «кольцо»: – поскольку у кабелей в этой сети нет свободных концов, терминаторы здесь не нужны; – каждый из компьютеров выступает в роли повторителя, усиливая сигнал, что позволяет строить сети большой протяженности; – из-за отсутствия столкновений топология обладает высокой устойчивостью к перегрузкам, обеспечивая эффективную работу с большими потоками передаваемой по сети информации. Недостатки: – сигнал в «кольце» должен пройти последовательно (и только в одном направлении) через все компьютеры, каждый из которых проверяет, не ему ли адресована информация, поэтому время передачи может быть достаточно большим; – подключение к сети нового компьютера часто требует ее остановки, что нарушает работу всех других компьютеров; – выход из строя хотя бы одного из компьютеров или устройств нарушает работу всей сети; – обрыв или короткое замыкание в любом из кабелей кольца делает работу всей сети невозможной; – чтобы избежать остановки работы сети при отказе компьютеров или обрыве кабеля, обычно прокладывают два кольца, что существенно удорожает сеть. Здесь, так, как и для сетей с топологией «шина», недостатки несколько перевешивают достоинства, в результате чего популярные ранее кольцевые сети теперь используются гораздо реже. 3.3 Топология «звезда» (star) Эта топология возникла на заре вычислительной техники, когда к мощному центральному компьютеру подключались все остальные абоненты сети. В такой конфигурации все потоки данных шли исключительно через центральный компьютер; он же полностью отвечал за управление информационным обменом между всеми участниками сети. Конфликты при такой организации взаимодействия в сети были невозможны, однако нагрузка на центральный компьютер была столь велика, что ничем другим, кроме обслуживания сети, этот компьютер, как правило, не занимался. Выход его из строя приводил к отказу всей сети, тогда как отказ периферийного компьютера или обрыв связи с ним на работе остальной сети не сказывался. Сейчас такие сети встречаются довольно редко. Гораздо более распространенной сегодня топологией является похожий вариант – «звезда-шина» (рисунок 8). Здесь периферийные компьютеры подключаются не к центральному компьютеру, а к пассивному концентратору, или хабу (hub). Последний, в отличие от центрального компьютера, никак не отвечает за управление обменом данными, а выполняет те же функции, что и повторитель, то есть восстанавливает приходящие сигналы и пересылает их всем остальным подключенным к нему компьютерам и устройствам. Именно поэтому данная топология, хотя физически и выглядит как «звезда», логически является топологией «шина». 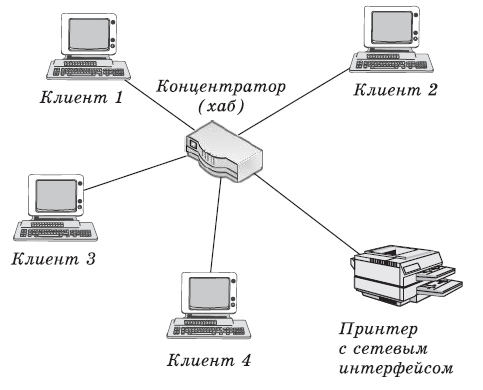 Рисунок 8 – Сеть с топологией «звезда-шина» Несмотря на больший расход кабеля, характерный для сетей типа «звезда», эта топология имеет существенные преимущества перед остальными, что и обусловило ее широчайшее применение в современных сетях. Преимущества сетей типа «звезда-шина»: а) надежность – подключение к центральному концентратору и отключение компьютеров от него никак не отражается на работе остальной сети; обрывы кабеля влияют только на единичные компьютеры; б) легкость при обслуживании и устранении проблем – все компьютеры и сетевые устройства подключаются к центральному соединительному устройству, что существенно упрощает обслуживание и ремонт сети; в) защищенность – концентрация точек подключения в одном месте позволяет легко ограничить доступ к жизненно важным объектам сети. Таким образом, можно сделать вывод, что топология «звезда-шина» является наиболее подходящей для организации сети, поскольку имеет наименьшее количество недостатков и наибольшее количество преимуществ. 3.4 Новые типовые топологические решенияРеальные компьютерные сети постоянно расширяются и модернизируются. Поэтому почти всегда такая сеть является гибридной, т. е. ее топология представляет собой комбинацию нескольких базовых топологий. Легко представить себе гибридные топологии, являющиеся комбинацией «звезды» и «шины», либо «кольца» и «звезды». Однако особо следует выделить топологию «дерево» (tree), которую можно рассматривать как объединение нескольких «звезд» (рисунок 9). Именно эта топология сегодня является наиболее популярной при построении локальных сетей.  Рисунок 9 – Сеть с топологией «дерево» Таким образом, можно сделать вывод, что сеть с данной топологией легко увеличить и легко её контролировать (поиск обрывов и неисправностей), поскольку данная сеть собрала в себе свойства других топологий. 3.5 Типовые топологии транспортной сети Транспортная сеть (transport network) – часть сети связи, охватывающая магистральные узлы, междугородние станции, а также соединяющие их каналы и узлы (национальные, междугородные). Первичные сети, являющиеся базовыми транспортными или магистральными сетями, служат основой для построения всего многообразия современных мультисервисных сетей связи. Таким образом, первичной сетью называется совокупность типовых физических цепей, типовых каналов передачи и сетевых трактов системы электросвязи, образованная на базе сетевых узлов, сетевых станций, оконечных устройств первичной сети и соединяющих их линий передачи системы электросвязи. Главным требованием, предъявляемым к транспортным сетям, является выполнение сетью основной функции – обеспечения пользователям возможности доступа ко всем разделяемым ресурсам сети. При построении топологии планируемой транспортной сети необходимо предусматривать необходимое резервирование сетевых элементов на аппаратном и сетевом уровне, резервирование трафика, увязать топологию сети с организацией ее управления и синхронизации, предусмотреть организацию соответствующих сетей доступа и их подключение к ЦПС. Топология "точка–точка". Сегмент сети, связывающий два узла A и B, или топология "точка–точка", является наиболее простым примером базовой топологии SDH сети (рисунок 10). Она может быть реализована с помощью терминальных мультиплексоров ТМ, как по схеме без резервирования канала приёма/передачи, так и по схеме со стопроцентным резервированием типа 1+1, использующей основной и резервный электрические или оптические агрегатные выходы (каналы приёма/передачи). 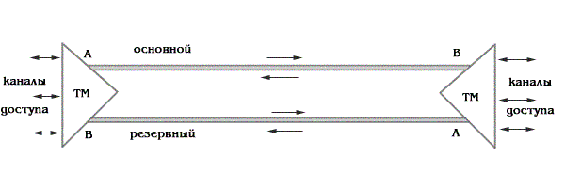 Рисунок 10 – Топология "точка-точка", реализованная с использованием ТМ Топология "последовательная линейная цепь". Эта базовая топология используется тогда, когда интенсивность трафика в сети не так велика и существует необходимость ответвлений в ряде точек линии, где могут вводиться каналы доступа. Она может быть представлена либо в виде простой последовательной линейной цепи без резервирования, как на рисунке 11, либо более сложной цепью с резервированием типа 1+1, как на рисунке 12. Последний вариант топологии часто называют "упрощённым кольцом". 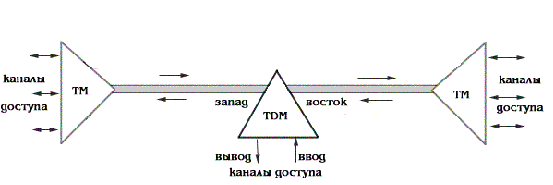 Рисунок 11 – Топология "последовательная линейная цепь", реализованная на ТМ и TDM. 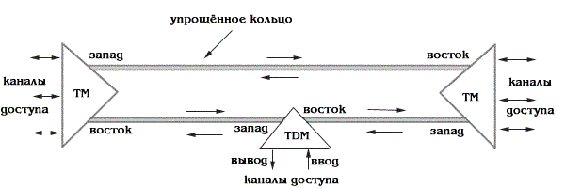 Рисунок 12 – Топология "последовательная линейная цепь" типа "упрощённое кольцо" с защитой 1+1. Топология "кольцо". Эта топология (рисунок 13) широко используется для построения SDH сетей первых двух уровней SDH иерархии (155 и 622 Мбит/с). Основное преимущество этой топологии – лёгкость организации защиты типа 1+1, благодаря наличию в синхронных мультиплексорах SMUX двух пар оптических каналов приёма/передачи: восток – запад, дающих возможность формирования двойного кольца со встречными потоками. 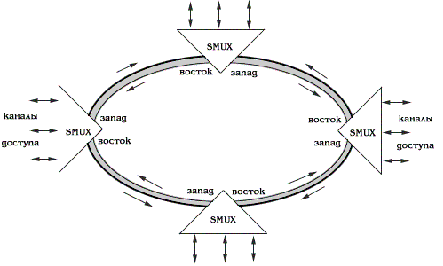 Рисунок 13 – Топология "кольцо" c защитой 1+1 |
