Список задач по данной теме. Обработка данных, вводимых из файла в виде последовательности чисел

• Название: Обработка данных, вводимых из файла в виде последовательности чисел
• Анкор: Список задач по данной теме
• Дата: 14.01.2022
• Размер: 423 Kb.
• Имя файла: ege27.doc
• Тип: Документы; #330752
• страница: 1 из 7

© К. Поляков, 2009-2021

27 (высокий уровень, время – 35 мин)

Тема: Обработка данных, вводимых из файла в виде последовательности чисел.

Что проверяется:

Умение создавать собственные программы (20–40 строк) для анализа числовых последовательностей.

1.6.3. Построение алгоритмов и практические вычисления.

1.1.3. Строить информационные модели объектов, систем и процессов в виде алгоритмов.

Что нужно знать:

• 
  как прочитать данные из файла
  
• 
  основы комбинаторики
  
• 
  динамическое программирование
  

Благодаря тому, что в компьютерном ЕГЭ само решение не проверяется и основной задачей становится получение правильного ответа, скорее всего не будет задач 27, которые можно решить переборными алгоритмами с квадратичной сложностью (оценка O(n²)). Задача 27 в демо-варианте КИМ даёт представление и типе задач, которые такими алгоритмами не решаются. Вероятно, будут предложены задачи, в которых полный перебор вариантов имеет сложность O(2^N) или O(N!), однако использование динамического программирования позволяет быстро решить задачу за один проход.

Материалы от Alex Danov:

• 
  Базовые алгоритмы для решения задач ЕГЭ на программирование: https://www.youtube.com/playlist?list=PLXZ932--vmI_-BWxVtEdU-p-_BtnYfR8p
  
• 
  Решения задач из сборника 2020 г.: https://github.com/AlexDanov/InfEGE-27-PascalABC
  
• 
  Разборы задач 27 (из сборника 2020 г.): https://www.youtube.com/playlist?list=PLXZ932--vmI_ivq9QOC_gpZ2czSe2CLTU
  

Пример задания:

Р-03. (демо-2022) Дана последовательность из N натуральных чисел. Рассматриваются все её непрерывные подпоследовательности, такие что сумма элементов каждой из них кратна k = 43. Найдите среди них подпоследовательность с максимальной суммой, определите её длину. Если таких подпоследовательностей найдено несколько, в ответе укажите количество элементов самой короткой из них.

Входные данные

Даны два входных файла (файл A и файл B), каждый из которых содержит в первой строке количество пар N (1 ≤ N ≤ 10⁸). Каждая из следующих N строк содержит одно натуральное число, не превышающих 10000.

Пример организации исходных данных во входном файле:

7

21

13

9

19

17

26

95

В этом наборе можно выбрать последовательности 21+13+9 (сумма 43) и 17+26 (сумма 43). Самая короткая из них, 17 + 26, имеет длину 2. Для указанных программа должна вывести число 2.
В ответе укажите два числа: сначала значение искомой суммы для файла А, затем для файла B.

Решение:

1. 
   Применим метод динамического программирования, при котором решение будет изменяться при получении очередного числа из файла. Это позволит решить задачу за один проход (сложность будет линейная, O(N)). Решение для любого из заданных файлов будет найдено не более за несколько секунд на любом языке программирования.
   
2. 
   Напишем решение сначала на языке Python. Откроем файл и прочитаем количество чисел из первой строки:
   

F = open("27.txt")

N = int( F.readline() )

3. 
   Будем накапливать сумму всех прочитанных чисел в переменной totalSym: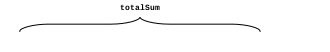
   

Серым цветом обозначены элементы последовательности, которые уже прочитаны из файла. В программе это выглядит так:

K = 43

totalSum = 0

for i in range(1,N+1):

x = int( F.readline() )

totalSum += x

r = totalSum % K

В переменной r вычисляется остаток от деления полученной суммы на K.

4. 
   Предположим, что нужная нам последовательность заканчивается как раз на последнем значении x, прочитанном из файла. Для того чтобы сумма элементов этой последовательности делилась на K, нужно «убрать» из неё первые несколько значений, сумма которых tailSum при делении на K даёт в остатке r, так же, как и totalSum.
   

Поскольку обе суммы дают одинаковый остаток при делении на K, их разность будет делиться на K без остатка. Так как нам нужная наибольшая сумма totalSum-tailSum и все числа в последовательности положительные, нужно использовать минимально возможное значение tailSum (если такая сумма с остатком r есть).

5. 
   Таким образом, при просмотре последовательности нужно определять tailSum для каждого остатка r (от 0 до K-1). Для этой цели будем использовать массив, который инициализируется так:
   

tailSum = [0] + [None]*(K-1)

В самом начале известно только одно (нулевое) значение tailSum для остатка 0. Остальные неизвестны, и поэтому в массив мы добавляем K-1 значение, равное None.

6. 
   Для того чтобы определить длину выбранной последовательности нам нужно знать, сколько элементов входят в «хвостовую» последовательности с суммой tailSum[r]. Для этого используется еще один массив размера K:
   

tailLen = [0]*K

Значение tailLen[r] – это длина «хвоста», сумма элементов которого при делении на K дает остаток r.

Итак, мы читаем очередное значение x их файла и добавляем его к сумме totalSum. Далее возможно два варианта:

а) значение tailSum[r] существует (не равно None), значит, мы нашли очередную последовательность с суммой, кратной K; сумма этой последовательности равна totalSum-tailSum[r], а её длина равна i-tailLen[r], где i – это порядковый номер прочитанного значения (отсчёт ведётся с единицы), так что i равно общему количеству элементов последовательности, прочитанных из файла на данный момент.

б) значение tailSum[r] НЕ существует (равно None), значит, мы не можем построить подходящую последовательность; в этом случае в totalSum мы как раз и получили значение tailSum[r], которое пригодится нам далее.

Нам нужно искать подходящую последовательность с максимальной суммой и минимальной длиной, для хранения этих данных введём переменные maxSum и minLen:

maxSum, minLen = 0, 0

7. 
   Однопроходный алгоритм решения этой задачи, основанный на описанной выше идее, выглядит так:
   

for i in range(1,N+1):

x = int( F.readline() )

totalSum += x

r = totalSum % K

if tailSum[r] != None:

# нашли новую последовательность

curSum = totalSum - tailSum[r]

curLen = i - tailLen[r]

# если сумма больше или при той же сумме длина

# меньше, запоминаем новые сумму и длину

if curSum > maxSum or \

(curSum == maxSum and curLen < minLen):

maxSum = curSum

minLen = curLen

else:

# запоминаем данные «хвоста» для дальнейшего

tailSum[r] = totalSum

tailLen[r] = i

После этого остается только закрыть файл и вывести значение minLen.

8. 
   Приведём полное решение задачи на Python:
   

F = open("27.txt")

N = int( F.readline() )

K = 43

tailSum = [0] + [None]*(K-1)

tailLen = [0]*K

maxSum, minLen = 0, 0

totalSum = 0

for i in range(1,N+1):

x = int( F.readline() )

totalSum += x

r = totalSum % K

if tailSum[r] != None:

curSum = totalSum - tailSum[r]

curLen = i - tailLen[r]

if curSum > maxSum or \

(curSum == maxSum and curLen < minLen):

maxSum = curSum

minLen = curLen

else:

tailSum[r] = totalSum

tailLen[r] = i

F.close()

print( minLen )

9. 
   Аналогичное решение на PascalABC.NET:
   

##

Assign(input, '27-75b.txt');

var N := ReadINteger;

var K := 43;

var tailSum := |0| + |-1|*(K-1);

var tailLen := |0|*K;

var (maxSum, minLen) := (0, 0);

var totalSum := 0;

for var i:=1 to N do begin

var x := ReadInteger;

totalSum += x;

var r := totalSum mod K;

if tailSum[r] <> -1 then begin

var curSum := totalSum - tailSum[r];

var curLen := i - tailLen[r];

if (curSum > maxSum) or

((curSum = maxSum) and (curLen < minLen)) then begin

maxSum := curSum;

minLen := curLen;

end

end else begin

tailSum[r] := totalSum;

tailLen[r] := i;

end

end;

print( minLen );

10. 
    Аналогичное решение на C++:
    

#include

#include

using namespace std;
int main()

{

const int K = 43;

ifstream F("27-75a.txt");

int N;

F >> N;

int tailSum[K] = {0};

for( int i=1;i

int tailLen[K] = {0};

int maxSum = 0;

int minLen = 0;

int totalSum = 0;

for( int i=1; i<=N; i++ ) {

int x;

F >> x;

totalSum += x;

int r = totalSum % K;

if( tailSum[r] != -1 ) {

int curSum = totalSum - tailSum[r];

int curLen = i - tailLen[r];

if( (curSum > maxSum) or

((curSum == maxSum) and (curLen < minLen)) ) {

maxSum = curSum;

minLen = curLen;

}

}

else {

tailSum[r] = totalSum;

tailLen[r] = i;

}

}

cout << minLen;

}

Ещё пример задания:

Р-02. (А. Кабанов) В файле записана последовательность натуральных чисел. Гарантируется, что все числа различны. Рассматриваются всевозможные непустые подмножества, состоящие из элементов последовательности. Необходимо найти количество подмножеств, в которых сумма элементов кратна 12.

Входные данные

Даны два входных файла (файл A и файл B), каждый из которых содержит в первой строке количество пар N (1 ≤ N ≤ 100000). Каждая из следующих N строк содержит одно натуральное число, не превышающих 10⁶.

Пример организации исходных данных во входном файле:

4

5

7

12

23

Для указанных данных можно выбрать следующие подмножества: {12}; {5, 7}; {5, 7, 12}. Программа должна вывести количество этих множеств – 3. В ответе укажите два числа: сначала значение искомой суммы для файла А, затем для файла B.

Решение (А. Кабанов):

11. 
    Рассмотрим динамическое решение, при котором очередное прочитанное из файла число будет добавляться к уже найденным подмножествам. Полученные подмножества будут добавлять к уже существующим для подсчёта на следующих шагах. Все подмножества классифицируем на 12 групп: по остаткам от деления суммы элементов на 12.
    
12. 
    Для начала откроем файл, прочтём количество чисел и создадим массив k, в котором будем считать количество подмножеств с остатками от деления сумм элементов 0, 1, ..., 11.
    

f = open('27.txt')

n = int(f.readline())

k = [0]*12

13. 
    При чтении нового числа x создаём копию массива в переменной k1 для добавления новых подмножеств.
    

for i in range(n):

x = int(f.readline())

k1 = k.copy()

14. 
    Добавление каждого нового числа удваивает количество подмножеств предыдущих элементов. При этом суммы новых подмножеств увеличатся ровно на значение нового числа и соответствующим образом поменяют свой остаток. Таким образом, все предыдущие подмножества с остатком i после добавления числа x изменят свой остаток на (i + x) % 12. Эти подмножества добавляются к уже посчитанным с тем же остатком:
    

for i in range(n):

x = int(f.readline())

k1 = k.copy()

for i in range(12):

k1[ (i+x) % 12 ] += k[i]

15. 
    Дополнительно рассматриваем комбинацию с пустым подмножеством, которая даст нам просто число x:
    

k1[ x%12 ]+=1

16. 
    Полученные значения количеств множеств сохраняются в массиве k для подсчёта на следующих шагах.
    

k = k1.copy()

17. 
    После перебора всех чисел из итоговых значений выбираем количество множеств с остатком суммы равным 0:
    

print(k[0])

18. 
    Полная программа на Python:
    

f = open('27.txt')

n = int(f.readline())

k = [0]*12

for i in range(n):

x = int(f.readline())

k1 = k.copy()

for i in range(12):

k1[ (i+x) % 12 ] += k[i]

k1[ x%12 ]+=1

k = k1.copy()

f.close()

print(k[0])

Ещё пример задания:

Р-01. Имеется набор данных, состоящий из пар положительных целых чисел.

Необходимо выбрать из каждой пары ровно одно число так, чтобы сумма всех выбранных чисел делилась на 6 и при этом была максимально возможной. Гарантируется, что искомую сумму получить можно. Программа должна напечатать одно число – максимально возможную сумму, соответствующую условиям задачи.

Входные данные

Даны два входных файла (файл A и файл B), каждый из которых содержит в первой строке количество пар N (1 ≤ N ≤ 100000). Каждая из следующих N строк содержит два натуральных числа, не превышающих 10 000.

Пример организации исходных данных во входном файле:

3

7 4

11 9

5 23

Для указанных входных данных значением искомой суммы должно быть число 36 (выбраны числа 4, 9 и 23, их сумма 36 делится на 6). В ответе укажите два числа: сначала значение искомой суммы для файла А, затем для файла B.

Решение:

1. 
   в отличие от задачи Р-00, разобранной ниже, здесь требование обратное: нужно, чтобы набранная сумма ДЕЛИЛАСЬ на заданное число, и это значительно осложняет дело;
   
2. 
   общая структура программы, которая читает данные из файла, подробно рассмотрена ниже при разборе задачи Р0-00:
   

Fin = open( "27.txt" )

N = int( Fin.readline() )

for i in range(N):

a, b = map( int, Fin.readline().split() )

... # обработка данных

Fin.close()

# вывод результата

3. 
   представим себе идеальную ситуацию: мы нашли сумму самых больших чисел в паре, и она делится на 6 (ура!), тогда остается её вывести на экран:
   

D = 6

s = 0

for i in range(N):

a, b = map( int, Fin.readline().split() )

s += max( a, b )

if s % D == 0:

print( s )

здесь для общности решения число, на которое должна делиться сумма, записано в переменную D (в других языках это должна быть константа)

4. 
   а вот если полученная сумма не делится на 6, нам придётся заменить числа в одной или нескольких парах так, чтобы «убрать» остаток от деления на 6, то есть вычесть из суммы всех наибольших чисел значение, которое имеет тот же остаток от деления на 6, что и сумма s
   
5. 
   отсюда следует, что для каждого возможного остатка от 1 до 5 нам нужно хранить в памяти наименьшие значения, которые можно вычесть из суммы; для этого нужен массив dMin
   
6. 
   если нам повезёт, такая коррекция выполняется заменой всего в одной паре; тогда можно сделать так:
   

а) сначала во все элементы массива dMin записываем число, которое заведомо больше, чем все числа в файле, например, 10001

б) прочитав очередную пару чисел, определяем r – остаток от деления разности чисел в паре (по модулю) на 6

в) сравниваем модуль разности abs(a-b) со значением dMin[r], наименьшее из них сохраняем в элементе массива dMin[r]:

D = 6

dMin = [10001] * D

s = 0

for i in range(N):

a, b = map( int, Fin.readline().split() )

s += max( a, b )

d = abs( b – a )

r = d % D

if r > 0:

dMin[r] = min( d, dMin[r] )

if s % D == 0:

print( s )

else:

print( s – dMin[r] )

7. 
   однако, запустив нашу программу на тестовых исходных данных, приведённых в описании задачи, получаем ответ: –9960.
   
8. 
   это означает, что одной заменой не обойтись (иногда можно обойтись и одной заменой, но полученная сумма вполне может оказаться меньше наибольшей, которую можно получить только с помощью нескольких замен).
   
9. 
   итак, в текущей паре мы получили разность d с остатком от деления на D, равным r; пусть теперь у нас есть одна из предыдущих пар с остатком k и разностью d1; тогда, сделав замены в двух этих парах, мы уберём остаток (r+k), точнее, с учётом того, что эта сумма может стать больше D, убирается остаток r0=(r+k)%D
   
10. 
    при этом алгоритм изменения массива dMin приобретает вид:
    

if r > 0:

for k in range(1, D):

r0 = (r + k) % D

dMin[r0] = min( d + dMin[k], dMin[r0] )

dMin[r] = min( d, dMin[r] )

11. 
    но здесь таится ещё одна ловушка: на каждой итерации цикла for в предыдущем фрагменте массив dMin изменяется, и велик шанс, что на одном из следующих шагов мы захватим уже изменённый элемент массива, при этом результат будет неверный (получится, что мы дважды сделаем одну и ту же замену);
    
12. 
    поэтому перед изменением массива dMin создадим его копию dMinNew, а затем будем записывать новые значения в эту копию; после завершения всех операций запишем новые элементы в dMin:
    

if r > 0:

dMinNew = dMin[:]

for k in range(1, D):

r0 = (r + k) % D

dMinNew[r0] = min( d+dMin[k], dMinNew[r0] )

dMinNew[r] = min( d, dMinNew[r] )

dMin = dMinNew[:]

13. 
    приведём полную программу на Python:
    

Fin = open("27.txt")

D = 6

N = int( Fin.readline() )
s = 0

dMin = [10001]*D

for i in range(N):

a, b = map( int, Fin.readline().split() )

s += max( a, b )

d = abs( a-b )

r = d % D

if r > 0:

dMinNew = dMin[:]

for k in range(1, D):

r0 = (r + k) % D

dMinNew[r0] = min( d+dMin[k], dMinNew[r0] )

dMinNew[r] = min( d, dMinNew[r] )

dMin = dMinNew[:]

print( a, b, dMin )
Fin.close()
if s % D == 0:

print( s )

else:

print( s - dMin[s % D] )

Решение (программа на PascalABC.NET):

1. 
   Полный текст программы, использующей возможности LINQ (Language-Integrated Query) в PascalABC.NET:
   

const B = 6;

begin

var data := Readlines('27.txt')

.Select(s->s.ToIntegers).ToArray;

var n := data[0].First;

var pairs := data.Skip(1).Take(n);

var sum := pairs.Sum(x->x.Max);

pairs.Aggregate( |0|,

// построить все комбинации сумм

(a,x)-> a.Cartesian(x, (a,b)->a+b)

// сгруппировать по остаткам от деления на 6

.GroupBy(x->x mod B)

// из каждой группы выбрать максимальное

.Select(x->x.Max)

.ToArray)

.Where(x->x.Divs(B))

.Print;

end.

Ещё пример задания:

Р-00(Демо-2021). Имеется набор данных, состоящий из пар положительных целых чисел.

Необходимо выбрать из каждой пары ровно одно число так, чтобы сумма всех выбранных чисел не делилась на 3 и при этом была максимально возможной. Гарантируется, что искомую сумму получить можно. Программа должна напечатать одно число – максимально возможную

сумму, соответствующую условиям задачи.

Входные данные

Даны два входных файла (файл A и файл B), каждый из которых содержит в первой строке количество пар N (1 ≤ N ≤ 100000). Каждая из следующих N строк содержит два натуральных числа, не превышающих 10 000.

Пример организации исходных данных во входном файле:

6

1 3

5 12

6 9

5 4

3 3

1 1

Для указанных входных данных значением искомой суммы должно быть число 32.

В ответе укажите два числа: сначала значение искомой суммы для файла А, затем для файла B.

Решение:

1. 
   вспомним (или научимся), как прочитать данные из файла; сначала нужно открыть файл (сделать активным), затем прочитать данные, и затем его закрыть (освободить);
   
2. 
   в языке Python это выглядит так:
   

Fin = open( "27.txt" )

N = int( Fin.readline() )

for i in range(N):

a, b = map( int, Fin.readline().split() )

... # здесь работаем с переменными a и b

Fin.close()

3. 
   в программе на языке PascalABC.NET достаточно просто переключить поток ввода на файл, и после этого читать из него данные так же, как с клавиатуры:
   

var N, i, a, b: integer;

begin

Assign( input, '27.txt' );

Readln( N );

for i:=1 to N do begin

Readln( a, b );

... // здесь работаем с переменными a и b

end;

...

end.

4. 
   в программе на C++ используем файловые потоки из библиотеки fstream:
   

L = list(map(int, Fin.readline().split()))vbhjy#include

using namespace std;

int main() {

ifstream Fin( "27.txt" );

int N, a, b;

Fin >> N;

for( int i = 0; i < N; i++ ) {

Fin >> a >> b;

... // здесь работаем с переменными a и b

}

...

}

5. 
   пока забудем про требование «чтобы сумма всех выбранных чисел не делилась на 3» и найдём просто максимальную сумму; для этого достаточно выбрать из каждой пары максимальное число:
   

Python:

s = 0

for i in range(N):

a, b = map( int, Fin.readline().split() )

s += max( a, b )

print( s )

PascalABC.NET:

var s := 0;

for i:=1 to N do begin

Readln( a, b );

s += Max(a,b);

end;

Writeln( s )

C++:

int s = 0;

for( int i = 0; i < N; i++ ) {

Fin >> a >> b;

s += max( a, b );

}

cout << s;

6. 
   если полученная сумма не делится на 3, то всё хорошо, а если делится? в этом случае нужно заменить число в одной из пар, вместо максимального взять второе, минимальное;
   
7. 
   при этом для того чтобы сумма получилась максимальной нужно выбрать пару, в которой разница между числами минимальная и не делится на 3 (иначе делимость новой суммы на 3 сохранится)
   
8. 
   будем искать значение dMin – минимальную разницу между числами одной из пар, не делящаяся на 3; тогда при выводе в случае делимости суммы s на 3 выводим s-dMin, что соответствует замене числа в одной паре:
   

Python:

dMin = 10001

for i in range(N):

a, b = map( int, Fin.readline().split() )

s += max( a, b )

d = abs( a-b )

if d % 3 > 0:

dMin = min( d, dMin )

if s % 3 != 0:

print( s )

else:

print( s-dMin )

PascalABC.NET:

var dMin := MaxInt;

for i:=1 to N do begin

Readln( a, b );

s += Max(a,b);

var d := Abs(a-b);

if d mod 3 <> 0 then

dMin := Min( d, dMin )

end;

if s mod 3 <> 0 then

Writeln( s )

else Writeln( s-dMin );

C++:

int dMin = 10001;

for( int i = 0; i < N; i++ ) {

Fin >> a >> b;

s += max( a, b );

int d = abs( a-b );

if( d % 3 > 0 )

dMin = min( d, dMin );

}

if( s % 3 != 0 )

cout << s;

else

cout << s-dMin;

9. 
   приведём полное решение:
   

Python:

Fin = open( "27.txt" )

N = int( Fin.readline() )

s, dMin = 0, 10001

for i in range(N):

a, b = map( int, Fin.readline().split() )

s += max( a, b )

d = abs( a-b )

if d % 3 > 0:

dMin = min( d, dMin )

if s % 3 != 0:

print( s )

else:

print( s-dMin )

PascalABC.NET:

var N, i, a, b : integer;

begin

Assign( input, '27.txt' );

Readln( N );

var s := 0;

var dMin := MaxInt;

for i:=1 to N do begin

Readln( a, b );

s += Max(a,b);

var d := Abs(a-b);

if d mod 3 <> 0 then

dMin := Min(d, dMin)

end;

if s mod 3 <> 0 then

Writeln( s )

else Writeln( s-dMin );

end.

C++:

#include

#include

#include

using namespace std;

int main() {

ifstream Fin( "27-b.txt" );

int N, s = 0, dMin = 10001;

Fin >> N;

for( int i = 0; i < N; i++ ) {

int a, b;

Fin >> a >> b;

s += max( a, b );

int d = abs( a-b );

if( d % 3 > 0 )

dMin = min( d, dMin );

}

if( s % 3 != 0 )

cout << s;

else

cout << s-dMin;

}

10. 
    обработка файла А даёт ответ 127127, а обработка файла B – ответ 399762080
    
11. 
    Ответ: 127127 399762080.
    

Решение (программа, А.М. Кабанов):

1. 
   Основная идея решения в том, чтобы последовательно (при чтении каждой пары) пересчитывать наибольшие суммы с остатками 0, 1, 2. Алгоритм представляет собой вариант динамического программирования.
   
2. 
   Создадим массив m с индексами от 0 до 2, в котором будем хранить наибольшие возможные суммы чисел с остатком 0, 1, 2 соответственно. С каждой новой введённой парой рассматриваются всевозможные суммы чисел из этой пары и максимальных сумм с предыдущего шага. Из этих сумм отбираются наибольшие с остатком 0, 1, 2 и записываются в m для использования в последующих шагах.
   
3. 
   Откроем файл и считаем количество пар чисел в файле
   

assign(input, '27-b.txt');

readln(n);

4. 
   Считываем очередную пару и заполняем временный массив m1 нулями. В m1 мы будем считать максимальные суммы с новой парой.
   

for i:=1 to n-1 do begin

readln(a[0], a[1]);

for j:=0 to 2 do m1[j]:= 0;

...

5. 
   Перебираем всевозможные пары из новых чисел и сумм с предыдущих шагов. Для удобства для каждой суммы вычисляем её остаток от деления на 3. Проверяем, что если этот шаг первый (i = 1) или сумма с предыдущего шага определена (ненулевая) и новая сумма больше старой суммы с тем же остатком, то происходит её замена.
   

for j:=0 to 1 do begin

for k:=0 to 2 do begin

ost:=(a[j]+m[k]) mod 3;

if ((i = 1) or (m[k]<>0)) and (a[j]+m[k]>m1[ost]) then

m1[ost]:=a[j]+m[k];

end;

end;

6. 
   После проверки всех возможных сумм полученный результат в m1 перезаписывает массив m для использования на последующих шагах.
   

...

m:=m1;

end;

7. 
   После анализа всех пар ответом является наибольшая из полученных сумм с ненулевым остатком от деления на 3. Для удобства, воспользуемся функцией max.
   

writeln( max(m[1],m[2]) );

8. 
   Полный код на Pascal:
   

var m, m1: array[0..2] of longint;

var a: array[0..1] of longint;

var ost, i, j, k, n: integer;
begin

assign(input, '27-B.txt');

readln(n);

for i:=1 to n do begin

readln(a[0], a[1]);

for j:=0 to 2 do m1[j]:= 0;

for j:=0 to 1 do begin

for k:=0 to 2 do begin

ost:=(a[j]+m[k]) mod 3;

if ((i = 1) or (m[k]<>0)) and (a[j]+m[k]>m1[ost]) then

m1[ost]:=a[j]+m[k];

end;

end;

m:=m1;

end;

writeln( max(m[1],m[2]) );

end.

9. 
   Полный код аналогичного решения на Python:
   

f = open('27-b.txt')

n = int(f.readline())
m = [0, 0, 0]

for i in range(n):

a = [int(x) for x in f.readline().split()]

m1 = [0, 0, 0]

for x in a:

for y in m:

ost = (x+y)%3

if (i == 0 or y != 0) and x+y > m1[ost]:

m1[ost] = x+y

m = m1.copy()

print( max(m[1], m[2]) )

f.close()

Решение (программа на PascalABC.NET, автор А. Богданов):

2. 
   Полный текст программы, использующей возможности LINQ (Language-Integrated Query) в PascalABC.NET:
   

###

var data := ReadLines('27-a.txt').Skip(1) // выбросили N

.Sel(s->s.ToIntegers).ToA;

var sMax := data.Sum(x->x.Max);

var rMin := data.Sel(x->abs(x[0]-x[1])).Wh(r->r.ND(3)).Min;

Println( sMax.ND(3)? sMax: sMax-rMin );

Решение (электронные таблицы, И.В. Степанов):

1. 
   загружаем текст в Excel с помощью вкладки Данные/Из текста (используем разделитель - пробел); удаляем первую строку где только одно число (количество)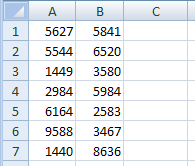
   

2. 
   В столбце C находим максимальное из каждой пары чисел: вставляем в C1 формулу =МАКС(A1:B1) и копируем ее вниз (двойной щелчок на маркере заполнения)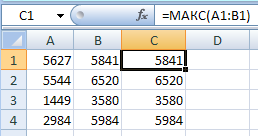
   

3. 
   вычисляем сумму чисел в столбце C: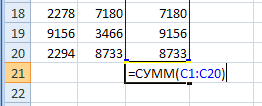
   

4. 
   проверяем кратность 3: находим остаток от деления на 3 по формуле =ОСТАТ(C21;3)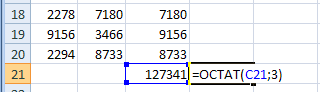
   

5. 
   если остаток не равен 0, то искомое число найдено; иначе продолжаем…
   
6. 
   в столбце D для каждой пары находим модуль разности по формуле вида =ABS(A1-B1);
   
7. 
   поскольку нам нужны только пары, в которых разность не делится на 3, в столбце E для каждой пары находим остатки от деления полученной разности на 3 по формулам вида =ОСТАТ(D1;3).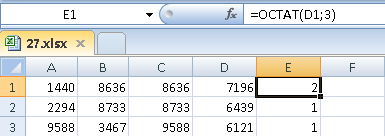
   
8. 
   
   

9. 
   сортируем диапазон по столбцу D по убыванию (возрастанию) и берем минимальное значение (минимальную разницу в паре) с ненулевым остатком в соседней ячейке столбца E.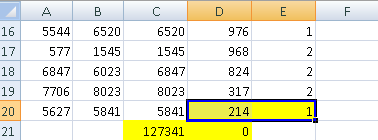
   

10. 
    вычитаем его из суммы, полученной ранее: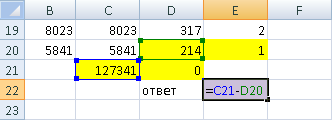
    

11. 
    Для варианта A получаем 127127, для варианта B - 399762080.
    
12. 
    Ответ: 127127 399762080.