метрология. Обработка результатов прямых многократных измерений 1
 Скачать 119.66 Kb. Скачать 119.66 Kb.
|
|
Никулина А.Р ВВБ-004, вариант-30 Таблица 1 – Исходные данные  Обработка результатов прямых многократных измерений 1 Определить среднее арифметическое значение 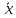 по формуле: по формуле: где хi – i-й результат измерения; n – число исправленных результатов измерений.  м м2 Вычислить среднее квадратическое отклонение S группы, содержащей n результатов измерений по формуле:   м м3 Исключить грубые ошибки (промахи), используя критерий Граббса, сравнивая G1 и G2 с теоретическим значением GT при выбранном уровне значимости q. Для 20 измерений при уровне значимости q (свыше 5 %) GT = 2,709 (табл. 2). Таблица 2 – Критические значения GT для критерия Граббса
G1 и G2 определить по формулам:  , ,    Так как G1 ≤ GT, то xmaxне считаем промахом и сохраняем его в ряде результатов измерений. Так как G2 > GT, то xminисключаем как маловероятное значение. Далее нам необходимо вновь вычислить 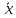 и S и повторить процедуру проверки наличия грубых погрешностей. и S и повторить процедуру проверки наличия грубых погрешностей.1.Определить среднее арифметическое значение 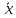 по формуле: по формуле: 2. Вычислить среднее квадратическое отклонение S группы, содержащей n результатов измерений по формуле:   3.Исключить грубые ошибки (промахи), используя критерий Граббса, сравнивая G1 и G2 с теоретическим значением GT при выбранном уровне значимости q. Для 19 измерений при уровне значимости q (свыше 5 %) GT = 2,681 (табл. 2).   Так как G2 > GT, то xminисключаем как маловероятное значение. Так как G1 ≤ GT, то xmax не считаем промахом и сохраняем его в ряде результатов измерений. Далее нам необходимо вновь вычислить 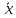 и S и повторить процедуру проверки наличия грубых погрешностей. и S и повторить процедуру проверки наличия грубых погрешностей.1.Определить среднее арифметическое значение 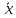 по формуле: по формуле: 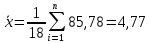 2.Вычислить среднее квадратическое отклонение S группы, содержащей n результатов измерений по формуле:   м м3.Исключить грубые ошибки (промахи), используя критерий Граббса, сравнивая G1 и G2 с теоретическим значением GT при выбранном уровне значимости q. Для 18 измерений при уровне значимости q (свыше 5 %) GT = 2,651 (табл. 2).  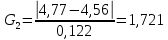 Так как G1 ≤ GT, то xmax не считаем промахом и сохраняем его в ряде результатов измерений. Так как G2 ≤ GT, то xmin не считаем промахом и сохраняем его в ряде результатов измерений. 4. Рассчитать среднее квадратическое отклонение среднего арифметического (оценки измеряемой величины)  по формуле: по формуле:  м м5. Проверить гипотезу о том, что результаты измерений принадлежат нормальному распределению.  Так как m = 0 , следовательно результаты измерений принадлежат нормальному распределению. Определение количества разностей
6. Вычислить доверительные границы случайной погрешности по формуле:  t – коэффициент Стьюдента, зависит от числа степеней свободы и доверительной вероятности (табл. 6). Таблица 6 – Значения коэффициента Стьюдента t
 м м7. 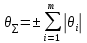  м м5.14 Вычислить доверительные границы погрешности результата измерения по формуле:  где К – коэффициент зависящий от соотношения случайной составляющей погрешности и НСП;  суммарное среднее квадратическое отклонение оценки измеряемой величины, вычисляемое по формуле: суммарное среднее квадратическое отклонение оценки измеряемой величины, вычисляемое по формуле:  м мгде  среднее квадратическое отклонение НСП, которое оценивают по формуле: среднее квадратическое отклонение НСП, которое оценивают по формуле: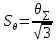  м мКоэффициент К вычисляют по формуле:    5.15 Записать результат измерения При симметричных доверительных границах погрешности результат измерения представляют в форме:   | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||