Образец выполнения практического задания 1. Образец выполнения практического задания 1 Запишем исходные данные расчетной электрической цепи постоянного тока
 Скачать 0.57 Mb. Скачать 0.57 Mb.
|
|
Образец выполнения практического задания № 1 Запишем исходные данные расчетной электрической цепи постоянного тока. Сопротивления резисторов: 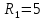 Ом, Ом, 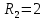 Ом, Ом, 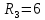 Ом, Ом, 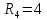 Ом, Ом, 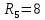 Ом. Значения источников электрической энергии: Ом. Значения источников электрической энергии: 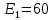 В, В, 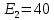 В, В, 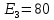 В, В, 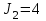 А. А.Конфигурация расчетной электрической цепи изображена на рис. 1. 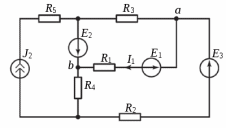 Рис. 1. Расчетная электрическая цепь Решение Определим входное сопротивление активного двухполюсника 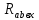 . Преобразуем активную электрическую цепь в пассивную, для этого участки с источниками энергии заменяем на их внутренние сопротивления. В результате получим конфигурацию пассивной электрической цепи (рис. 2) относительно зажимов «a–b». . Преобразуем активную электрическую цепь в пассивную, для этого участки с источниками энергии заменяем на их внутренние сопротивления. В результате получим конфигурацию пассивной электрической цепи (рис. 2) относительно зажимов «a–b».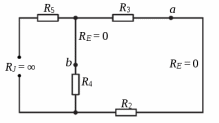 Рис. 2. Нахождение входного сопротивления Видно, что участок цепи с сопротивлениями 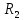 и и 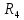 включен последовательно относительно зажимов «a–b» и одновременно этот участок цепи включен параллельно с сопротивлением включен последовательно относительно зажимов «a–b» и одновременно этот участок цепи включен параллельно с сопротивлением 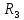 , поэтому можно записать следующее уравнение (формула 1): , поэтому можно записать следующее уравнение (формула 1):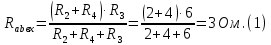 Определим напряжение холостого хода активного двухполюсника 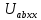 . Для этого необходимо вывести заданную расчетную ветвь в режим холостого хода. Конфигурация расчётной электрической цепи изображена на рис. 3. . Для этого необходимо вывести заданную расчетную ветвь в режим холостого хода. Конфигурация расчётной электрической цепи изображена на рис. 3.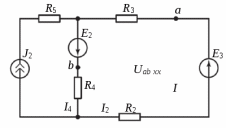 Рис. 3. Нахождение напряжения холостого хода Направим произвольно токи в ветвях и составим уравнение по второму закону Кирхгофа для первого контура в расчётной электрической цепи (рис. 3). Данное уравнение записано в формуле 2: 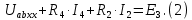 Видно, что неизвестными переменными в этом уравнении являются токи ветвей 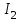 и и 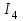 . Найдем значения этих токов по методу контурных токов. Произвольно направим контурные токи, как показано на рис. 4. Причем контурный ток . Найдем значения этих токов по методу контурных токов. Произвольно направим контурные токи, как показано на рис. 4. Причем контурный ток 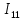 неизвестен, а контурный ток неизвестен, а контурный ток 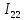 определяется током источника тока определяется током источника тока 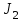 и уже задан. и уже задан.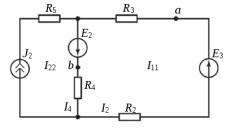 Рис. 4. Расчётная цепь по методу контурных токов Запишем систему уравнений по методу контурных токов (формула 3): 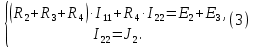 Поскольку контурный ток 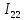 уже задан, то получим значение контурного тока уже задан, то получим значение контурного тока 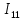 , используя уравнение (формула 4): , используя уравнение (формула 4):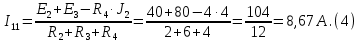 Так как ток ветвей 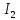 равен контурному току равен контурному току 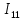 , а ток ветви , а ток ветви 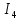 образуется как суперпозиция двух контурных токов образуется как суперпозиция двух контурных токов 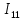 и и 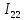 , то напряжение холостого хода определим по следующему уравнению (формула 5): , то напряжение холостого хода определим по следующему уравнению (формула 5):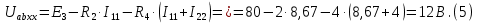 Определим ток первой ветви методом эквивалентного генератора. Изобразим последовательную схему замещения эквивалентного генератора (рис. 5), состоящую из источника ЭДС и внутреннего сопротивления. Первое значение совпадает с напряжением холостого хода активного двухполюсника, а второе – с его входным сопротивлением. 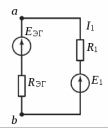 Рис. 5. Расчетная цепь по методу эквивалентного генератора Таким образом, ток первой ветви найдем, составив уравнение по II закону Кирхгофа (формула 6): 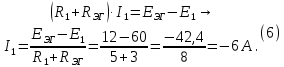 Найденный ток первой ветви получился отрицательным, следовательно, его истинное направление противоположно указанному. Изобразим параллельную схему замещения эквивалентного генератора (рис. 6), состоящую из источника тока и внутренней проводимости, и определим ее параметры. 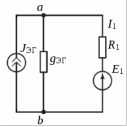 Рис. 6. Расчётная цепь по методу эквивалентного генератора Параметры параллельной схемы замещения определим по формуле 7: 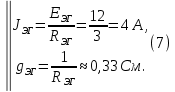 Найдем неизвестные токи ветвей в расчетной электрической цепи методом узловых потенциалов. Примем потенциал узловой точки «4» за нулевое значение (рис. 7). Поскольку сопротивление пятой ветви (с источником ЭДС 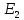 ) равно нулю, то потенциал этой узловой точки уже известен и равен значению источника ЭДС, то есть ) равно нулю, то потенциал этой узловой точки уже известен и равен значению источника ЭДС, то есть 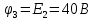 . Таким образом, количество неизвестных потенциалов в расчетной электрической цепи равно двум. . Таким образом, количество неизвестных потенциалов в расчетной электрической цепи равно двум.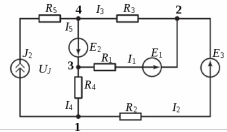 Рис. 7. Расчётная цепь по методу узловых потенциалов Система уравнений по методу узловых потенциалов принимает вид (формула 8): 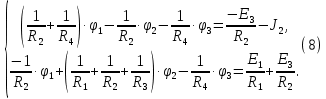 Перенесем слагаемые с потенциалом узловой точки 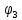 в правую сторону уравнений, подставим числовые значения параметров цепи, тогда получим систему уравнений в виде (формула 9): в правую сторону уравнений, подставим числовые значения параметров цепи, тогда получим систему уравнений в виде (формула 9):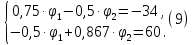 Решая систему уравнений, найдем значения потенциалов узловых точек. Выпишем все известные потенциалы узловых точек расчетной электрической цепи (формула 10): 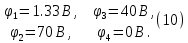 Используем обобщенный закон Ома и выразим токи в ветвях через потенциалы известных значений узловых точек. Данные выражения запишем в формуле 11: 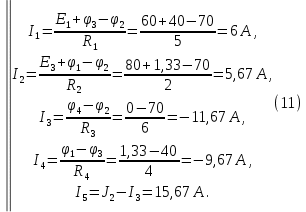 Можем сделать вывод, что ток первой ветви, найденный методом узловых потенциалов, совпадает с ранее найденным методом эквивалентного генератора. Также истинные направления токов в третьей и четвертой ветвях противоположны принятым в расчетной цепи (рис. 8). Ток пятой ветви был найден косвенным путем по I закону Кирхгофа. 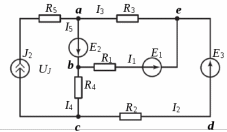 Рис. 8. Истинные токи ветвей в расчетной электрической цепи Составим уравнение баланса мощностей в расчетной электрической цепи. Поскольку количество сопротивлений в расчетной цепи равно пяти, то уравнение мощности приемников также содержит пять слагаемых согласно уравнению (формула 12): 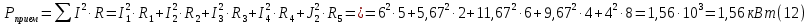 Для нахождения мощности источников предварительно необходимо определить напряжение на источнике тока. Воспользуемся II законом Кирхгофа для контура с источником тока (рис. 8) и запишем уравнение (формула 13): 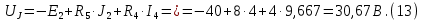 Поскольку количество источников энергии в расчетной цепи равно четырем, то уравнение мощности источников также содержит четыре слагаемых согласно уравнению (формула 14): 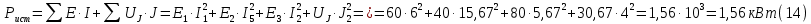 Таким образом, баланс мощности в расчетной электрической цепи выполняется, что говорит о правильности расчета токов ветвей. Рассчитаем потенциалы узловых точек для контура a–b–c–d–e–a. Примем потенциал точки «а» за нуль (рис. 8), тогда значения потенциалов узловых точек найдутся по выражениям (формула 14): 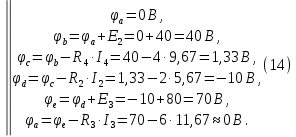 Строим потенциальную диаграмму (рис. 9) на основании расчетных потенциалов узловых точек. 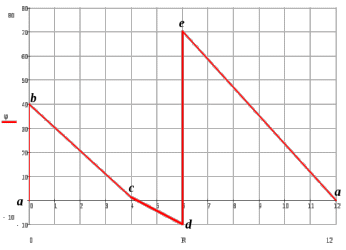 Рис. 9. Потенциальная диаграмма расчетной электрической цепи |
