Практическое задание 1. Алдыбаева А.В.. Образовательная программа 6В06120 Программная инженерия
 Скачать 1.46 Mb. Скачать 1.46 Mb.
|
|
КАСПИЙСКИЙ ОБЩЕСТВЕННЫЙ УНИВЕРСИТЕТ ИНСТИТУТ ГЕОЛОГИИ, НЕФТЕГАОВОГО ДЕЛА и IT Практическое задание №1 «Математика ВО»Образовательная программа – 6В06120 «Программная инженерия» Выполнила: Алдыбаева А.В. Курс: 3 Семестр: 1 Преподаватель: Сейсенбаева А. М. г. Алматы 2020 Вариант 1. Даны матрицы А и В. Найти:а) АВ; ВА; б) 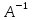 А=В= Ответ: АВ=ВА= 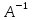 = · = · = 1 0 0 = 1 0 0 2. Проверь совместимость системы уравнений, а если совместим, решите а) Методом Гаусса; б) Методом Крамера; в) матричным способом: 4x – 9y + 5z = 1 7x – 4y + z = 11 3x + 5y – 4z = 5 Ответ: а) Система уравнений не имеет решения, так как 0 ≠ -5 б) Определитель равен 0. Система имеет бесконечное множество решений. в) det A = 0. Таким образом матрица А – вырожденная, то есть система имеет бесконечное множество решений. 3. Используя координат точек А(4,6,3), В(-5,2,6), С(4,-4,-3) , нужно найти а) модуль; б) скалярное произведение; в) смешанное произведение векторов. а) модуль a ≈ 7.81 b ≈ 8.06 c ≈ 6,40 б) a·b = 10 b·c = - 46 a·c = - 17 в) B = 4·2·(-3)-4·6·(-4)-4·3·2 = 162 Поскольку определитель больше 0, то векторы образуют правую систему. 4. Даны вершины пирамиды А(3,4,5), В(1,2,1), С(-2,-3,6), D(3,-6,-3). Вычислить: а) площадь стороны АСD; б) площадь сечения проходящего через l=АВ грань и вершины С и D; в) объем пирамиды. Ответ: а) S ACD = 45,978 (кв.ед) б) S = 39,29 (кв.ед) в) V = 42 (кв.ед) 5. Даны точки  (3,1,4) , (3,1,4) , 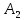 ( 1,6,1), ( 1,6,1),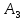 ( 1,1,6), ( 1,1,6),  (0,4, 1), составьте уравнение: а) (0,4, 1), составьте уравнение: а)плоскости 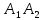 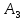 , б) прямой , б) прямой 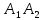 ; в) прямой ; в) прямой  M перпендикулярно плоскости M перпендикулярно плоскости 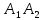  ; г) прямой ; г) прямой  N параллельно прямой N параллельно прямой  ; д) плоскости перпендикулярно прямой ; д) плоскости перпендикулярно прямой  , проходящей через точку , проходящей через точку  . .Ответ: а) x + 2y + 2z – 13 = 0 б) Каноническое: 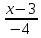 = = 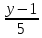 = = 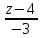 Параметрическое: x = 3 – 4t y = 1 + 5t z = 4 – 3t в)  M = M = 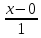 = =  = =  г)  N = N =  = =  = = 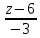 д) – 4x + 5y – 3z +19 = 0  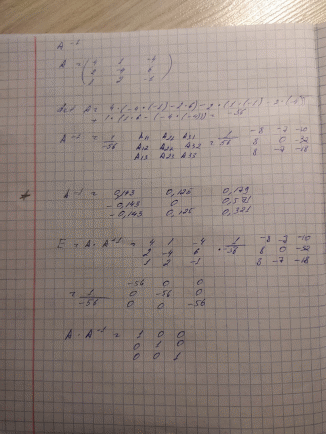 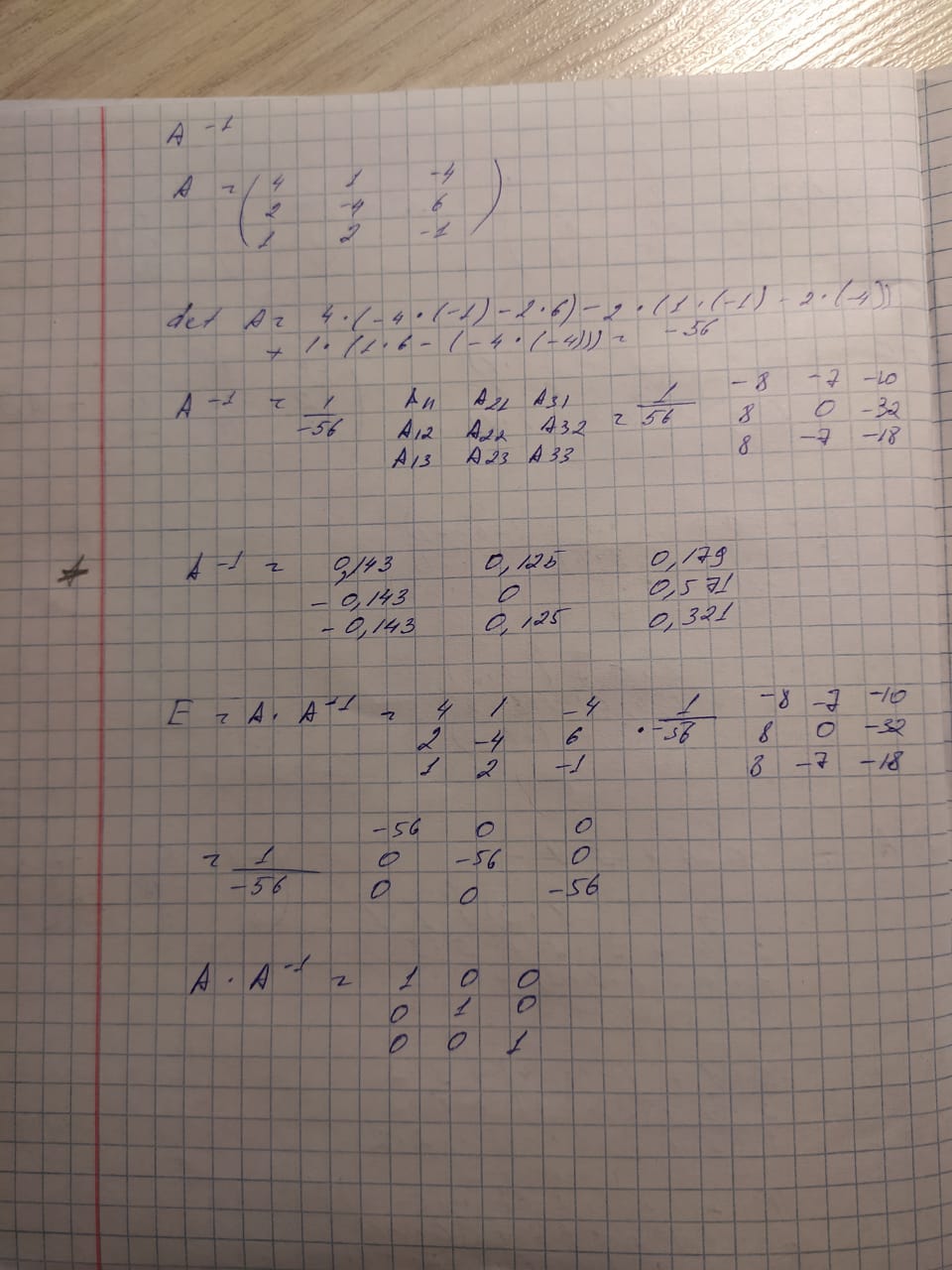 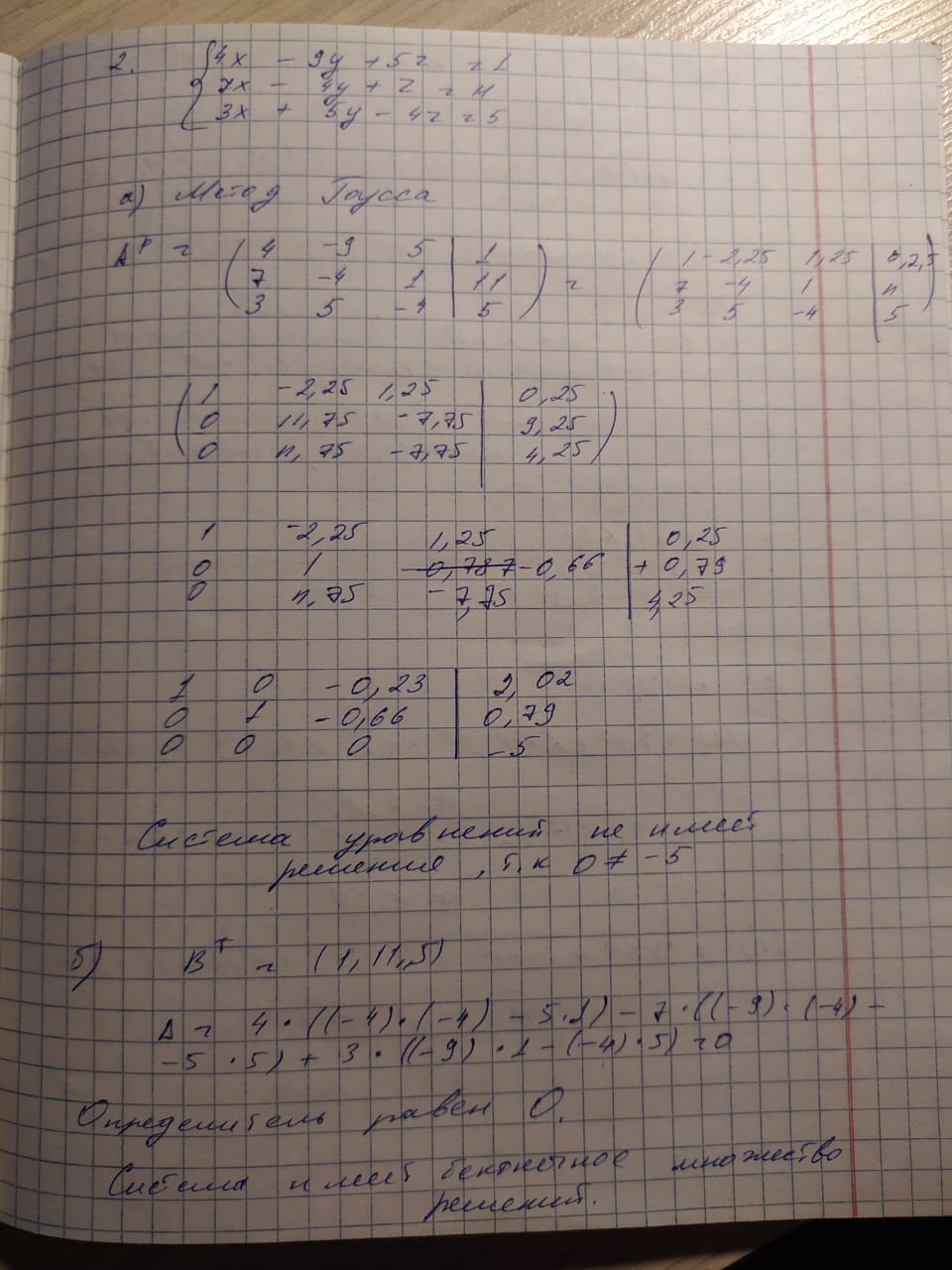  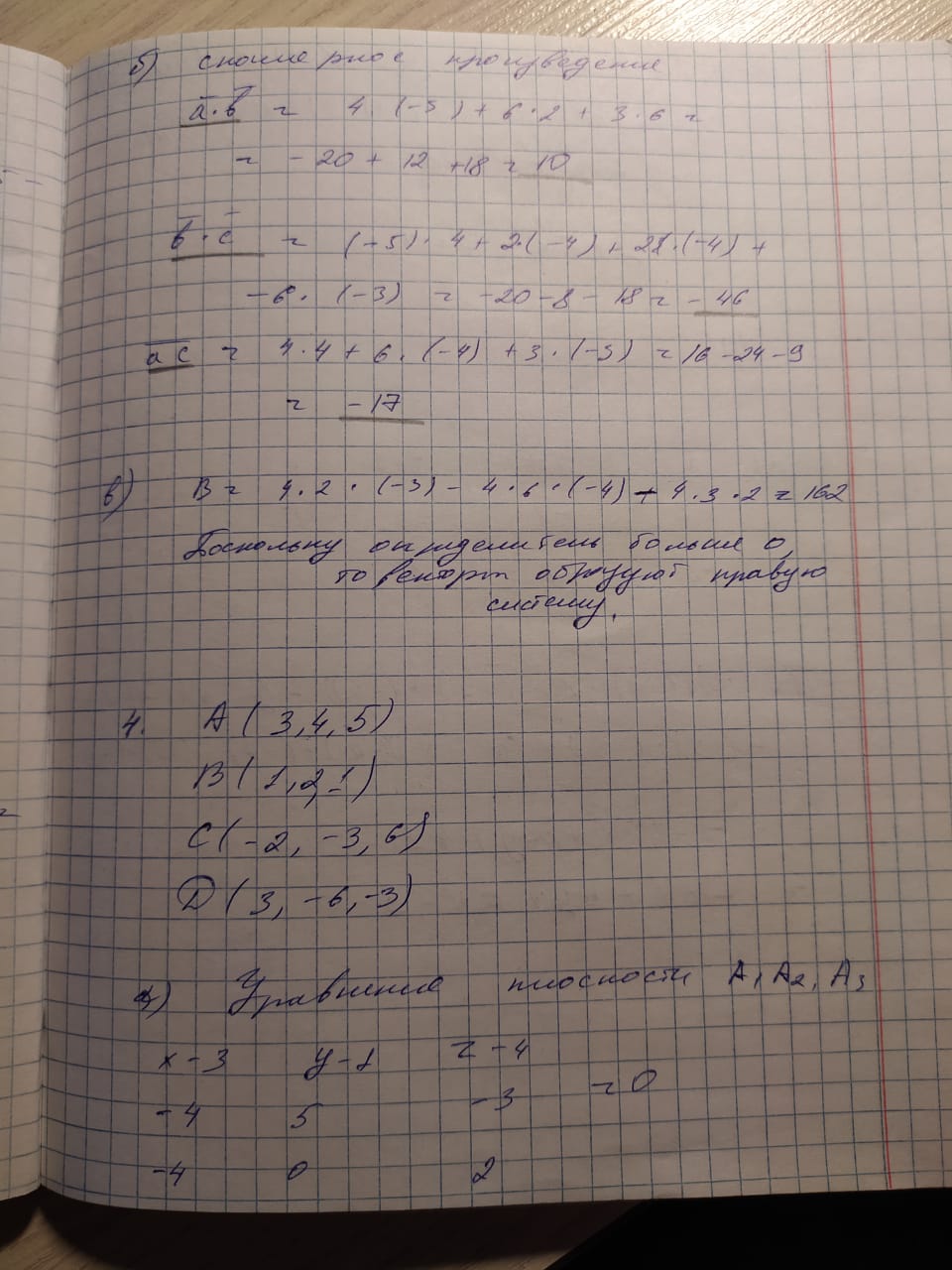     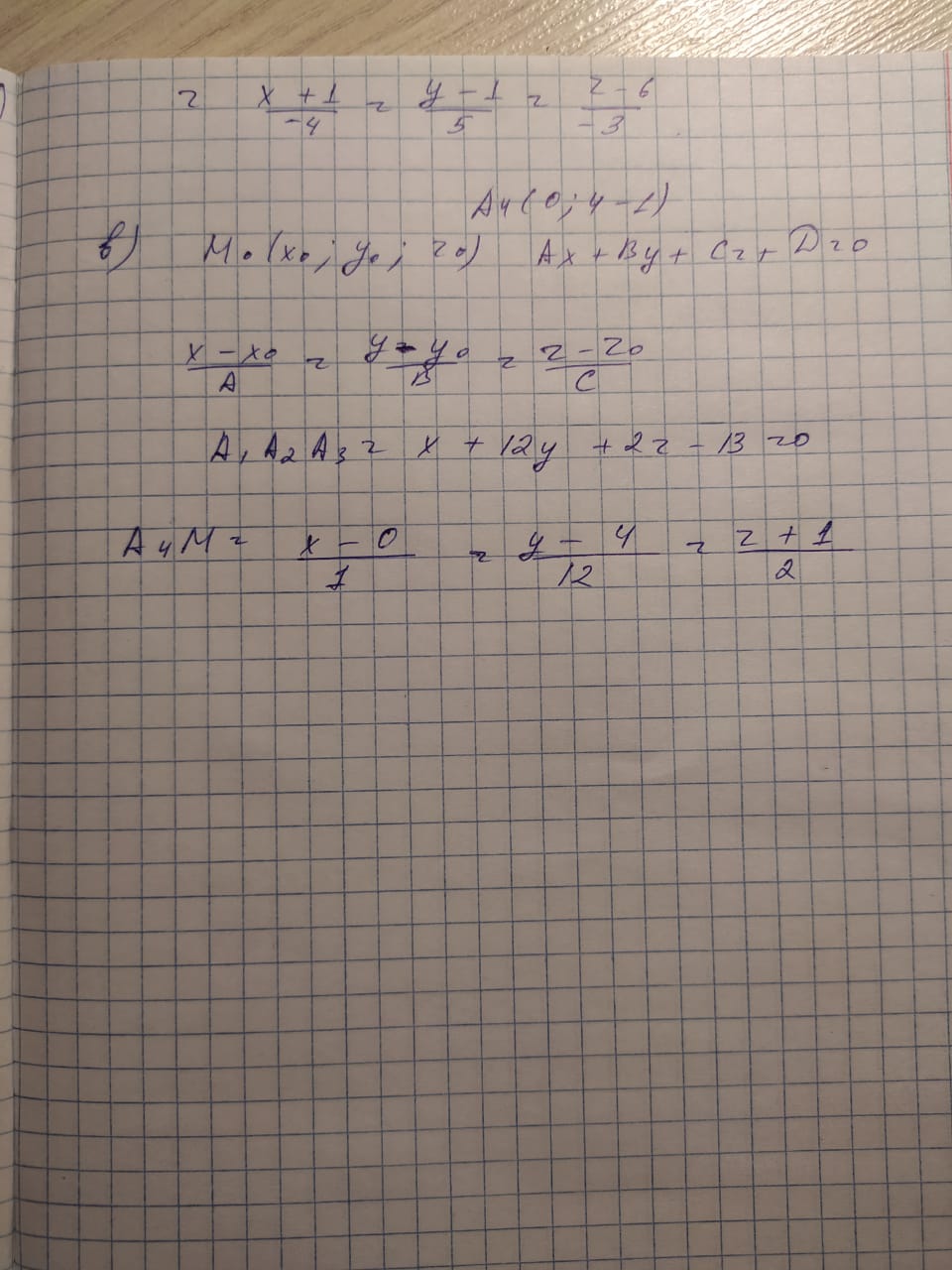 |
