Информационное обеспечение, программирование. Обрунтування вибору методу та алгоритм розвязання задачі. Опис математичної моделі задачі
 Скачать 1.15 Mb. Скачать 1.15 Mb.
|
|
Зміст Вступ 1. Постановка задачі 2. Обґрунтування вибору методу та алгоритм розв’язання задачі . Опис математичної моделі задачі . Інтерфейс програми . Лістинг програми . Контрольний приклад Список використаної літератури Вступ Оптимiзацiя в широкому значеннi слова знаходить застосування в науцi, технiцi i у будь-який iншiй областi людської дiяльностi. Оптимiзацiя - цiлеспрямована дiяльнiсть, що полягає в одержаннi найкращих результатiв при вiдповiдних умовах. Пошуки оптимальних розв'язкiв привели до створення спецiальних математичних методiв i вже в 18 столiттi були закладенi математичнi основи оптимiзацiї (варiацiйне числення, чисельнi методи й iншi). Однак до другої половини 20 столiття методи оптимiзацiї в багатьох областях науки i технiки застосовувалися дуже рiдко, оскiльки практичне використання математичних методiв оптимiзацiї вимагало величезної обчислювальної роботи, що без ЕОМ реалiзувати було вкрай важко, а в рядi випадкiв - неможливо. Особливо великi труднощi виникали при розв'язку задач оптимiзацiї процесiв у хiмiчнiй технологiї через велике число параметрiв i їхнього складного взаємозв'язку мiж собою. При наявностi ЕОМ задачi помiтно спрощуються. Постановка задачi оптимiзацiї припускає iснування конкуруючих властивостей процесу, наприклад: кiлькiсть продукцiї - "витрата сировини" кiлькiсть продукцiї - "якiсть продукцiї" Вибiр компромiсного варiанта для зазначених властивостей i являє собою процедуру розв'язку оптимiзацiйнної задачi. При постановцi завдання оптимiзацiї необхiдно: Наявнiсть об'єкта оптимiзацiї i мети оптимiзацiї. При цьому формулювання кожної задачi оптимiзацiї повинно вимагати екстремального значення лише одного розміру, тобто одночасно системi не повинно приписуватися два i бiльш критерiїв оптимiзацiї, тому що практично завжди экстремум одного критерiю не вiдповiдає экстремуму iншого. 1. Постановка задачі Необхідно знайти найкоротшу відстань і маршрут від заводу збірного залізобетону, що знаходиться в пункті 1 до будівельних майданчиків 2-9 при заданій схемі автомобільних шляхів (рис.1). Знайти також найкоротший шлях холостого пробігу машин за умови, що частина доріг має односторонній напрямок руху (вказано стрілками на схемі). 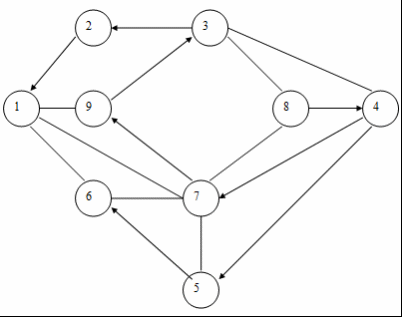 2. Обгрунтування вибору методу та алгоритм розв’язання задачі В даній задачі стоїть завдання знайти найкоротшу відстань і маршрут від заводу збірного залізобетону до будівельних майданчиків, а це є алгоритм Дейкстри (задача про найкоротший ланцюг). Алгоритм знаходження найкоротшої відстані ґрунтується на тому, що даний граф представляється у вигляді матриці суміжності G[n,n], де n - кількість вершин в графі. Якщо існує шлях із i-ї вершини в j-ту, і вартість цього шляху складає х, то записується G[i,j]=x. Якщо шляху не існує, то х дорівнює нескінченості. Для знаходження найкоротшого шляху застосовуємо алгоритм Дейкстри. Вирішення цієї задачі (за алгоритмом Дейксти) базується на наступному принципі: якщо відомо найкоротший ланцюг з Х в Y і на цьому ланцюзі знаходиться вершина Z, то найкоротший ланцюг з XZ співпадає з ZY .  3. Опис математичної моделі Графом G(V,E) називається сукупність двох множин - не порожньої множини V (множини його вершин) та множини Е невпорядкованих пар елементів в множині V, Е - множина ребер графа. Маємо орієнтований граф G=(V,E), кожній дузі v->w цьго графа зіставлена невід’ємна віртість C[v,w]. Загальна задача знаходження найкоротших шляхів полягає у знаходженні для кожної впорядкованої пари вершин (v,w) будь-якого шляху від вершини v у вершину w, довжина якого найкоротша з усіх можливих. Матриця суміжностей графа G(V,E) - це квадратна матриця, елементи якої визначаються так:  Основою розв’язання даної задачі є алгоритм Дейкстри, загальна рекурентна форма якого: Ak[i,j]=min(Ak-1[i,j], Ak-1[i,k]+Ak-1[k,j]). Якщо від вершини i до j не існує ребра то G[i,j]=∞ // нескінченість G` - граф мінімальних вартостей G* - граф найкоротших проміжних шляхів. Інтерфейс даної програми містить можливість введення змінної кількості вершин і ребер, оптимальне використання ресурсів пам’яті комп’ютера і часу виконання. Передбачає відслідковування введення некоректних даних, виключних ситуацій, можливість збереження результатів виконання програм у файл, містить коротку довідку користування програми і використаних алгоритмів. 4. Інтерфейс програми 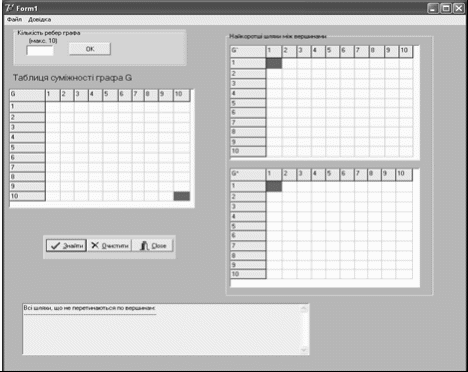 5. Лістинг програми unit Unit1;, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,, Grids, StdCtrls, Buttons, Menus, ExtCtrls;= 20;= maxint div 2;= class(TForm): TStringGrid;: TLabel;: TMainMenu;: TMenuItem;: TMenuItem;: TMenuItem;: TMenuItem;: TMenuItem;: TMenuItem;: TGroupBox;: TStringGrid;: TStringGrid;: TGroupBox;: TLabel;: TEdit;: TBitBtn;: TPanel;: TSpeedButton;: TBitBtn;: TBitBtn;: TMemo;FormCreate(Sender: TObject);BitBtn3Click(Sender: TObject);init(sender: tobject);floyd;N3Click(Sender: TObject);Clear(Sender: TObject);N2Click(Sender: TObject);path(i, j: integer);N6Click(Sender: TObject);N5Click(Sender: TObject);, a: array [1..maxn, 1..maxn] of integer;: array [1..maxn, 1..maxn] of integer;: longint;: string; { Public declarations };: TForm1;Unit4, Unit2, Unit3; {$R *.dfm}TForm1.FormCreate(Sender: TObject);i,j: longint;i:=1 to G.ColCount doj:=1 to G.ColCount do begin.Cells[i,j]:=' ';.Cells[i,j]:=' ' end;.Cells[0,0]:='G';.Cells[0,0]:='G*';.Cells[0,0]:='G`';i:=1 to 10 do begin.Cells[0,i]:=IntToStr(i);.Cells[0,i]:=IntToStr(i);.Cells[0,i]:=IntToStr(i);.Cells[i,0]:=IntToStr(i);.Cells[i,0]:=IntToStr(i);.Cells[i,0]:=IntToStr(i); //Cells[i,i]:='0';; //for; //procedureTForm1.BitBtn3Click(Sender: TObject);:=StrToInt(Edit1.Text);(n>0) and (n<=10) then begin.Enabled:=True;.Enabled:=True;.Enabled:=true end('Невірні дані',MtError,[mbOk],0);;TForm1.init(sender: tobject);, j, x, y, nn, z: longint;.Enabled:=true;i := 1 to maxn doj := 1 to maxn do[i, j] := inf;i := 1 to maxn do[i, i] := 0;(d, sizeof(d), 0);(p, sizeof(p), 0);:=StrToInt(Edit1.Text);i:=1 to n doj:=1 to n doG.Cells[i,j][1] in ['0'..'9'] then[i,j]:=StrToInt(G.Cells[i,j]);;;TForm1.floyd;, i, j: integer;i := 1 to n doj := 1 to n do[i, j] := i;[i, j] := a[i, j];;k := 1 to n doi := 1 to n doj := 1 to n dod[i, j] > d[i, k] + d[k, j] then[i, j] := d[i, k] + d[k, j];[i, j] := k;;i:=1 to n doj:=1 to n do beginp[i,j]=i then p[i,j]:=0;.Cells[i,j]:=IntToStr(p[i,j]);d[i,j]>=1000 then G2.Cells[i,j]:='#' else.Cells[i,j]:=IntToStr(d[i,j]) end;i:=1 to n doj:=1 to n do(p[i,j]=0) and (g.Cells[i,j][1] in ['1'..'9']) then.Lines.Add(IntToStr(j)+'-->'+IntToStr(i));.Lines.Add('Всі шляхи, що не перетинаються по ребрам');.Lines.Add('--------------------------------------------------------------------------------');i:=1 to n doj:=1 to n do begin:='';G2.Cells[i,j][1] in ['1'..'9'] then begin(j,i);.Lines.Add(IntToStr(i)+'-->'+str+IntToStr(j)); end; end;;TForm1.N3Click(Sender: TObject);;;TForm1.Clear(Sender: TObject);i,j: longint;i:=1 to G.ColCount doj:=1 to G.ColCount do begin.Cells[i,j]:=' ';.Cells[i,j]:=' ';.Cells[i,j]:=' ' end;.Lines.Clear;.Lines.Add('Bсі шляхи, що не перетинаються по вершинам:');.Lines.Add('--------------------------------------------------------------------------------');;TForm1.N2Click(Sender: TObject);f: textFile;,j: integer;.Show;(f, SaveDlg.LEdit1.Text);(f);(f);(f,'Таблиця суміжності графа G');i:=1 to n do beginj:=1 to n do(f,G.Cells[i,j],' ');(f) end;(f);(f,'Найкоротші шляхи графа G');i:=1 to n do beginj:=1 to n do(f,G2.Cells[i,j],' ');(f) end;(f);; procedure TForm1.path(i, j: integer);k: integer;:= P[i,j];k=0 then exit;(i,k);:=str+' '+IntToStr(k)+'-->';(k,j);;TForm1.N6Click(Sender: TObject);.Show;;TForm1.N5Click(Sender: TObject);.show;;. алгоритм математичний лістинг програма 6. Контрольний приклад Для заданого графу, що зображений на Рис.1 заповнюємо таблицю суміжності у відповідності до завдання, враховуючи те, що в ньому присутні деякі орієнтовані дуги. 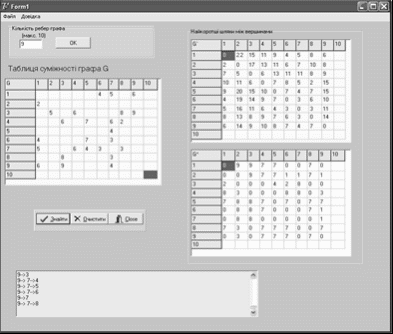 В результаті ми отримуємо дві матриці - матрицю мінімальних відстаней між заводом залізобетону та будівельними майданчиками: 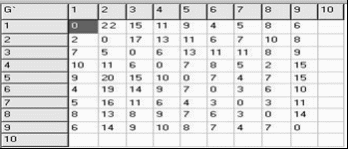 Враховуючи те, що деяка частина доріг має односторонній напрямок руху, для прикладу наведемо такі данні: · Найкоротша відстань від пункту 1 (завод ЗБК) до пункту 2 (буд. майданчик )становить 22 , проте якщо ми будемо рухатись від пункту 2 до пункту 1, відстань між ними буде становити 2. · Найкоротша відстань від пункту 1 (завод ЗБК) до пункту 3 (буд. майданчик )становить 15, проте якщо ми будемо рухатись від пункту 3 до пункту 1, відстань між ними буде становити 7. і т.д. · Найкоротша відстань від пункту 1 (завод ЗБК) до пункту 4 (буд. майданчик ) становить 10, проте якщо ми будемо рухатись від пункту 4 до пункту 1, відстань між ними збільшиться і буде становити 11. · Найкоротша відстань від пункту 1 (завод ЗБК) до пункту 5 (буд. майданчик ) становить 9. · Найкоротша відстань від пункту 1 (завод ЗБК) до пункту 6 (буд. майданчик ) становить 4. · Найкоротша відстань від пункту 1 (завод ЗБК) до пункту 7 (буд. майданчик ) становить 5. · Найкоротша відстань від пункту 1 (завод ЗБК) до пункту 8 (буд. майданчик ) становить 8. · Найкоротша відстань від пункту 1 (завод ЗБК) до пункту 9 (буд. майданчик ) становить 6. В результаті роботи програми формується ще одна матриця- матриця найкоротших проміжних шляхів: 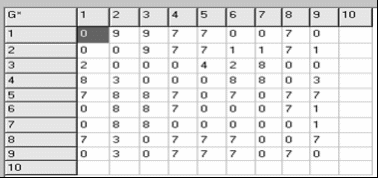 Тут вказуються проміжні пункти від заводу ЗБК (тобто пункту 1), через який можна потрапити до потрібного будівельного майданчику. Наприклад, якщо рухатись від 1 до 2 пункту, то проміжним для них буде пункт 9. Проте враховуючи односторонній напрямок руху деяких доріг рухаючись від 2 до 1 проміжного пункту між ними не існує, тому відповідь програми - 0 . · Проміжним пунктом між 1 та 3 є пункт 9, проте рухаючись з 3 в 1 проміжним пунктом є 2. · Проміжним пунктом між 1 та 4 є пункт 7, проте рухаючись з 4 в 1 проміжним пунктом є 8. · Проміжним пунктом між 1 та 5 є пункт 7. · Проміжного пункту між 1 та 6 , а також 1 та 7 не існує. · Проміжним пунктом між 1 та 8 є пункт 8. · Проміжного пункту між 1 та 9 не існує. Список використаної літератури 1. Фиакко А., Мак-Кормик Г. Нелинейное программирование. Методы последовательной безусловной минимизации. - М.: Мир, 1972. 2. Сухарев А.Г., Тимохов А.В., Федоров В.В. Курс методов оптимизации. - М.: Наука, 1986. 3. Акулич И.Л. Математическое программирование в примерах и задачах. М.: Высшая школа, 1986. |
