Экономические задачи. Общая схема решения экономических задач
 Скачать 490.58 Kb. Скачать 490.58 Kb.
|
|
ГЛАВА 4. РАСЧЕТ БАНКОВСКИХ КРЕДИТОВ. ВЫВОД ФОРМУЛ. В этом разделе будут рассмотрены задачи на вычисления связанные с кредитованием, а именно нахождение: процентной ставки, суммы долга, суммы переплаты, ежегодных (ежемесячных, еженедельных т.д.) выплат, количество лет. Данные подсчеты экономически целесообразны в связи с тем, что каждый человек при заключении договора определяет наиболее выгодные для себя условия. Такие задания классифицируются на простые, решения которых ограничиваются одной формулой, и сложные решение которых требует составления систем, решение неравенств и т.д. Для многих задач данного типа удобно использовать формулы, выведение которых представлено ниже. Рассмотрим основные элементы, которые встречаются в задачах, и дадим им характеристику: S – сумма, которую берут в кредит r – годовая/месячная ставка k – число, показывающее во сколько раз увеличивается сума S перед банком (k = 1+0,01*r) x - выплата n– количество лет/месяцев, за которое необходимо выплатить кредит F – сумма, которую в итоге придется вернуть банк P – переплата, равная F - S 4.1. Вывод формул для решения задач на равные размеры выплат. Первая формула на нахождение суммы долга, обычно в задачах условия кредитования следующие: в банке берется кредит и увеличивается на rпроцентов, затем вносится выплата, и сумма оставшегося долга увеличивается на rпроцентов, и так через n лет происходит погашение кредита. Задача1. [6] В июле планируется взять кредит на сумму 6 409 000 рублей. Условия его возврата таковы: - каждый январь долг возрастает на 12,5% по сравнению с концом предыдущего года; - с февраля по июнь каждого года необходимо выплатить некоторую часть долга. Сколько рублей нужно платить ежегодно, чтобы кредит был полностью погашен двумя равными платежами (то есть за два года)? Решение. Составим краткую запись: S = 6 409 000 рублей r = 12, 5% k = 1+0,01r = 1,125 = 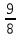 х = ? рублей n = 2 года 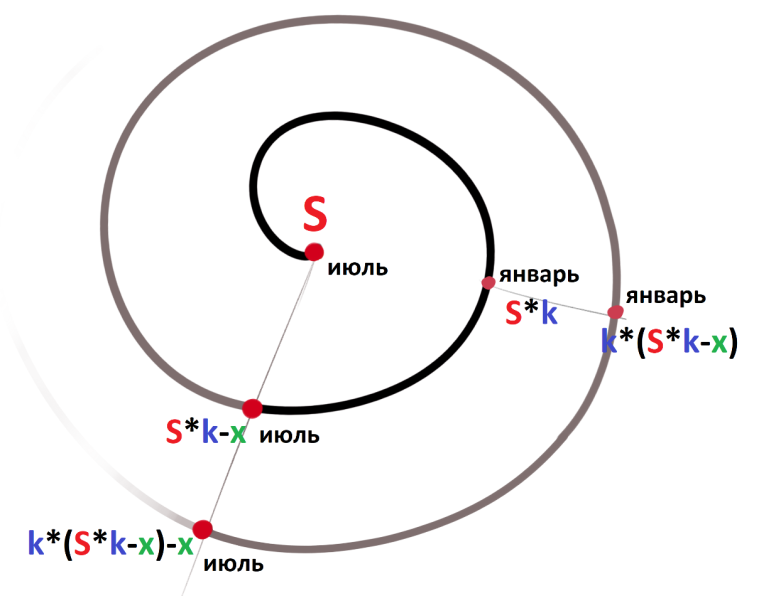 Проиллюстрируем процесс кредитования на спирали: Проиллюстрируем процесс кредитования на спирали:Заметим, что кредитование похоже на цикл, в котором можно выделить три этапа: долг перед банком, выплата, остаток. Перенесем все данные в таблицу. Перенесем данные в таблицу:
Составим уравнение, где последний остаток равен нулю, чтобы узнать размер выплаты 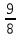 * (6 409 000 * * (6 409 000 *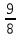 -x) – x = 0 -x) – x = 06 409 000 * 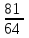 - - 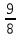 х – х = 0 х – х = 0- 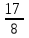 х = - х = - 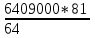 x = 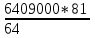 * *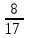 x = 3 817 125 (рублей) Ответ: 3 817 125 рублей Рассмотрим вторую задачу такого же типа. Задача 2. [6] В июле планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы: - каждый январь долг возрастает на 20% по сравнению с концом предыдущего года; - с февраля по июнь каждого года необходимо выплатить часть долга, равную 2,16 млн рублей Сколько млн рублей было взято в банке, если известно, что он был полностью погашен тремя равными платежами (то есть за три года)? Решение. Так же запишем краткую запись: S = ? млн рублей r = 20% k = 1, 2 x = 2, 16 млн рублей n = 3 года
Раскроем скобки
Sk3-k2x - kx – x = 0 Sk3 =k2x + kx + x Sk3 = х (k2+ k + 1) (сделаем замену числа k) S*1, 23 =х (1,22+ 1,2 + 1) (сделаем замену числа х) S = 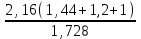 S = 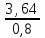 S = 4, 55 (млн рублей) Ответ: 4,55 млн рублей Заметим, что обе задачи решаем по одной схеме. Различия в том, что в первой задаче ищем размер выплат, а во второй задаче – сумму, взятую в кредит. В обеих задачах приходим к одной формуле. Задача 1. k(Sk-x)-x=0(последний остаток равен 0) , отсюда 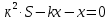 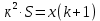 С этого момента можем получить две формулы. 1. 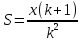 2. 2. 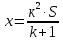 Задача 2. 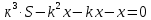 (последний остаток равен 0) , отсюда (последний остаток равен 0) , отсюда 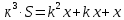 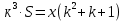 С этого момента можем получить две формулы. 1. 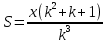 2. 2. 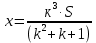 Задача 3. [5] 31 декабря 2014 года Алексей взял в банке 9 282 рублей в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Алексей переводит в банк X рублей. Какой должна быть сумма X, чтобы Алексей выплатил долг четырьмя равными платежами (то есть за четыре года) Решение. Снова нарисуем спираль. 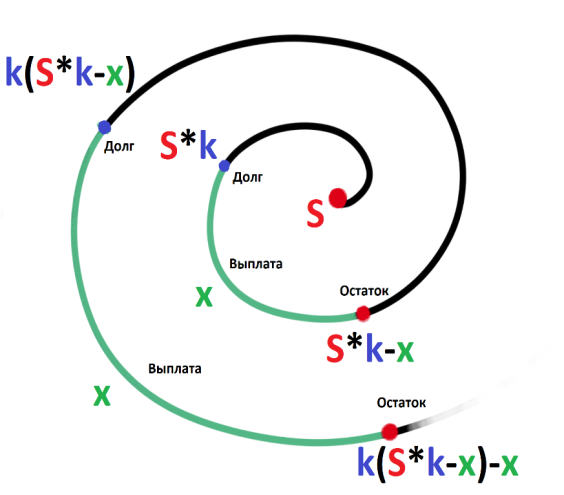 Решение. Краткая запись: S = 9 282 000 млн r = 10% (годовые) k = 1+0,01r = 1 + 0,01*10 =1,1 n = 4 года х =? рублей
Раскроем скобки
*Примечание: на основании этой таблицы, можно вывести формулу KnS – kn-1x – kn-2x – kn-3x - …. - kx –x = 0 Составим уравнение, где последний остаток равен нулю. k4S-k3x - k2x - kx-x = 0 (подставим вместо k число 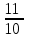 ) )( 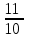 )4S = x(( )4S = x((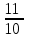 )3 + ( )3 + (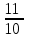 )2 + )2 + 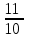 + 1) + 1)( 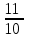 )4S = x ( )4S = x (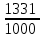 + + 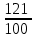 + + 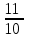 + 1) + 1)( 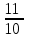 )4S = x )4S = x 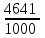 114*S÷104 = 4641x÷103 4641x*104 = 114S*103 x = 114S*103 ÷ 4641*104 (заменим S на 9 282 000) 12 x = 14 641 * 9 282 000 ÷ 4641 x = 2 928 200 Ответ: 2 928 200 рублей Второй способ решения задачи. Назовем эти задачи А) Задачи на равный размер выплат. Зная, что мы долг должны погасить четырьмя равными платежами запишем формулу последнего остатка k4S-k3x - k2x - kx-x = 0. Отсюда выведем k4S=k3x + k2x + kx+x . 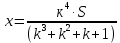 ; Если бы мы искали S, то получили бы формулу ; Если бы мы искали S, то получили бы формулу 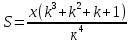 ; ; На основании решений задач 1, 2, 3 запишем формулы 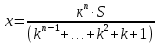 ; ; 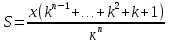 ; ;Решение задач на сокращение остатка на одну долю от целого. Следующий тип задач назовем тип Б) Задачи на сокращение остатка на одну долю от целого Пример решения задачи типа Б: Задача 4. [5] 15 января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы: - 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца; - со 2-го числа пло14-е число каждого месяца необходимо выплатить часть долга; - 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца. 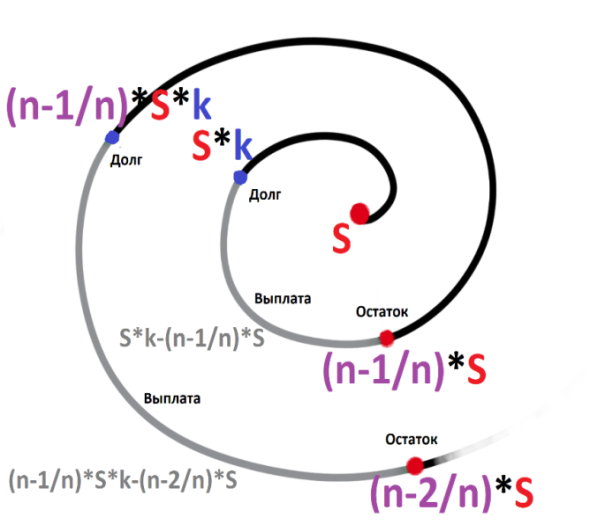 Известно, что в течение первого года кредитования нужно вернуть банке 466,5 тыс. рублей. Какую сумму планируется взять в кредит? Известно, что в течение первого года кредитования нужно вернуть банке 466,5 тыс. рублей. Какую сумму планируется взять в кредит?Решение. Краткая запись: S =? рублей r = 3% k = 1+0,01*3 = 1,03 Сумма x за 12 месяцев = 466,5 тыс. рублей n = 24 месяца С каждым месяцем долг будешь уменьшаться в 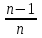 , , 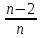 …. …. 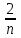 , ,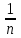 , 0 , 0
Составим уравнение, где сумма всех выплат будет равняться всем выплатам за год кредитования. Найдем сумму кредита. S(k-1)*(1 + 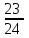 + + 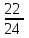 + +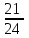 + +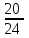 + +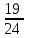 + +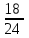 + +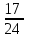 + +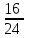 + +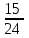 + +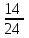 + +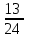 ) + ) + 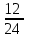 S = 466 500 S = 466 500S(k-1)* 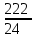 + + 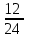 S = 466 500 (заменим число k на 1,03) S = 466 500 (заменим число k на 1,03)S(1,03-1)* 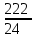 + + 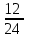 S = 466 500 S = 466 500S*(0,03* 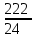 + + 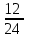 ) = 466 500 ) = 466 500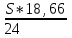 = 466 500 = 466 500S = 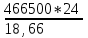 S = 600 000 (рублей) Ответ: 600 000 рублей Запишем общую формулу для решения данной задачи. 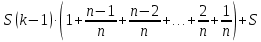 -сумма выплат -сумма выплатПрименим ее для решения следующей задачи. Задача 5. [3] 15-го января планируется взять кредит в банке на 19 месяцев. Условия его возврата таковы: - 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца; - со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; - 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит. Найдите r. Решение. 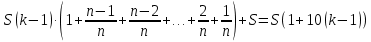 . .Подставим в формулу наши данные, получим 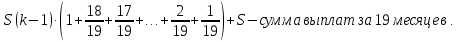 Сгруппируем 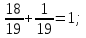 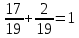 ; ;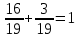 ; ;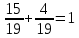 ; ;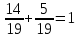 ; ;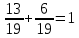 ; ; 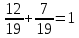 ; ;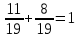 ; ;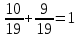 . .Получим 9 пар по 1. Поэтому 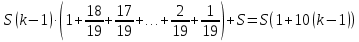 . .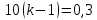 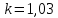 Ответ: 3% Ответ: 3%Задача 6. [4] В июле планируется взять кредит на сумму 18 млн. рублей на некоторый срок(целое число лет). Условия его возврата таковы: -каждый январь долг возрастает на 10 % по сравнению с концом предыдущего года; -с февраля по июнь каждого года необходимо выплатить часть долга; -в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года. На сколько лет планируется взять кредит , если известно, что общая сумма после выплат после его погашения составит 27 млн. рублей. Решение. Снова обратимся к той же формуле 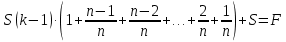 F-сумма выплаченная банку, P-переплата 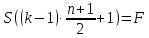 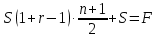 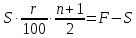 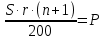 Подставив в эту формулу найдем 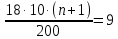 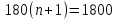 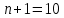 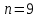 Ответ: 9 лет. Рассмотрим ещё несколько задач. Задача 7.[5] 15-ого января Аркадий планирует взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата следующие: - 1-ого числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r - целое число; - выплата должно производиться один раз в месяц со 2-ого по 14-е число каждого месяца; - 15-ого числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
Найдите наименьшее значение r, при котором Аркадию в общей сумме придется выплатить больше 1,5 млн рублей. 15
Теперь составим неравенство, где сумма всех выплат будет строго больше 1,5 млн: k – 0,8 + 0,8k - 0,6 + 0,6k – 0,5 + 0,5k – 0,4 + 0,4k – 0,3 + 0,3k – 0 > 1,5 3,6k – 2,6 > 1,5 3,6k > 4,1 3,6(1+0,01r) > 4,1 3,6 + 0,036r > 4,1 0,036r > 0,5 r > 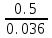 r> 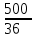 r > 13,8(3) => r = 14 Ответ: 14% Задача 8. .[4] В июле 2020 года планируется взять кредит на некоторую сумму. Условия возврата таковы: - в январе каждого года долг увеличивается на 30% по сравнению с предыдущим годом - с февраля по июнь нужно выплатить часть долга одним платежом. Определите, на какую сумму взяли кредит в танке, если известно, что кредит был выплачен тремя равными платежами (за 3 года) и общая сумма выплат на 156 060 рублей больше суммы взятого кредита. Краткая запись: S = ? рублей r = 30% k = 1, 3 = 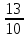 x = ? рублей (равные платежи) n = 3 года F = S+ 156 060 рублей
Составим уравнением с последним остатком, чтобы определить размер суммы S: Sk3-k2x - kx – x = 0 Sk3 = k2x + kx + x Sk3 = х (k2 + k +1) Sk3 = x(( 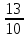 )2+ )2+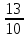 + 1) + 1)Sk3 = x ( 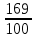 + + 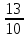 + + 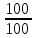 ) )Sk3 = 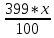 Sk3 * 100 = 399*х S = 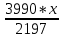 Определим размер выплаты: 3х = 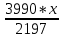 + 156 060 + 156 060 6591х = 3990*х + 342 863 820 2601х = 342 863 820 х = 131 820 Возвращаясь к уравнению из пункта 1, найдем теперь размер суммы S: S = 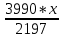 S = 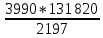 S = 3990 * 60 S = 239 400 (рублей) Общая схема решения экономических задач. Решив и проанализировав задачи, я пришла к заключению, что большая часть задач сводится к таблице такого вида:
Для понимания задачи всегда можно нарисовать спираль. Таким образом, в ходе своего исследования я заметила: I. что большинство экономических задач можно условно разделить на два типа: А) равный размер выплат Б) сокращение остатка на одну долю от целого. II. имеет общую схему решения: 1.Нарисовать процесс «движения» денег в виде спирали 2. Занести данные в таблицу 3. Составить выражения для всех столбиков таблицы 4. Составить уравнение или неравенство 5. В ходе решения уравнения появится формула, с помощью которой будет найдено неизвестное Формулы экономических задач, которые получены в ходе моего исследования А) равный размер выплат Основная идея для решения этих задач уравнение для последнего остатка: KnS – kn-1x – kn-2x – kn-3x - …. - kx –x = 0 Из этого уравнения выводим формулы для S и X. 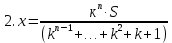 ; ; 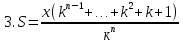 ; ;Б) сокращение остатка на одну долю от целого. Закономерность изменения выплата при её разном значении: 1.S(k-1)+ 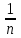 S; S; 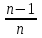 *S(k-1)+ *S(k-1)+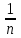 S; S;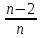 *S(k-1)+ *S(k-1)+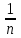 S; … S; … 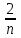 *S(k-1)+ *S(k-1)+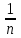 S; S;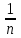 *S(k-1)+ *S(k-1)+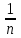 S S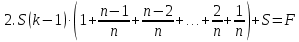 сумма выплат сумма выплатФормула переплаты: 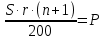 (где P = F – S) (где P = F – S) |

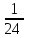 S
S