электрические машины. Глава 6-10. Общие вопросы теории бесколлекторных машин

• Название: Общие вопросы теории бесколлекторных машин
• Анкор: электрические машины
• Дата: 19.09.2022
• Размер: 3.01 Mb.
• Имя файла: Глава 6-10.doc
• Тип: Документы; #684787
• страница: 3 из 7

Контрольные вопросы

1. 
   Объясните принцип действия генератора переменного тока.
   
2. 
   Чем определяется форма графика ЭДС синхронного генератора?
   

3. Каково назначение контактных колец и щеток в синхронном генераторе?

4. Объясните принцип действия асинхронного двигателя.

5. Может ли ротор асинхронного двигателя вращаться синхронно с вращаю­щимся полем?

6. Какие функции выполняет обмотка статора в синхронном генераторе и в асинхронном двигателе?

ГЛАВА 7

• Принцип выполнения обмоток статора
§ 7.1. Устройство статора бесколлекторной машины и основные понятия об обмотках статора

Статор бесколлекторной машины переменного тока (рис. 7.1) состоит из корпуса 1, сердеч-ника 2 и обмотки 3. Сердечник статора имеет шихтованную конструкцию, т. е. представляет собой пакет пла­стин, полученных методом штамповки из листовой электротехнической стали. Пластины предваритель­но покрывают с двух сторон тонкой изоляционной пленкой, например слоем лака. На внутренней по­верхности сердечника статора имеются продольные пазы, в которых располагаются проводники обмотки статора. Обмотка статора выполняется из медных обмоточных проводов круглого или прямоугольного сечения.

Требования к обмотке статора в основном сво­дятся к следующему: а) наименьший расход обмо­точной меди; б) удобство и минимальные затраты н изготовлении — технологичность; в) форма кривой ЭДС, наводимой в обмотке статора, должна был. практически синусоидальной.

Применительно к генераторам переменного тока это требование обусловлено тем, что при несинусоидальной ЭДС генератора в электрической цепи появляются высшие гармоники тока, оказывающие вредное влияние на работу всей энергосистемы: возрастают потери, возникают опасные перенапряжения, усиливается вредное влияние линий электропередачи на цепи связи. Применительно к двигателям переменного тока требование к синусоидальности ЭДС обмотки статора также весьма актуально, так как несинусоидальность ЭДС ведет к росту потерь и уменьшению полезной мощности двигателя.

Многофазная обмотка статора состоит из m₁ - фазных обмоток. Например, трехфазная обмотка (m₁ = 3) состоит из трех фазных обмоток, каждая из которых занимает Z₁\3 пазов, где Z₁ - общее число пазов сердечника статора. Каждая фазная обмотка представляет собой разом- кнутую систему проводников. Элементом обмотки является катушка, состоящая из одного

или нескольких витков. Элементы катушки, располагаемые в па­зах, называют пазовыми сторонами 1, а элементы, расположенные вне пазов и служащие для соединения пазовых сторон, называют лобовыми частями 2 (рис. 7.2). Часть дуги внутренней расточки статора, приходящаяся на один полюс, называется полюсным делением (м):

τ = πD₁ /(2р), (7.1)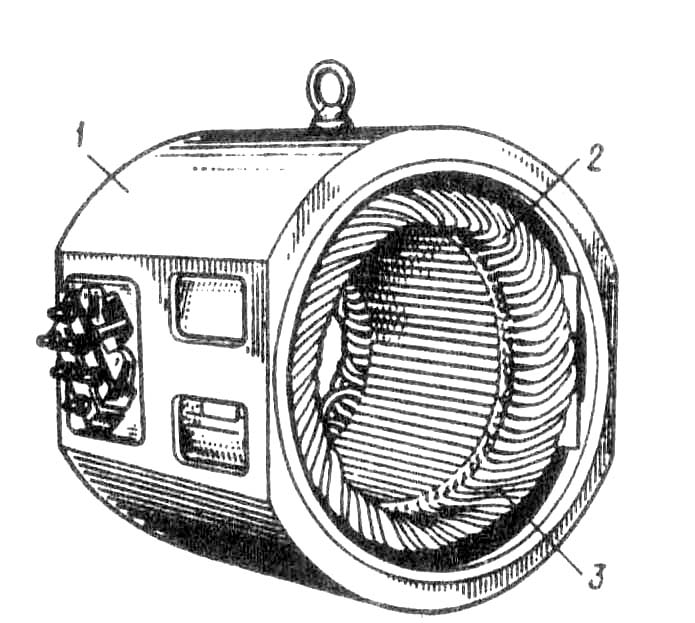

Рис. 7.1. Статор бесколлектор­ной машины переменного тока

где D₁ — внутренний диаметр статора, м; 2р — число полюсов.

Расстояние между пазовыми сторонами катушки, измеренное но внутренней поверхности стато­ра, называется шагом обмотки по пазам у₁. Шаг обмотки выражают в пазах. Шаг обмотки называется полным или диаметральным, если он равен полюсному делению:

y₁ = Z₁/(2p) =τ . (7.2)

В этом случае ЭДС витка определяется арифметической суммой ЭДС, наведенных в сторонах этого витка (рис. 7.3):

е = е₁ + е₂.

Если же шаг обмотки меньше полюсного деления (у₁ < τ), то он называется уко­роченным. У катушки с укоро­ченным шагом ЭДС меньше, чем у катушки с полным ша­гом.

Обмотка статора состоит, как правило, из большого чис­ла катушек, соединенных ме­жду собой определенным об­разом. Для удобного и наглядного изображения ка­тушек и их соединений поль­зуются развернутыми схема­ми обмоток. На такой схеме цилиндрическую поверхность статора вместе с обмоткой условно развертывают на плоскости, а все катушки

изображают одновитковыми в виде прямых линий.

Простейшая трехфазная обмотка статора двухполюсной машины состоит из трех катушек (А, В, С), оси которых смещены в пространстве относительно друг друга на 120 эл. град, т. е. на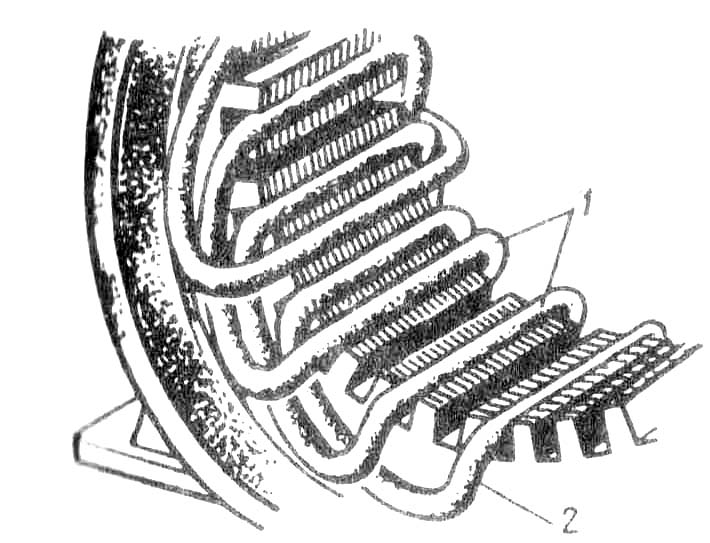

Рис 7.2. Расположение катушек в пазах сердечника статора

полюсного деления (рис. 7.4). Такая обмотка называется сосре­доточенной. Каждая катушка здесь представляет собой фазную обмотку.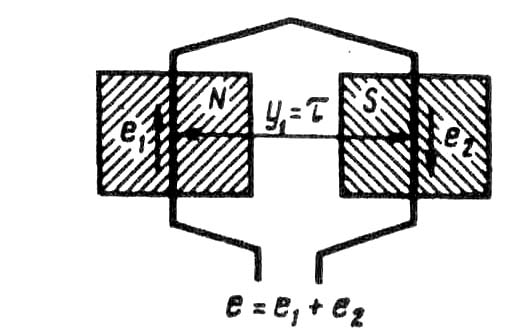

Рис. 7.3. При диамет­ральном шаге ЭДС в

пазовых сторонах ка­тушки направлены согласно

В соответствии с ГОСТом выводы трехфазных обмоток стато­ра обозначают следующим образом:
Первая фаза......начало С1 — конец С4

Вторая фаза..... » С2 — » С5

Третья фаза...... » СЗ — » С6

Конструкция обмотки статора в значи­тельной мере влияет на свойства машины переменного тока, в первую очередь на ее стоимость, КПД и рабочие характеристики.
§ 7.2. Электродвижущая сила катушки

Вращающееся магнитное поле, сце­пляясь с катушками обмотки статора, наводит в них ЭДС. Мгновенное значе­ние ЭДС (В) одной катушки с числом витков ω_k

e_k= B_δ2 l ν ω_k , (7.3)

где В_δ — магнитная индукция в воздушном зазоре между статором и ротором электрической машины, Тл;

ν = πD₁n₁ /60 = τ2рn₁ /60 = 2τ f₁ (7.4)

- линейная скорость движения магнитного поля относительно неподвижной катушки, м/с; πD₁ = τ 2р — длина поверхности рас­точки статора. С учетом (7.4) мгновенное значение ЭДС

катушки

e_k = В_δ 4τ l f₁ w_k (7.5)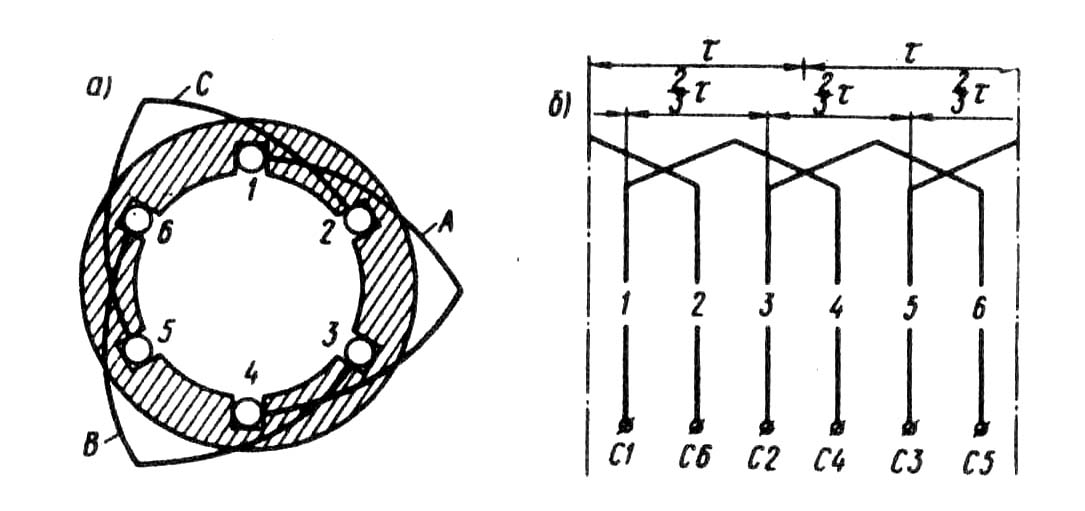


Рис. 7.4. Сосредоточенная трехфазная обмотка:

а — расположение катушек в пазах статора; б — развернутая схема обмотки
Как уже отмечалось, форма кривой ЭДС е_к зависит исключи­тельно от графика распределения индукции В_δ в воздушном зазо­ре. Однако даже при неравномерном зазоре (см. рис. 6.2) график индукции остается несинусоидальным. Поэтому ЭДС катушки е_к также несинусоидальна и наряду с первой (основной) синусои­дальной гармоникой ЭДС содержит ряд высших синусоидальных гармоник.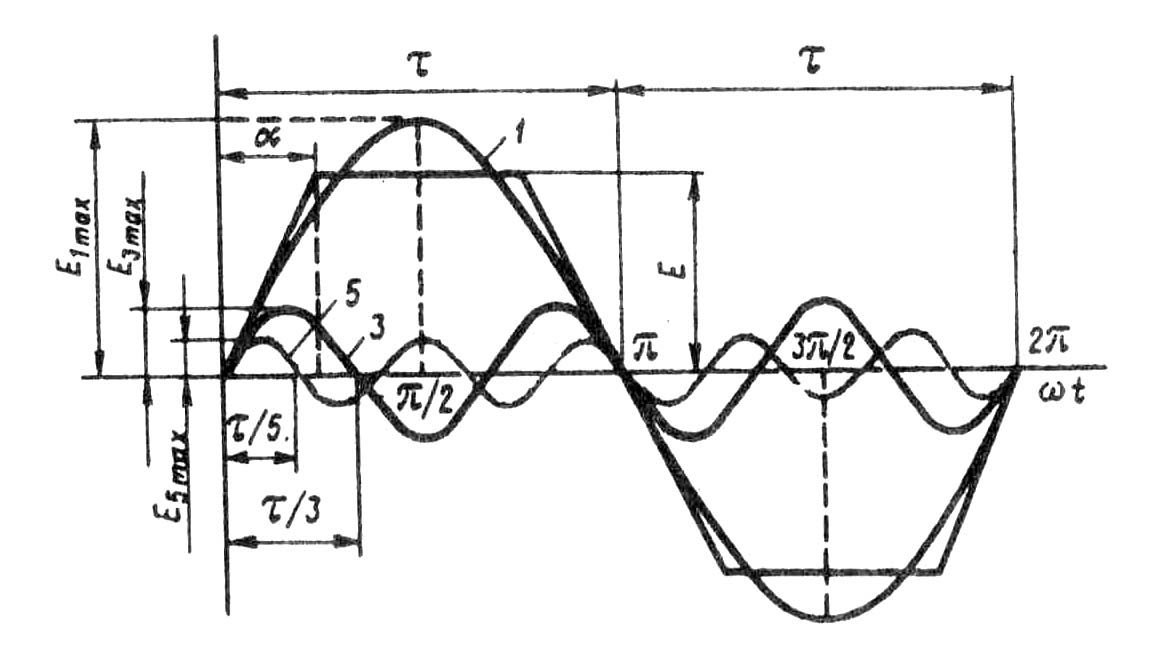

Рис. 7.5. Разложение трапецеидальной кривой ЭДС в гар­монический ряд

В связи с тем что кривая ЭДС симметрична относительно оси абсцисс, она содержит лишь нечетные гармоники (1, 3, 5 и т. д.). С некоторым приближением, приняв форму кривой ЭДС е трапецеидальной (рис. 7.5), можно записать следующее выражение гармо­нического ряда:

e = (sin sin ω₁t + ₂ sin 3 sin 3 ω₁t + ₂ sin 5 sin 5ω₁t + … + ₂ sin sin ω₁t), (7.6)

где — номер гармоники; ω₁, — угловая частота основной гармоники.

Из (7.6) видим, что с ростом номера гармоники ее амплитуда уменьшается пропорционально величине

sin / ² , а частота f = f₁ , т. е. растет пропорционально номеру гармоники. Поэтому прак-

тическое влияние на форму кривой ЭДС оказывают гармоники не выше седьмой. Таким, образом задача получения в обмотке статора синусоидальной ЭДС сводится к устранению или

мучительному ослаблению высших синусоидальных гармоник, в первую очередь третьей, пятой и седьмой.

Из § 1.10 известно, что токи и ЭДС третьей гармоники во всех фазах трехфазной обмотки совпадают во времени (по фазе). Поэтому в линейной ЭДС (напряжении) при схемах соединения об­моток звездой или треугольником третья гармоника отсутствует. Все, что касается третьей гармоники, распространяется и на выс­шие гармоники ЭДС, номера которых кратны трем (9, 15 и т. д.).

Рассмотрим вопрос о возможности устранения или значитель­ного ослабления гармоник выше третьей, главным образом пятой или седьмой. Допустим, что кривая распределения магнитной

и наряду с первой гармоникой В₁ содержит пятую В₅ (рис. 7.6, а). Если при этом об­мотка выполнена с диаметральным шагом (у₁ = τ ), то ЭДС первой и пятой гармоник (е₁ и е₅) в обеих сторонах катушки (витка) (рис 7.6, 6) складываются арифметически. В этом случае результирующая ЭДС катушки е_к.л, а следовательно, и ЭДС всей обмотки наряду с пер- вой содержат и пятую гармонику.

Если же шаг катушки укоротить на 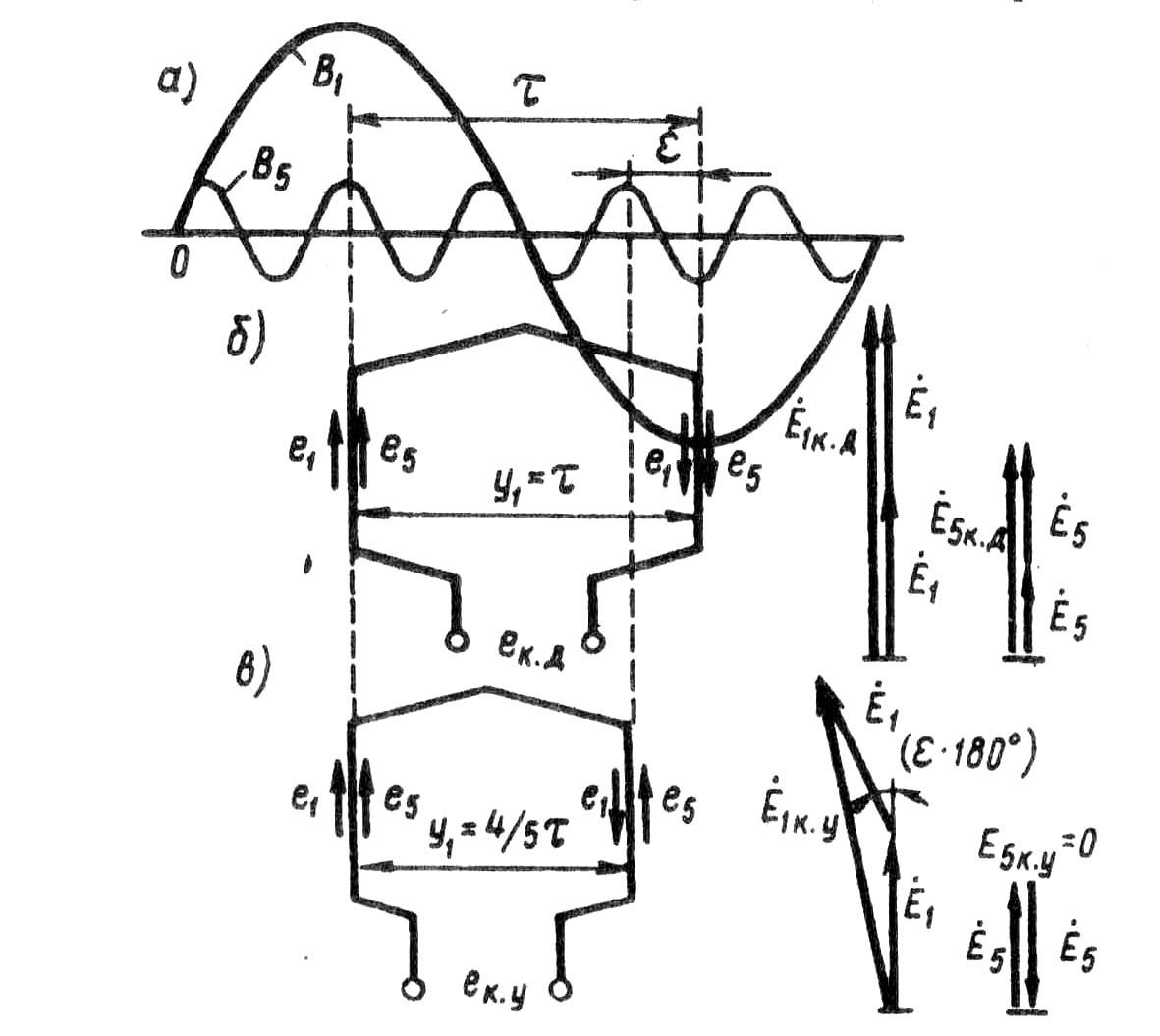полюсного деления, т. е. принять его равным

y₁ = ( )τ = 0,8τ,

Рис. 7.6. Укорочение шага обмотки на 1/5τ

то ЭДС пятой гармоники е₅, хотя и наводятся в пазовых сторонах катушки, будут находиться в противофазе относительно друг друга. В итоге сумма этих ЭДС в катушке будет равна нулю (рис. 7.6, в ) и ЭДС катушки будет содержать лишь первую (основную) ЭДС е₁ т. е. она станет практически синусоидальной. Аналогично, для уничтожения ЭДС седьмой гармоники тре­буется укорочение шага катушки на , полюсного деления τ, т. е. принимаем шаг катушки равным y₁ = ( )τ = 0,857τ.

Отношение шага у₁ к полюсному делению называют относи­тельным шагом обмотки = y₁/ τ Обычно относительный шаг принимают Р = 0,80 ÷ 0,89, что обеспечивает значительное ослабле­ние ЭДС высших гармоник.

Из построений, приведенных на рис. 7.6, видно, что уменьше­ние шага катушки на величину относительного укорочения ε = 1 - β вызывает ослабление не только ЭДС высших гармоник,

но и ЭДС первой (основной) гармоники. Объясняется это тем, что при диаметральном шаге (у₁ = τ) ЭДС первой гармоники Е_1к.д (рис. 7.6, б) равна арифметической сумме ЭДС, наводимых в пазовых сторонах катушки (Е_1к.д = 2Е₁), а при укорочении шага на величину ε (рис. 7.6, в) ЭДС в пазовых сторонах катушки оказываются сдви­нутыми по фазе относительно друг друга на угол ε·180° и ЭДС катушки Е_1к.у определяется геометрической суммой:

Е_1к.у = Е₁ + Е₁cos (ε·180°) < Е_1к.д. (7.7)

Уменьшение ЭДС катушки при укорочении ее шага на вели­чину ε = 1 - β учитывается коэффициентом укорочения шага k_y = Е_ку / Е_кд . Для первой гармоники

k_yl = sin(β· 90°). (7.8)

Для ЭДС любой гармоники

k_yυ = sin(υβ · 90°). (7.9)

Ниже приведены значения коэффициентов укорочения k_yυ в зависимости от относительного шага β обмотки для различных гармоник ЭДС:

Относительный шаг..............	4/5	6/7	1
Коэффициент укорочения kyυ: 1-я гармоника............... 5-я » ............... 7-я » ...............	0,951 0,000 0,573	0,975 0,433 0,000	1,000 1,000 1,000

В заключение следует отметить, что укорочение шага обмотки по пазам возможно лишь в двухслойных обмотках (см. § 7.1). Однослойные обмотки выполняются с диаметральным ша- гом, поэтому ЭДС, наводимые в них, содержат в значительной мере высшие гармоники 5-го и

7-го порядка. Это ограничивает применение однослойных обмоток в асинхронных двигателях мощностью более 15 - 22 кВт.
§ 7.3. Электродвижущая сила катушечной группы

Обмотки статора разделяются на сосредоточенные и распре­деленные. При сосредоточенной обмотке все катушки одной фа­зы, приходящиеся на полюс и образующие катушечную группу, укладываются в двух пазах, т. е. сосредоточиваются вместе и об­разуют одну большую катушку. Примером такой обмотки может служить трехфазная обмотка, представленная на рис. 7.4. По ряду причин сосредоточенные обмотки не получили распространения. Одна из причин — необходимость вырубки в пластинах статора пазов большой площади, необходимой для размещения значитель­ного числа пазовых сторон. Это ведет к необходимости увеличе­ния наружного диаметра статора, а следовательно, к увеличению размеров машины.

В распределенных обмотках все катушки равномерно рас­положены по периметру расточки статора. При этом катушки каждой фазы, приходящиеся на полюс, т. е. катушки каждой катушечной группы, занимают более двух пазов, например че­тыре, шесть и т. д.

Весьма важным параметром обмотки статора является число пазов, приходящихся на полюс

q₁ =Z₁/(2pm₁), (7.10)

где m₁ — число фаз в обмотке (для трехфазной обмотки m₁ = 3).

В сосредоточенной обмотке, где на пару полюсов приходится два паза каждой фазы, а всего пазов Z₁ = 2pm₁, число пазов на по­люс и фазу q =1. В распределенной обмотке q > 1. В распреде­ленной двухслойной обмотке статора число катушечных групп в каждой фазе равно числу полюсов 2р, а общее число катушечных групп трехфазной обмотки А = 2pm_l. При этом число катушек в катушечной группе равно q₁. Однако сосредоточенные и распре­деленные обмотки различаются не только конструкцией. Имеется также разница и в величине и форме графиков ЭДС, наведенных в сосредоточенной и распределенной обмотках. Для разъяснения обратимся к рис. 7.7, где показаны две одновитковые катушки фазной обмотки, сосредоточенные в двух пазах (а), и такие же две катушки, образующие катушечную группу и сосредоточенные в четырех пазах (б).

В случае сосредоточенной обмотки (рис. 7.7, а) ЭДС, наведенные в двух катушках, совпадают по фазе; в этом случае ЭДС катушечной группы £_r.с равна арифметической сумме ЭДС катушек:

Е_r.c = Е_к1 + Е_к2. (7.11)

В случае распределенной обмотки обе катушки сдвину­ты в пространстве относительно друг друга на пазовый угол γ. По­этому ЭДС, наводимые в катушках катушечной группы, оказались сдвинутыми по фазе относительно друг друга на угол γ (рис. 7.7, б). Исходя из этого ЭДС катушечной группы распределенной обмот­ки Е_г.р равна геометрической сумме ЭДС катушек, число которых равно q₁ :

_г.р =

Как видно из приведенных на рис. 7.7 векторных диаграмм, ЭДС катушечной группы сосредоточенной обмотки Е_rс больше, чем ЭДС при распределенной обмотке Е_гр. Уменьшение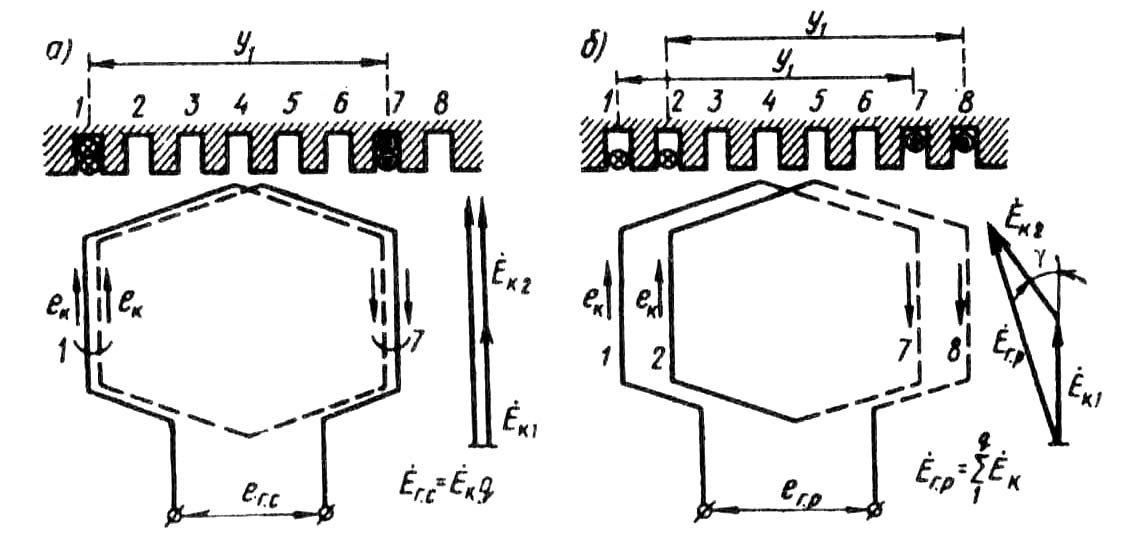

Рис. 7.7. К понятию о коэффициенте распределения

ЭДС катушечной группы при переходе от сосредоточенной обмотки к распределенной

распространяется на ЭДС не только первой, но и высших гармоник. Для количественной оценки этого уменьшения ЭДC пользуются коэффициентом распределения обмотки, представляющим собой отношение ЭДС:

k_p = (E_г.р/E_г.с) < 1.

Коэффициент распределения обмотки для первой гармоники
k_p = (7.12)

где γ - угол сдвига по фазе между векторами пазовых ЭДС, т. е. ЭДС, наводимых в проводниках, лежащих в соседних пазах статора, эл. град:

γ = 360p/Z₁. (7.13)

Так как угол сдвига по фазе между векторами пазовых ЭДС для ν-й гармоники в ν раз больше пазового угла γ, то коэффициент распределения обмотки для любой гармоники ЭДС равен

k_pv = (7.14)

Ниже приведены значения коэффициента распределения для первой, третьей, пятой и седьмой гармоник ЭДС:

Число пазов на полюс и фазу q1…	1	2	3	4	5	6	∞
Коэффициент распределения kp 1-я гармоника 3-я » ............. 5-я » ............. 7-я » .............	1,000 1,000 1,000 -1,000	0,966 0,707 0,259 -0,259	0,960 0,667 0,217 -0,178	0,958 0,654 0,204 -0,157	0,957 0,646 0,200 -0,149	0,956 0,644 0,197 -0,145	0,955 0,636 0,191 -0,136

Из приведенных данных видно, что увеличение q₁ вызывает сравнительно небольшое уменьшение коэффициента распределе­ния для основной гармоники и значительное уменьшение его для высших гармоник.
§ 7.4. Электродвижущая сила обмотки статора

Мгновенное значение ЭДС катушки статора по (7.5)

e_k = B_δ 4 τ l f₁ ω_k.

Eсли принять закон распределения магнитной индукции в воздушном зазоре синусоидальным (B_δ = B_max sin ω₁ t), то макси­мальное значение ЭДС катушки

E_kmax = B_max4 τ l f₁ω_k (7.15)

При синусоидальном законе распределения среднее значение магнитной индукции

В_ср = (2/π)B_max, откуда

B_max =(2/π)B_ср (7.16)

Тогда с учетом (7.15) и (7.16) получим

E_kmax= 2πВ_срτ lf₁ ω_k (7.17)

Переходя к действующему значению ЭДС, получим

E_k = E_kmax/ = (2π / ) B_срτlf₁ω_k(7.18)

Произведение полюсного деления т на длину l представляет собой площадь полюсного деления, т. е. площадь магнитного по­тока одного полюса. Тогда произведение B_ср τ l = Ф , т. е. равно ос­новному магнитному потоку статора. Учитывая это, а также то, что 2π / = 4,44 , получим выражение действующего значения ЭДС катушки с диаметральным шагом (у₁ = τ ):

E_к = 4,44Фf₁ω_k(7.19)

Для определения ЭДС обмотки фазы статора необходимо ЭДC катушки Е_к умножить на число последовательно соединенных катушек в фазной обмотке статора. Так как число катушек в кату­шечной группе равно q₁, а число катушечных групп в фазной об­мотке равно 2р, то фазная обмотка статора содержит 2pq₁ катушек.

Имея в виду, что число последовательно соединенных витков в фазной обмотке ω₁ = 2p q₁ ω_к , получим ЭДС фазной обмотки ста­тора (В):

Е₁ = 4,44 Ф f₁k_об1. (7.20)

В этом выражении k_об1 — обмоточный коэффициент для ос­новной гармоники, учитывающий уменьшение ЭДС основной гармоники, наведенной в обмотке статора, обусловленное укоро­чением шага обмотки и ее распределением. Значение обмоточного коэффициента определяется произведением коэффициента укоро­чения k_у1 и распределения k_р1 :

k_об1 = k_у1k_р1. (7.21)

Для обмоток с диаметральным шагом k_об1 = k_р1

Выражение (7.20) определяет значение фазной ЭДС об­мотки статора. Что же касается линейной ЭДС, то ее значение зависит от схемы соединения обмотки статора: при соединении

звездой Е_1л = Е₁, а при соединении треугольником Е_1л = E₁ .
Пример 7.1. Статор трехфазного асинхронного двигателя (см. рис. 7.1) внутренним диаметром

D₁ = 435 мм, длиной l = 270 мм имеет число пазов Z₁ = 60. Шаг обмотки статора по пазам

y₁ = 12, число витков в катушке обмотки статора ω_k = 2. Определить ЭДС одной фазы обмотки

если магнитная индукция в воздушном зазоре B_δ = 0,75 Тл, а частота переменного тока f₁ = 50 Гц; 2р = 4.
Решение. 1. Полюсное деление

τ = πD₁/ (2p) = π 435/ 4 = 341 мм,

или в зубцовых делениях τ = Z₁/(2p) = 60/4 = 15 .

2. Относительный шаг обмотки

β = y₁/τ = 12/15 = 0,80.

3. Коэффициент укорочения шага обмотки по (7.8)

k_yl = sin(β· 90) = sin(0,80-90°) = 0,951 .

4. Число пазов на полюс и фазу по (7.10)

q₁ = Z₁ / (2pm₁) = 60 / (4·3) = 5

5. Пазовый угол по (7.13)

γ = З60р /Z₁ = 360 • 2/60 = 12 эл. град.

6. Коэффициент распределения обмотки по (7.12)

k_p1 = = = 0,957

7. Обмоточный коэффициент по (7.21)

k_об1= k_y1 k_p1= 0,951 · 0,957 = 0,91.

8. Основной магнитный поток

Ф = (2/π)В_δ l₁ τ 10^-6 = (2/π) 0,75 · 270 · 341· 10^-6 =0,044 Вб.

9. Число последовательно соединенных витков в обмотке фазы

ω₁ = 2p q₁ ω_k =4·5·2 = 40.

10. ЭДС обмотки фазы статора по (7.20)

E₁ = 4,44 Ф f₁ и ω₁ k_о61 = 4,44 • 0,044 • 50 • 40 • 0,91 = 357 В.

Значение линейной ЭДС этой обмотки зависит от схемы ее соединения: при соединении звездой Е_л = Е₁ = • 357 = 618 В, а при соединении треугольни­ком Е_л = Е₁ = 357 В.
§ 7.5. Зубцовые гармоники ЭДС

Наличие зубцов и пазов на по­верхности статора создает неравно­мерность воздушного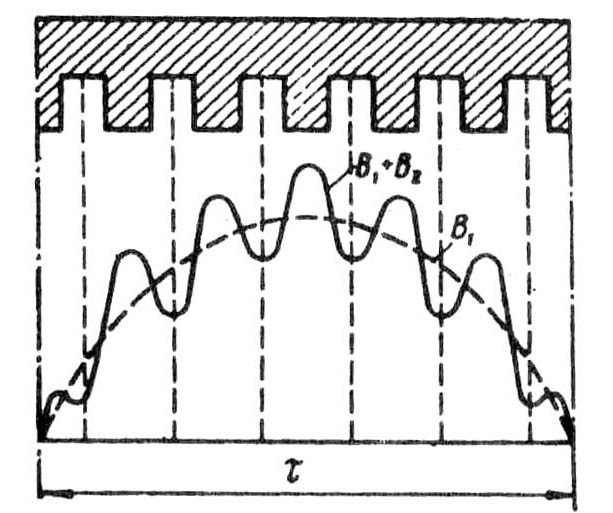


Рис. 7.8 График магнитной индукции основной гармоники В₁,

искаженной зубцовой гармоникой В_z
зазора. По этой причине все гармонические составляющие магнитного поля, обусловленные несинусоидально­стью кривой магнитной индукции (см. рис. 6.2), приобретают зубча­тую форму. Каждая из этих иска­женных гармоник индуцирует в обмотке статора две ЭДС: собст­венной частоты f_v и зубцовую.

Практическое влияние на работу машины может оказать зубцовая ЭДС поля основной

гармоники (рис. 7.8). Мгновенное значение этой ЭДС

e_z = E_zmaxsinω₁tcos 2Qω₁t (7.22)

или, учитывая, что sin ω₁ t cos 2Q ω₁ t = 0,5sin(ω₁ t + 2Q ω₁ t) + 0,5sin(ω₁ t -2Q ω₁ t), получим

e_z = 0,5 E_zmax [sin(2Q+1) ω₁ t – sin (2Q - 1)ω₁ t], (7.23)

где Q = Z₁ /(2p) — число пазов на полюс.

Из (7.23) следует, что зубцовая ЭДС от основной гармони­ки поля может быть разложена на две составляющие с одинаковыми амплитудными значениями, но разными час­тотами:

f_z^/ = (2Q+1)f₁ (7.24)

f _z^//= (2Q-1)f₁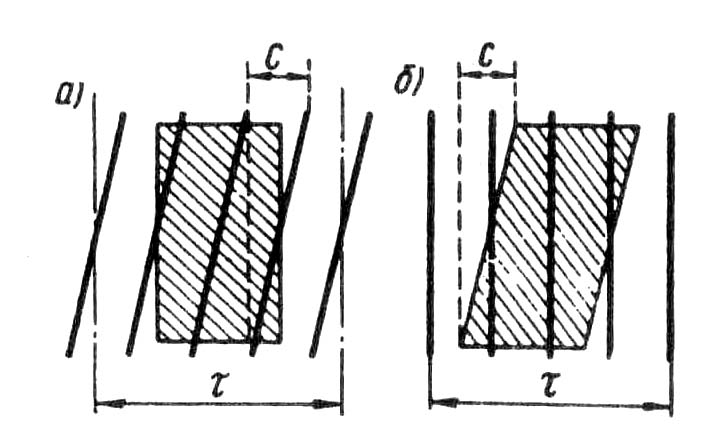

Рис. 7.9. Скос пазов (а) и скос полюсного наконечника (б)
Например, при 2р = 4, Z₁ = 24 и f₁ = 50 Гц основная гар­моника поля вызывает зубцовые ЭДС, частота которых:

f_z^/ = (2 • 6 + 1)50 = 650 Гц (13-я гармоника);

f'_z^// = (2 • 6 - 1)50 = 550 Гц (11 -я гармоника).

Вредное действие зубцовых гармоник ЭДС выражается в том, что они вызывают дополнительные потери в машине и, имея по­вышенную частоту, оказывают мешающее влияние на линии связи.

Так как сокращение шага обмотки по пазам у₁ всегда кратно числу зубцов, то оно не позволяет уменьшить зубцовые гармоники ЭДС. Эффективное средство ослабления зубцовых гармоник ЭДС - скос пазов или скос полюсных наконечников (в синхронных машинах). Обычно этот скос составляет одно зубцовое деление (рис. 7.9). При скосе пазов или полюсных наконечников ЭДС, ин­дуцируемые в ряде последовательных точек по длине проводника, будут сдвинутыми по фазе относительно друг друга. Это ведет к уменьшению ЭДС проводника, учитываемой коэффициентом ско­са пазов

k_ck =

где τ и с — в зубцовых делениях.

При скосе пазов на одно зубцовое деление t₁ для первой гар­моники коэффициент k_CKl ≈ 1 , а для гармоник зубцового порядка k_ckv << 1. Например, при 2р = 4, Z₁ = 48 и скосе пазов на одно зуб­цовое деление (с = 1) для основной гармоники (v = 1) коэффициент скоса пазов

k_CKl = 0,995 , для зубцовой гармоники (v = 13) коэффициент k_скl3 = 0,590 .
Контрольные вопросы

1. Что такое шаг обмотки по пазам и какой должна быть его величина?

2. На какие гармонические составляющие можно разложить несинусоидальную кривую ЭДС,

наведенной в обмотке статора?

3. Какие применяются средства подавления высших гармоник ЭДС в обмотке статора?

4. Каким образом можно ослабить зубцовые гармоники ЭДС в обмотке статора?

ГЛАВА 8

• Основные типы обмоток статора
§ 8.1. Трехфазные двухслойные обмотки с целым числом пазов на полюс и фазу
Обмотки статора машин переменного тока по своей конструкции разделяются на двух- и одно­слойные. В двухслойной обмотке пазовая сторона катушки занимает половину паза по его высоте, а другую половину этого паза занимает пазовая сто­рона другой катушки (рис. 8.1, а). В однослойной обмотке статора пазовая сторона любой катушки занимает весь паз (рис. 8.1, б).

Рассмотрим принцип выполнения трехфазной двухслойной обмотки с целым числом пазов на по­люс и фазу q₁ равным 2; 3; 4 и т. д. В этом случае обмотка каждой фазы занимает q₁ пазов в пределах каждого полюсного деления. Таким образом, для образования трехфазной обмотки зубцовый слой сердечника статора в пределах каждого полюсного деления следует разделить на три зоны по q₁ пазов в каждой зоне.

Рассмотрим порядок построения развернутой схемы трехфазной двухслойной обмотки статора на примере обмотки, имеющей следующие данные: число фаз m₁ = 3, число полюсов 2р = 2, число пазов в сердечнике статора Z₁ = 12, шаг обмотки по пазам диаметральный, т. е. y₁ = τ.

Шаг обмотки y₁ = Z₁ / (2p) = 12/2 = 6 пазов; число пазов на полюс и фазу q₁ = Z₁/ (m₁ 2p) = =12/ (3 2) = 2 паза; пазовый угол γ =360p/ Z_l =360 1/12 = 30 эл. град. Угол сдвига между осями фазных обмоток составляет 120 эл. град, поэтому сдвиг между на­чалами фазных обмоток А, В и С, выраженный в пазах, λ = 120/γ = 120/30 = 4 паза.

На развернутой поверхности статора размечаем пазы (Z₁ = 12) и полюсные деления (2р = 2), а затем размечаем зоны по q₁ = 2 паза для всех фаз (рис. 8.2, а); при этом расстояние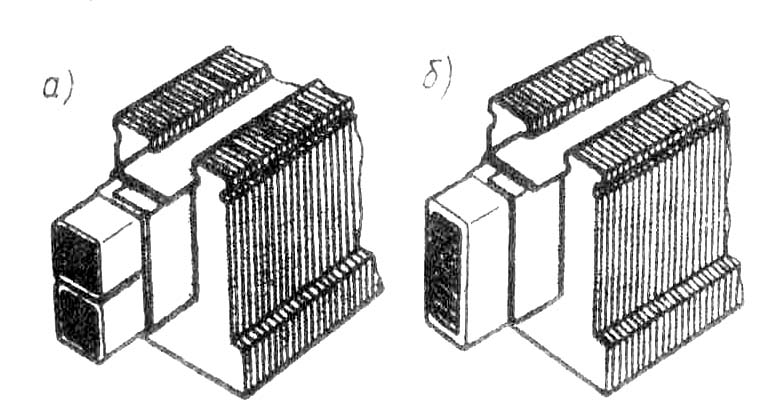


Рис. 8.1. Расположение пазовых сторон двухслойной (а)

и однослойной (б) об­моток статора
между зоной какой-либо фазы в одном полюсном делении и зоной этой же фазы в другом полюсном делении должно быть рав­но шагу обмотки у₁= 6 пазов.

Далее отмечаем расстояние между началами фазных обмоток λ = 4 паза. Изображаем на схеме (рис. 8.2, 5) верхние (сплошные линии) и нижние (пунктирные линии) пазовые стороны катушек фазы А (катушки 1,2, 7 и 8). Верхнюю сторону катушки 1 (паз 1) лобовой частью соединяем с нижней стороной этой же катушки (паз 7), которую, в свою очередь, присоединяем к верхней стороне катушки 2 (паз 2). Верхнюю сторону катушки 2 (рис. 8.2, б) также лобовой частью соединяем с нижней стороной этой же катушки (паз 8) и получаем первую катушечную груп­пу обмотки фазы А (H1А— K1А).

Аналогично получаем вторую катушечную груп­пу фазы А, состоящую из последовательно соеди­ненных катушек 7 и 8 (Н2А— К2А). Катушечные группы соединяем последовательно

встречно, для чего К1А присоединяем к К2А. Присоединив начало первой катушечной группы H1А к выводу обмотки С1, а начало второй катушечной группы Н2А — к выводу С4, получаем фазную обмотку А.

Приступаем к соединению пазовых сторон катушек фазы В: к .пушек 5 я 6 (первая катушеч- ная группа) и катушек 11 и 12 (вто­рая катушечная группа). Проделав то же самое с катушками фаз­ной обмотки С и соединив катушечные группы этих фазных обмоток, так же как это было сделано в фазной обмотке А, получим фазные обмотки фазы В (С2—С5) и фазы С (СЗ—С6). В окончательном виде развернутая схема трехфазной обмотки представле­на на рис. 8.2, в.

Двухслойные обмотки в электрических машинах переменного тока получили наибольшее

распространение. Это объясняется рядом их достоинств, из которых главным является возможность любого укорочения шага обмотки, что дает, в свою очередь, возжность максимально приблизить форму кривой ЭДС к синусоиде(см. § 7.3). Однако двухслойные обмотки не

лишены недостатков— это затруднения в применении станочной укладки обмотки, а также

трудность ремонта обмотки при повреждении изоляции пазовых проводников нижнего слоя.

Катушечной группой называют ряд последовательно соединенных между собой катушек, которые лежат в соседних пазах и принадлежат одной фазной обмотке. Каждая катушечная

группа имеет q₁ последовательно соединенных катушек. Колиичество катушечных групп в

фазной обмотке равно числу полюсов. Общее количество катушечных групп в двухслойной

обмотке равно 2рm₁.

Катушечные группы каждой фазы обмотки статора могут, быть соединены последовательно

или параллельно, что влияет на число параллельных ветвей в обмотке.

На рис. 8.2, б показано последовательное соединение двух ка­тушечных групп фазной обмотки, для чего необходимо нижний конец первой катушечной группы (К1А) соединить с нижним кон­цом второй катушечной группы (К2А), а верхние концы вывести к зажимам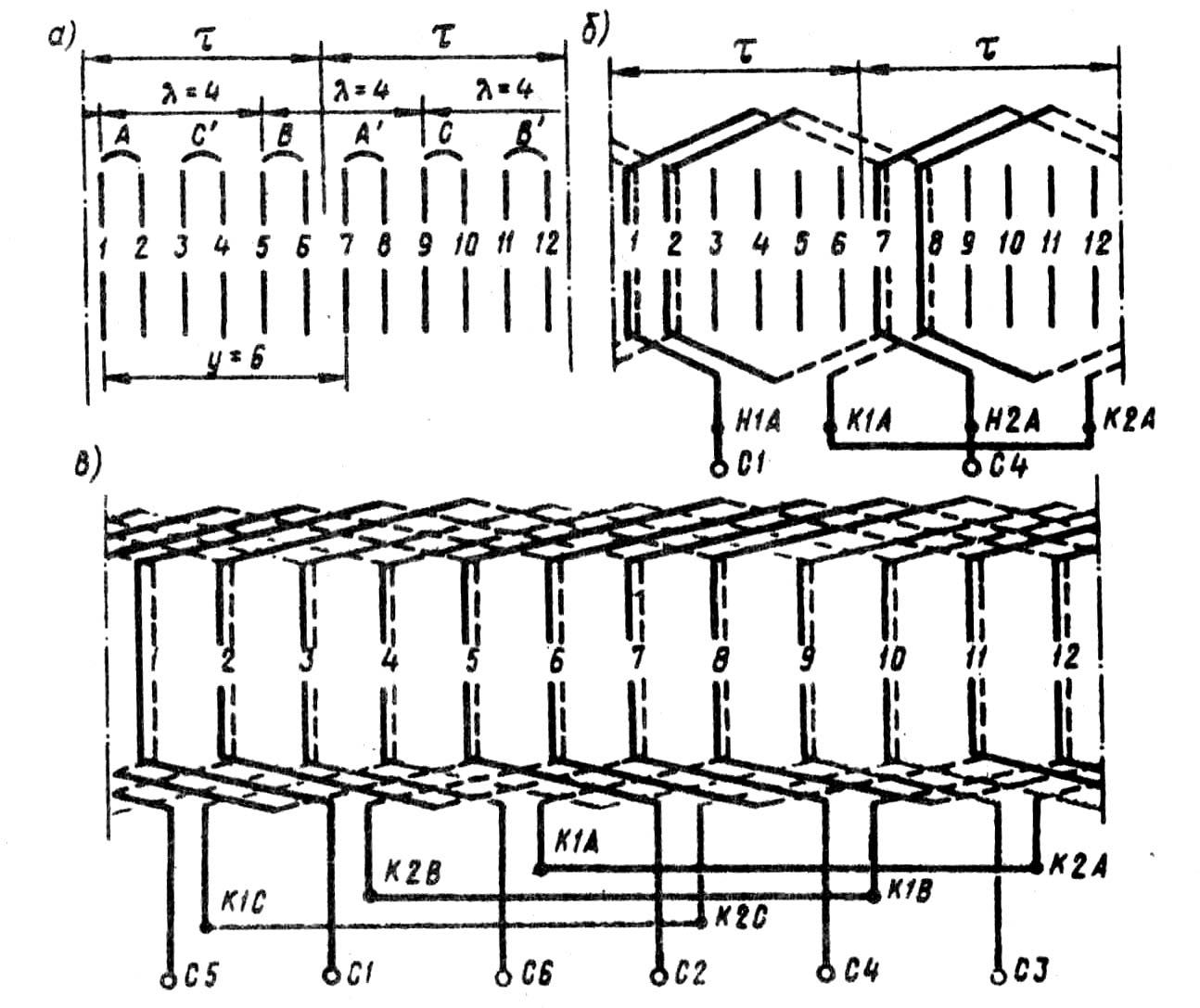

Рис. 8.2. Порядок построения развернутой схемы трехфазной

двухслойной обмотки статора: Z₁ = 12, 2р = 2, у₁ = 6, q₁ = 2
фазной обмотки (С1—С4). При таком соединении кату­шечных групп ЭДС фазной обмотки представляет собой сумму ЭДС всех катушечных групп.

На рис. 8.3, а показано последовательное соединение четырех катушечных групп. Первая и вторая группы соединены нижними концами, вторая и третья группы соединены верхними концами, третья и четвертая — нижними, а к выводам фазной обмотки при­соединены верхние концы первой и четвертой катушечных групп. При последовательном соединении катушечных групп каждая фазная обмотка независимо от числа полюсов машины содержит одну параллельную ветвь (a₁ = 1). Двухслойная обмотка в каждой фазе имеет 2р катушечных групп, поэтому, соединив все группы параллельно, получим обмотку, состоящую из 2р параллельных ветвей (а₁ = 2р).

На рис. 8.3, б показано параллельное соединение четырех катушечных групп: к одному выводу обмотки (С1) подключены верхние концы нечетных групп (I и III) и нижние концы четных групп (II и IV), оставшиеся концы катушечных групп присоедине­ны к другому выводу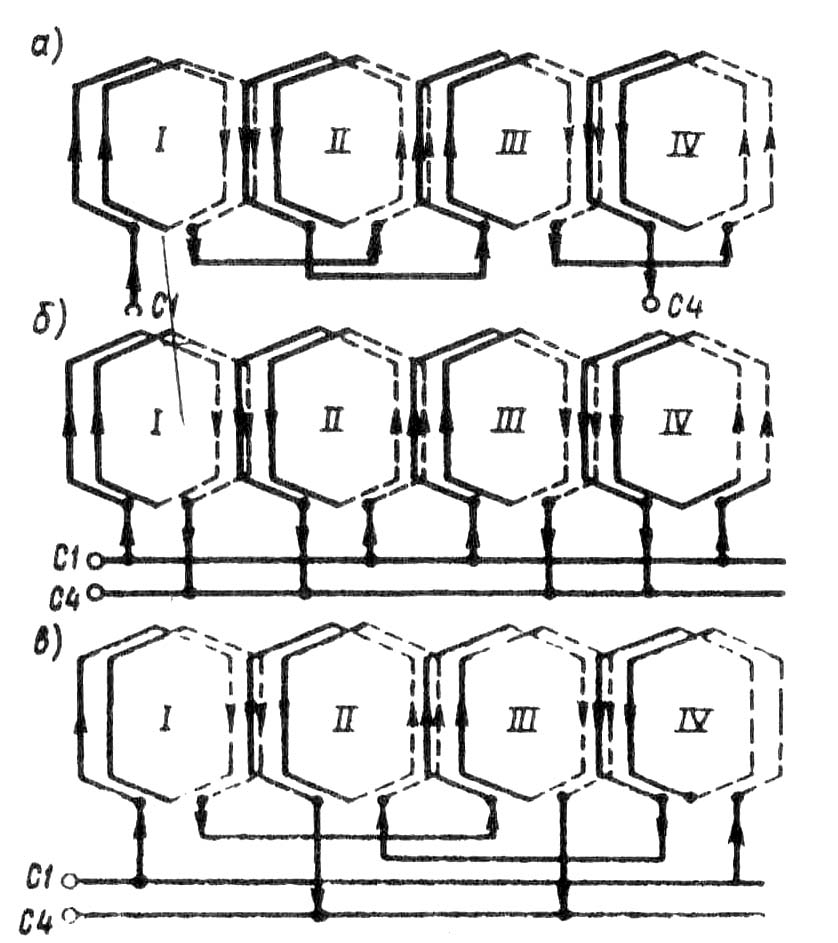

Рис. 8.3 Способы соединения катушечных групп

фазной обмотки (С4). Такой порядок при­соединения групп объясняется следующим: ЭДС рядом лежащих катушечных групп одной фазной обмотки сдвинуты по фазе друг относительно друга на 180°, так как эти кату­шечные группы распо­ложены под разноимен­ными полюсами. Поэтому, чтобы ЭДС радом лежащих катушечных групп фазной обмотки совпали по фазе, приходится их присоединять меняя концы.