СМО. Однородная
 Скачать 14.18 Kb. Скачать 14.18 Kb.
|
|
Исходная СМО определяется как одноканальная (1 служащий отдела). Из условия – входящий поток бесконечный, образуется очередь неограниченной длины. Система однородная fλ(t)=λe-λt fμ(t)=μe-μt Условие стационарного режима: 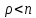 n – число каналов При n=1 и n=2 условие стационарного режима не достигается, очередь бесконечна. Рассмотрим n=3 (без образования бесконечно длинных очередей): Вероятность 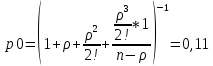 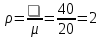 Длина очереди: 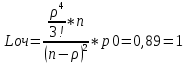 В среднем очередь состоит из 1 механика. Отсюда потери рабочего времени механика Пм=600*1=600 руб в час. Рассмотрим n=4 (без образования бесконечно длинных очередей): Вероятность 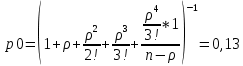 Длина очереди: 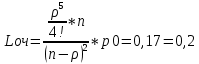 В среднем очередь состоит из 0,2 механика. Тогда затраты на одного механика в очереди: Зм = 0,2*600=30 руб в час. Затраты на ввод дополнительного сотрудника обслуживния: Зсо = 350 руб в час. Изменение затрат при введении 4го сотрудника обслуживание: З=Пм-Зм-Зсо=600-30-350=220 руб в час. Изменение затрат носит положительный характер, что говорит об их сокращении. Рассмотрим n=5 (без образования бесконечно длинных очередей): 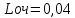 Зм=0,04*600=24 Зсо=350 Изменение затрат при введении 5го сотрудника обслуживание: З=Пм-2*350-24=.-124 Носит отрицательный характер, что говорит о том, что оптимальной является СМО с 4 сотрудниками обслуживания. |
