Исследовательская работа Контактное число. Контактное число. Ое образовательное учреждение Лицей 82 Сормовского района г. Н. Новгорода Контактное число Кузнецов Семён
 Скачать 0.72 Mb. Скачать 0.72 Mb.
|
|
Научное общество учащихся «Эврика» Муниципальное автономное образовательное учреждение «Лицей №82» Сормовского района г.Н.Новгорода Контактное число Выполнил: Кузнецов Семён ученик 9 б класса Научный руководитель Зотова В.И., учитель математики Н. Новгород 2022 Содержание Стр. Введение..…………………………………………………………………………….3 1.Задачи через измерения…...………………………………………………………4 2.Первое измерение………………………………………………………………….5 3.Второе измерение………………………………………………………………….6 4.Третье измерение…………………………………………………………………..7 5.Проблема восприятия и визуализации.…………………………………………..8 6.Многомерное пространство………………………………………………………9 Заключение………………………………………………………………………….11 Список литературы…………………………………………………………………13 Введение В настоящее время в геометрии существует большое количество нерешённых задач. Часть из них связана с многомерными пространствами размерностью n>3. Данные проблемы на данный момент являются нерешёнными для всех n, однако для некоторых есть точные решения. Эти задачи актуальны, ведь с появлением компьютеров и их вычислительных возможностей, гораздо проще описывать то, что почти невозможно визуализировать без искажений. Задача рассмотренная в данной работе имеет практическое применение в теории кодирования. В 1948 году Клод Шэннон опубликовал работу по теории информации, показывающую возможность передачи данных без ошибок в зашумленных каналах связи используя координаты упаковки единичных сфер в n-мерном пространстве 1.Задачи через измерения В вершинах гиперкуба с ребром 2 и центром в начале координат расположены гиперсферы радиуса 1. Гиперсфера радиуса r с центром в начале координат касается каждой из ранее заданных гиперсфер. Чему равно r? Чему равно контактное число в евклидовых пространствах с размерностью n? (далее K(n)) Определения: Гиперсфера – обобщение сферы на произвольное количество измерений. Теорема: 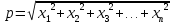 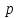 = = 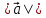 = = 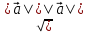 = =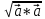 = =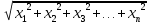 Гиперкуб – обобщение куба на произвольное количество измерений. 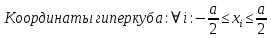 Контактное число – максимальное количество шаров единичного радиуса, которые могут одновременно касаться одного такого же шара. 2.Первое измерение 2.1 Отметим, что окружность в центре выродится до точки, откуда r = 0  2.2 Очевидно, что для задачи ответ 2 с таким рисунком. K(1) = 2  3. Второе измерение 3.1 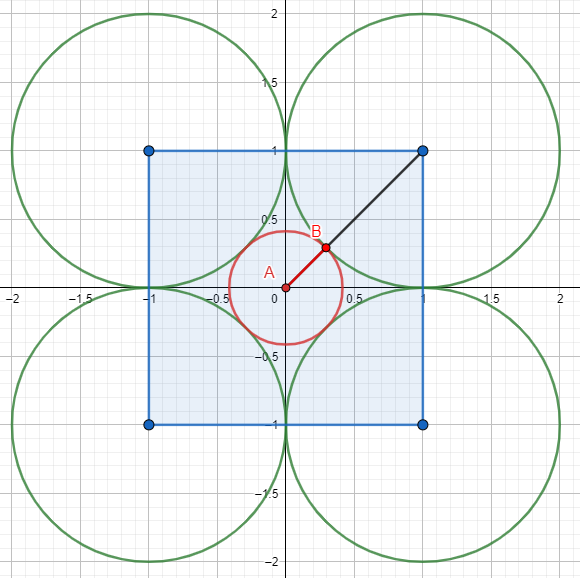 Очевидно, что r = AB = 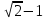 3.2 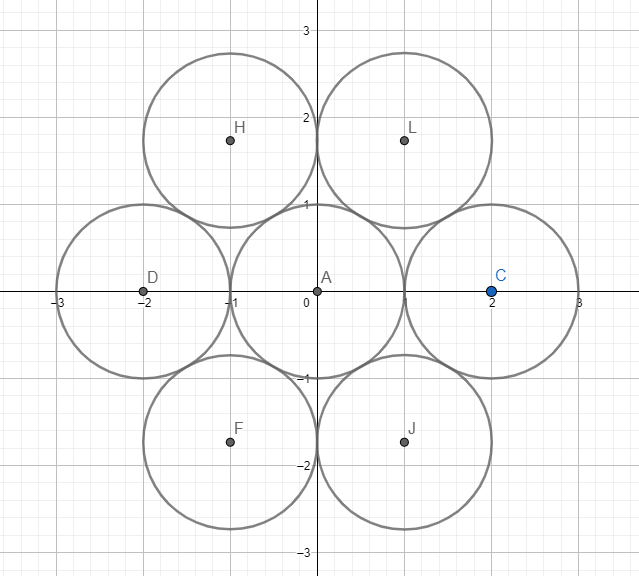 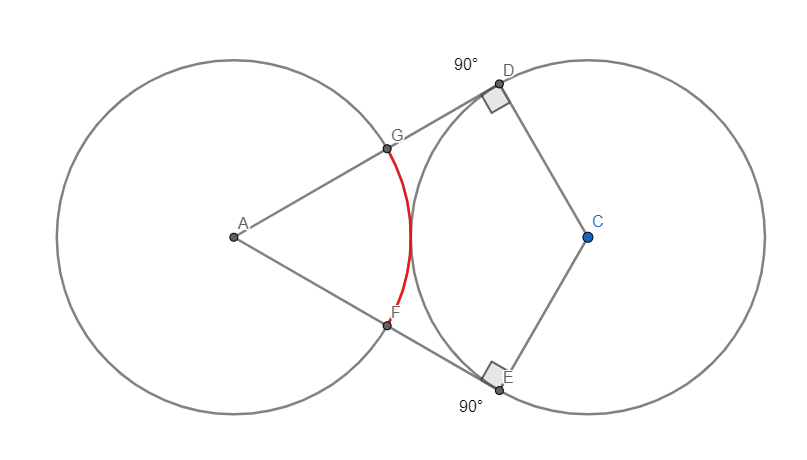 Координаты точек окружностей: (2;0);(1; 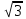 );(-1; );(-1;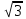 );(-2;0);(-1; );(-2;0);(-1;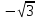 );(1; );(1;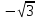 ) )Исходя из данного построения, мы можем сказать, что K(2) ≥ 6. Но также если мы спроецируем единичную окружность на такую же окружность, то проекция отсечёт дугу в 60°. А значит максимум около круга можно описать 360° / 60° = 6 Откуда 6 ≤ K(2) ≤ 6 => K(2) = 6 4.Третье измерение 4.1 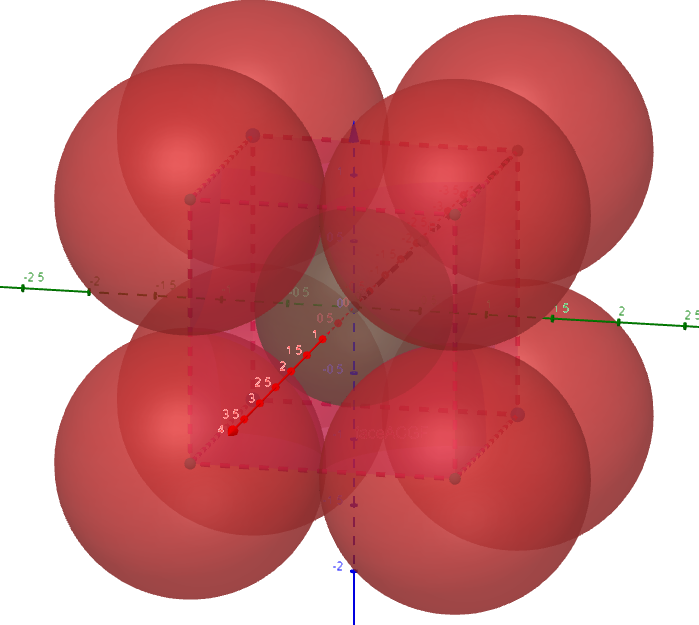 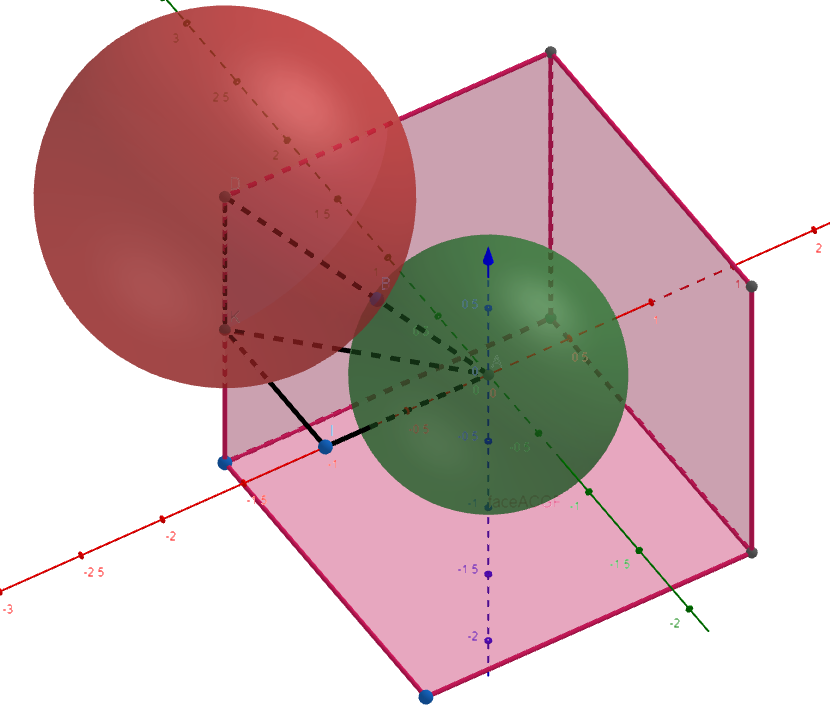 Пренебрежём неважными для нас деталями и будем пользоваться второй картинкой. Из неё и формулы для расстояния до точки можем понять, что радиус центральной сферы: 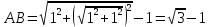 4.2 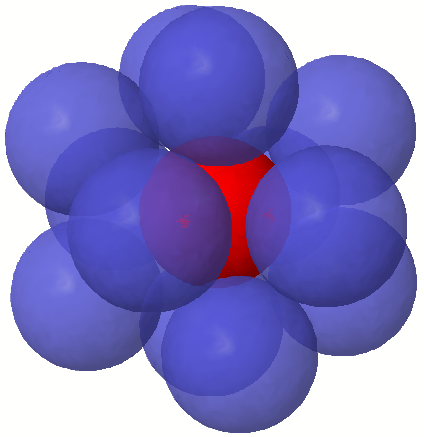 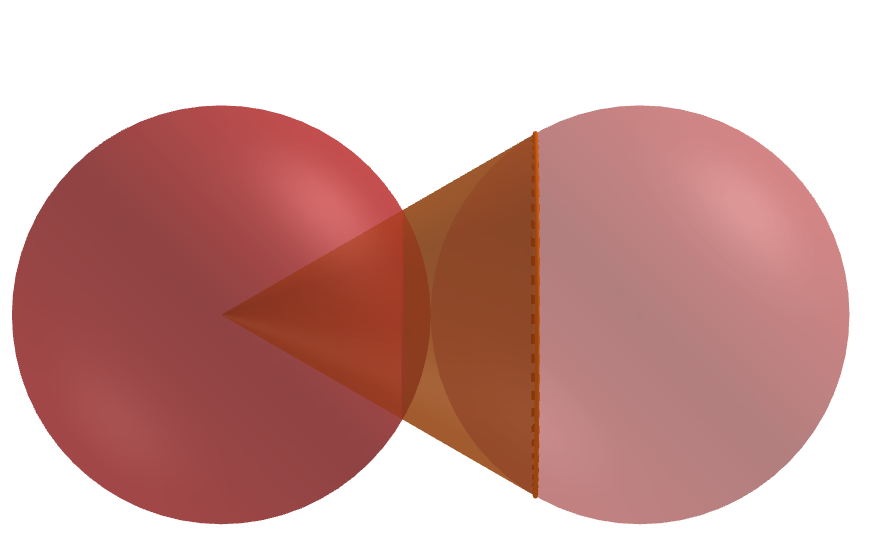 В приложении есть программа показывающая построение для вершин 12 шаров, а также высчитывающий расстояние между вершинами => К(3) ≥ 12 При проецировании же можно получить, что проекции занимает 2π(1-cos( 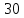 °)), что будет составлять °)), что будет составлять 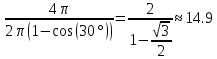 => 12 ≤ K(3) ≤ 14 => 12 ≤ K(3) ≤ 14Доказательство невозможности K(3) = 14, есть в приложении, когда доказательство что K(3) ≠ 13 было опубликовано в 1953 году => K(3) = 12 5.Проблема восприятия и визуализации. 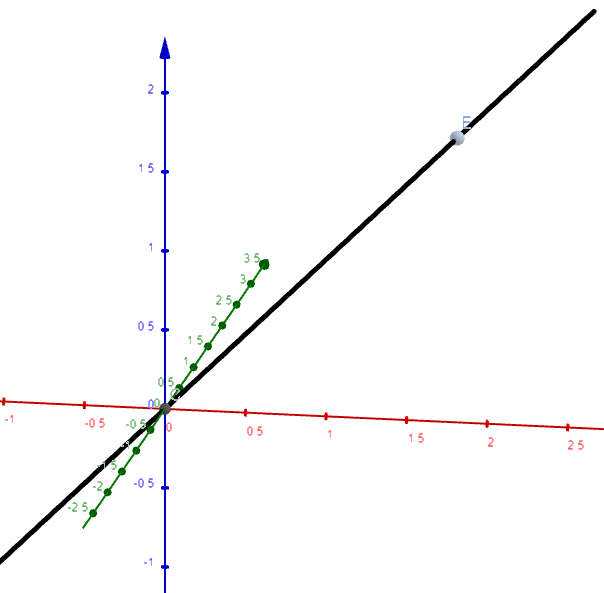 Для перехода в 4 измерение и выше, нам нужно добавить на уже существующий граф четвёртую ось, которую невозможно будет описать, используя уже имеющиеся. Что не представляется возможным. А значит мы даже не можем представить, как выглядит 4 измерение. Однако, мы всё ещё можем описать каждую точку 3 измерения, как точку 4 измерения вида (x, y, z, w). А также зафиксировав значение w, мы получим проекцию на 3 измерение. 6.Задача с n ∈ ℕ, n>3 6.1 К сожалению, по понятным причинам получить изображение данной конструкции не представляется возможным, однако это не помешает найти радиус центральной гиперсферы. Он всё ещё будет равен расстоянию до вершины гиперкуба – 1. Считая, что вершина куба совпадает с вектором 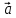 , мы можем записать расстояние до этой точки как , мы можем записать расстояние до этой точки как 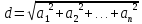 . А так как в нашем случае ребро гиперкуба равно 2, то . А так как в нашем случае ребро гиперкуба равно 2, то 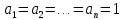 . Иначе говоря, . Иначе говоря, 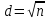 . А значит искомый r = . А значит искомый r = 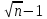 . .Но в тоже время уже при n = 4, это создаёт парадоксальную ситуацию для третьего измерения, ведь если r = 1, то гиперсфера касается стороны куба. И чем больше n, тем меньше отношение объёма сфера внутри куба к внешней части. 6.2 Начнём с нижней оценки. Отметим, что если расположить единичные сферы с координатами (± 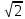 , ± , ±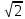 , 0, 0) и всех возможных их вариациях, то у нас будет 24 сферы, касающиеся данной, что очевидно. И они не будут пересекаться. Проверено при помощи программы. K(4) ≥ 24 , 0, 0) и всех возможных их вариациях, то у нас будет 24 сферы, касающиеся данной, что очевидно. И они не будут пересекаться. Проверено при помощи программы. K(4) ≥ 24Для верхней оценки можем сказать, что площадь 4-мерной сферы 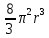 , когда площадь проекции , когда площадь проекции 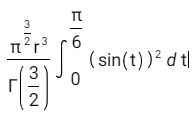 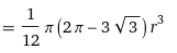 И максимальное количество сфер 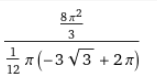 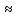 92.4 =>24 ≤ K(4) ≤ 92 92.4 =>24 ≤ K(4) ≤ 92Однако есть доказательство, что K(4) = 24 Заключение. В своей работе, я вычислил контактное число для пространств с размерностью от 1 до 4 при помощи программы на Python и онлайн калькулятора. И это было достаточно увлекательно вычислять, а осознание того, что достаточно небольшое количество людей знает об этой задаче и ещё меньшее пыталось её решить, делает эту работу ещё привлекательнее. Некоторые математики считают так же, поэтому провели верхнюю и нижнюю оценки контактного числа до размерности 24. 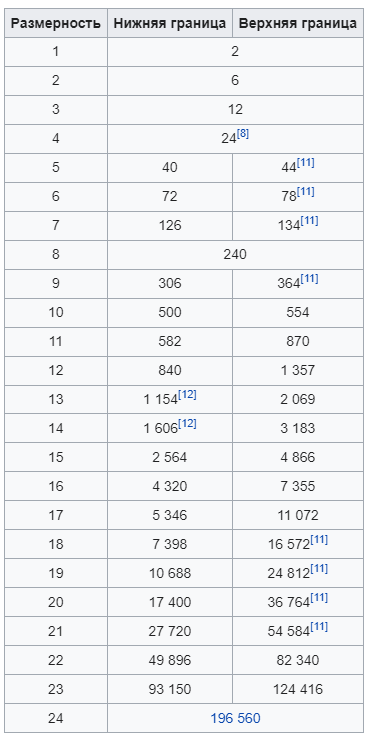 Можно заметить, что для 8 и 24 измерений есть точные результаты. Это заслуга многих учёных, но конечные доказательства привели Коркин и Золотарёв для 8 и Джон Лич для 24. С появлением вычислительных машин, появилась возможность проверять возможные позиции и высчитывать верхние границы. Очевидно, что алгоритмы далеко не самые эффективные и достаточно время затратные, но рабочие, а это главное. Список литературы 1.Мусин О.Р. Проблема 25 сфер. Доказательство К(4) = 24 2..Яглом И. М. Проблема тринадцати шаров. 12 с.Доказательство К(3) ≠ 14 3.Главный источник информации - https://ru.wikipedia.org/wiki/ 4.Площадь 4-мерной сферы и её сегмента https://scialert.net/abstract/?doi=ajms.2011.66.70 5.Данные для таблицы с верхними и нижними границами https://arxiv.org/abs/0902.1105 6.Программа с вычислениями https://colab.research.google.com/drive/1a2qQm45Vif8WHR2d6WnwhwTRwo_OuNxH?usp=sharing |
