Научно- практическая работа по математике Танграмм. РАБОТА Стегалиной С.. Окружная научная конференция учащихся секция "математика"
 Скачать 310.43 Kb. Скачать 310.43 Kb.
|
|
ОКРУЖНАЯ НАУЧНАЯ КОНФЕРЕНЦИЯ УЧАЩИХСЯ СЕКЦИЯ “МАТЕМАТИКА” Использование танграма при изучении темы площади. Автор: Стегалина Светлана учащаяся 6 класса ГБОУ СОШ п. Коммунарский Научный руководитель: Бурухина О.Ф. учитель математики п. Коммунарский, 2015 г. Содержание. Введение……………………………………………………………….3 стр. Историческая справка о танграме……………………………………………………………4 стр. Значение танграма в жизни человека……………………………………………………………6 стр. Площадь и свойства площадей с использованием танграма…...8 стр Математика и танграм нашем современном мире…………………………………………………………………9 стр. Заключение…………………………………………………………….10стр. Список источников информации…………………………………………………………….11стр. Приложение…………………………………………………………….12 стр. ВВЕДЕНИЕ. Наш современный мир переполнен техническими новинками, наш быт модернизирован, роботы научились думать и решать, а порой заменяют самих людей. Мир вокруг становится техническим, а душевная теплота уходит постепенно в небытие. Порой в самом простом можно найти необычное и увлекательное, даже в обыкновенной игре. Несколько лет назад я познакомилась с волшебной игрой Танграм. Слово ТАНГРАМ в переводе с китайского 七巧板, пиньинь qī qiǎo bǎn, буквально «семь дощечек мастерства» — головоломка, состоящая из семи плоских фигур, которые складывают определённым образом для получения другой, более сложной, фигуры (изображающей человека, животное, предмет домашнего обихода, букву или цифру и т. д.). В процесс знакомства и овладения техникой складывания фигурки танграма у меня возникли вопросы: Как танграм может помочь в изучении математики? В решении логических и занимательных математических задач? Цель: изучить взаимосвязь танграма – древней китайской игры-головоломки и математики, точной науки. Гипотеза: Танграм, даёт возможность, правильно понимать и решать математические задачи, связанные с измерением площади. Задачи: на 2013-2014 уч.год Найти, изучить и отобрать информацию по теме. Изучить историю происхождения традиционной китайской игры-головоломки – ТАНГРАМ. Пробудить одноклассников интерес к танграму и занимательной математике. Оформить исследовательскую работу и подготовить презентацию. на 2014-2015 уч.год: Продолжить изучение информации по теме. Пробудить интерес к танграму и занимательной математике учащихся 2,3 и 5 классов. Провести соревнование по собиранию из танграма фигурок, между одноклассниками и классами нашей школы. Проследить взаимосвязь между овладением приёмами собирания фигур и обучением учащихся 2,3, 5 и 6 классов. Оформить исследовательскую работу и подготовить презентацию. Объект исследования: танграм. Методы исследования: Изучение литературы и сведений и различных информационных источников. Наблюдение. Обработка полученных данных. Нахождение площадей простейших фигур, с использованием танграма. Анкетирование учащихся и учителей.(приложение №3) Анализ и обобщение информации по теме. История танграма О названии Танграм В Китае название Танграм неизвестно, а игра имеет название Ши-Чао-Тю (семь хитроумных фигур). В Оксфордском словаре английского языка — название Танграм появляется с ссылкой на авторитетного Генри Э.Дьюдени, его версию принял составитель словаря Д.Мюррей. Он обнаружил, что слово танграм впервые встречается в словаре Вебстера издания 1864 г. По мнению в Мюррея, само слово танграм было придумано в середине прошлого столетия неким американцем, образовавшим неологизм из слова Тан, что означает на кантонском диалекте китайский, и распространенного суффикса -грам (как в словах анаграмма или криптограмма). Иная теория происхождения слова танграм была выдвинута Питером Ван Ноутом в предисловии к новому изданию книги Ллойда: китайские семьи, живущие на лодках, называются танка, тан по-китайски означает — падшая женщина. Американские моряки, покупавшие головоломку у девушек — танка, могли назвать ее танграмом — головоломкой доступных девушек. В книге «Китайский философский и математический транграм» (1817 г.) слово транграм — трактуется, как старинное английское слово — обозначающие игрушка головоломка. Миф создания Существует целый ряд версий и гипотез возникновения игры “Танграм”. 1) Наиболее распространенной и известной является та, что игра “Танграм” насчитывает около 4000 лет. Такую дату можно прочитать у Кордемского Б.А. или Котова А.Я., а так же у различных иностранных авторов. Мнение о танграме, как о самой древней головоломке является весьма распространенным. Однако, это всеобщее заблуждение. Миф об этом создал С.Лойд. В 1903 году он выпустил книгу “Восьмая книга Тана”, в которой впервые опубликовал свою красивую версию о древнем происхождение игры. Это и по настоящее время один из величайших розыгрышей в мире головоломок. 2) Местом где была изобретена игра, несомненно является Китай. Дата создания может быть определенна приблизительно XVIII век. Первой известной древней книгой по танграму является “Собрание фигур из семи частей” (Китай 1803 г.). Издана она была на рисовой бумаге. Книги, изданные в Европе, были лишь отчасти оригинальны, а в своей основе имели китайские источники. “В записках покойного профессора Челленора, попавших в руки автора, — утверждал Лойд, — имеются сведения о том, что семь книг о танграмах, каждая из которых насчитывает ровно тысячу фигур, были составлены в Китае более 4000 лет назад. Эти книги ныне стали столь большой редкостью, что за те сорок лет, которые профессор Челленор провел в Китае, ему лишь раз удалось видеть первое издание первого из семи томов (сохранившихся полностью) и несколько разрозненных фрагмента второго тома. В этой книге связи уместно напомнить, что части одной из книг, напечатанной золотом на пергаменте, были обнаружены в Пекине английским солдатом, продавшим свою находку за 300 фунтов стерлингов одному собирателю китайской старины, который любезно предоставил некоторые наиболее изысканные фигурки для воспроизведения в этой книге”. Согласно легенде Лойда, Тан был легендарным китайским мудрецом, которому его соотечественники поклонялись как божеству. Фигуры в своих семи книгах он расположил в соответствии с семью стадиями в эволюции Земли. Его танграмы начинаются с символических изображений хаоса и принципа “инь и ян”. Затем следуют простейшие формы жизни, по мере продвижения по древу эволюции появляются фигуры рыб, птиц, животных и человека. По пути в различных местах попадаются изображения того, что создано человеком: орудию труда, мебель, одежда и архитектурные сооружения. Лойд часто цитирует высказывания Конфуция, философа по имени Шуфуце, комментатора Ли Хуанчжан и вымышленного профессора Челленора. Ли Хуанчжан упоминается в связи с тем, что по преданию он знал все фигуры из семи книг Тана прежде, чем научился говорить. Встречаются у Лойда и ссылки на “известные” китайские пословицы типа “Только глупец взялся бы написать восьмую книгу Тана”. Знаменитые люди и танграм Льюис Кэрролл Все мы хорошо знаем книгу «Алиса в стране чудес» Л.Кэрролла (Чарльз Лютвидж Доджсон). Однако это его не единственное произведение. В книге «Модная китайская головоломка» он пишет, что танграм был любимой игрой Наполеона, который, лишившись трона, в изгнании проводил долгие часы за этой забавой, «упражняя свое терпение и находчивость». Упоминание о любимой игре Наполеона, скорее всего не соответствует действительности, однако, и нет обратных доказательств, что, в свою очередь, позволяет существовать и такой красивой версии. Эдгар А. По Одним из поклонников игры был Эдгар А. По. Принадлежавший ему танграм сделан из слоновой кости и в настоящее время хранится в Нью-Йоркской публичной библиотеке. Роберт ван Гулик Известный писатель и дипломат Роберт ван Гулик в романе «Убивающие ногтями» построил весь сюжет книги вокруг танграма. Абдул — Вефа Одним из первых научных трудов известных человечеству по решению задач на разрезание является трактат Абдул Вефа. Он являлся персидским астрономом. Жил в десятом веке в Багдаде. Сохранились лишь отдельные части этой книги и в том числе решение задачи как разрезать три одинаковых квадрата на 9 частей из которых в дальнейшем возможно сложить один большой квадрат. В дальнейшем решение этой задачи с условием использования минимального количества элементов было сделано англичанином Генри Э. Дьюдени. Он решил задачу Абдул Вефа с использованием 6 элементов, и это является минимальным решением на настоящее время. Гарри Линдгрен Энциклопедией решения различных задач на разрезание является книга Гарри Линдгрена «Геометрия разрезаний». В этой книге можно найти рекорды по разрезанию многоугольников на заданные фигуры. При использовании треугольника как базового элемента — многоугольники можно разрезать на следующие количество частей: квадрат — 4 пятиугольник — 6 шестиугольник — 5 семиугольник — 9 восьмиугольник — 8 девятиугольник — 9 десятиугольник — 8 двенадцатиугольник — 8 Рассматривая решения задач на разрезание понимаешь, что универсального алгоритма или метода не существует. Иногда начинающий геометр в своем решении может значительно превзойти более опытного человека. Это простота и доступность является основой популярности игр основанных на решении таких задач. Сразу на ум приходит пример — тетрис. Площадь и свойства площадей с использованием танграма. Изучая тему в 5 классе «Площадь. Свойства площадей.» Можно чётко проследить данное понятие на примере «Танграма». Собрав квадрат, становиться ясно, что измерение части занимаемой той или иной фигурой, удобно осуществлять квадратом, с заданной единицей длины стороны квадрата. Свойства площадей: 1.Равные фигуры имеют равные площади. С помощью наложения треугольников в танграме это хорошо просматривается. Треугольник аbd = треугольнику adh, 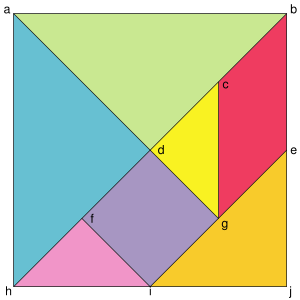 Треугольник hfi= треугольнику dgc. Треугольник hfi= треугольнику dgc.2.Чтобы найти площадь сложной фигуры надо найти сумму всех площадей входящих в неё фигур. В танграмме, площадь фигуры cbeg= площадь треуголника cgd+ площадь треугольника hti, а так как площади этих треугольников равны, то площадь четырёхугольника cbeg=2 площадям треугольникаcgd.Площадь треугольника iej=2площадям cgd.Таким образом площадь четырёхугольника cbeg=площади треугольника iej. Проведём исследование на примере измерения площади танграма. Танграм в собранном квадрате имеет площадь: S =8,1*8,1=65,61см.² Если разделить квадрат пополам, то площади полученных двух треугольников будут равны, об этом говорилось выше, т.е. площадь одного треугольника будет равна 65,61:2=32,805см².Четвертая часть площади всего квадрата равна 65,61:4=16,4025 см² или 32,805:2=16,4025см². Удивительно, но площадь оставшейся четвертинки равна сумме площадей, входящих в неё маленьких фигурок, равных по наложению, т.е. четырём маленьким треугольникам.Sтр.=1/4*16,4025=4,100625см².Следовательно, площади маленького квадрата iqdt=S четырёхугольника qcbe=S треугольникаiej=4,100625*2=8,20125см². Вывод: Действительно тема площадей и свойств площадей прекрасно иллюстрируется танграмом . Значение оригами в жизни человека. Пазлы Игрой внешне близкой танграму являются пазлы. В начале пазлы являлись большим набором фигур неправильной формы из которых необходимо было сложить картинку — задание. Несмотря на эту схожесть — танграм, задача противоположная, так как семь базовых элементов позволяет значительное множество фигур, а в случае пазла мы ограничены только одним решением. Сравнительный анализ танграма с другими аналогичными играми был сделан Р.Ридом в книге «Танграмы: 330 головоломок». Для игры танграм основным требованием к человеку является логическое мышление и геометрическая интуиция, а для игры пазл — все-таки всего лишь усидчивость и терпение. Розыгрыш Дьюдени В своей книге «Математические развлечения» он приводит вымышленную историю о том, как один американский корреспондент приобрел набор перламутровых танов китайской работы, к которому прилагалось отпечатанная на рисовой бумаге брошюра, содержавшая более 300-х фигур. Корреспондента заинтересовал таинственный иероглиф на титульном листе, но все китайцы, к которым он обращался с просьбой объяснить, что означает этот знак, не хотели или не могли ничем ему помочь. Он воспроизвел иероглиф в своей книге и обратился к читателям за помощью. Мы знаем, что ответили Дьюдени его современники, но Рид, у которого была та же брошюра, без труда разгадал загадку. Иероглиф был просто надписью под танграмом, изображавшим двух человек. Надпись гласила — два человека лицом друг к другу пьют чай. Эта картинка свидетельствовала о больших возможностях, таящихся в игре танграм. Танграм. Новые идеи и возможности головоломки
Танграм во всех его проявлениях можно встретить: начиная от дизайна одежды, заканчивая архитектурой и ландшафтным дизайном. Самое удачное применение танграма, пожалуй, в качестве мебели. Есть и столы танграмы и трансформируемая мягкая мебель и знаменитые настенные полки фирмы Lago.
Вся мебель, построенная по принципу танграма очень удобна и функциональна. Каждый раз она может видоизменятся, в зависимости от настроения и желания хозяина. Интересный вариант трансформируемых диванов дизайнера Julien Bernard. Эта модель была представлена на выставке в Милане в 2009 году. Самая известная коллекция мебели в стиле танграм у дизайнеров по интерьерам - конечно, Lago. Сколько всевозможных вариантов и комбинаций можно составить из этих симпатичных полочек. Сами производители выпустили вместе с инструкцией по сборке несколько страниц с идеями для библиотеки, гостиной, спальни и детской. Заключение 1.Танграм способствует развитию у детей: умения играть по правилам и выполнять инструкции, умения наглядно - образно мыслить, воображать, вниманию. пониманию цвета, величины и формы, восприятия, комбинаторных способностей. 2. Тема площадей и свойств площадей прекрасно иллюстрируется танграмом . ИСТОЧНИКИ ИНФОРМАЦИИ The Tangram Book. — Sterling Publishing Company, 2003. — ISBN 1-4027-0413-5 puzzles.h1.ru/Puzzles/tangram.html www.babylessons.ru/igra-golovolomka-tangram/ ru.wikipedia.org/wiki/Танграм www.printplay.ru/tangram-novye-idei…vozmozhnosti… Приложение №1   Приложение №2    Приложение №3 Проведена анкета 14.10.2014 года, среди учащихся - 2, 3, 5 и 6 классов- 42 человека, взрослых -16 человек, с вопросами:  Вы знаете, что такое танграм? Вы играли в эту головоломку? Вам понравилась эта игра? Результаты в таблице.  1 2 3 3 Вопрос ы 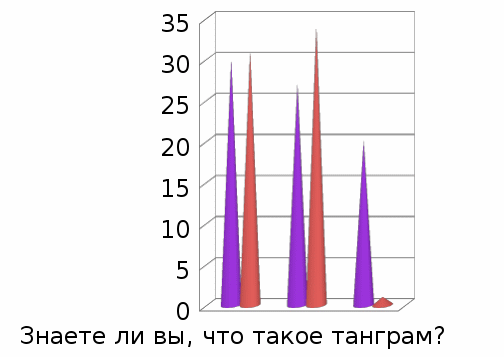 Приложение №4. С10.09 по 23 декабря 2014года учащиеся 2,3 и 5 классов учились составлять 10 основных фигурок из танграма за 1 минуту.(квадрат, прямоугольник, параллелограмм, 3кошечек, бегущего человечка, зайчика, рыбку, собачку)Результаты первого входного соревнования, проведенного 24.12.2014г. следующие:
Результаты второго соревнования, проведенного 9.02.2015г. следующие:
Вывод: На протяжении 4 месяцев учащиеся 2, 3, 5кл. научились игре –головоломке «Танграм» и с 6 классом повысили скорость собирания 10 фигурок танграма. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||



