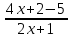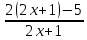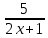|
|
Омарова Гульзира Сулейменовна ызылорда аласы 212 мектепгимназиясыны жоары санатты математика пніні малімі
Омарова Гульзира Сулейменовна – Қызылорда қаласы №212 мектеп-гимназиясының
жоғары санатты математика пәнінің мұғалімі
«Алгебра» пәнінен І тоқсан бойынша жиынтық бағалау тапсырмаларының сипаттамасы
Бөлім
|
Тексерілетін мақсат
|
Ойлау дағдыларының деңгейі
|
Тапсырма саны
|
№ тапсырма
|
Тапсырма түрі
|
Орындалу уақыты,мин
|
Балл
|
Бөлім бойынша балл
|
Функция, оның қасиеттері және графигі
|
10.4.1.4 Функцияның берілген графигі бойынша оның қасиеттерін:
1) функцияның анықталу облысы;
2) функцияның мәндер жиыны;
3) функцияның нөлдері;
4) функцияның периодтылығы;
5) функцияның бірсарындылық аралықтары;
6) функцияның таңбатұрақтылық аралықтары;
7) функцияның ең үлкен және ең кіші мәндері;
8) функцияның жұптылығы, тақтылығы;
9) функцияның шектелгендігі;
10) функция үзіліссіздігі;
11) функцияның экстремумдары сипаттай алу;
|
Қолдану
|
1
|
1
|
ҚЖ
|
7
|
5
|
11
|
10.4.1.5 у=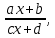 c c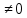 бөлшек-сызықты функциясының қасиеттерін анықтау және оның графигін салу; бөлшек-сызықты функциясының қасиеттерін анықтау және оның графигін салу;
|
Қолдану
|
1
|
7
|
ТЖ
|
4
|
3
|
10.4.1.7 - f(g(x)) күрделі функциясын ажырата білу және функциялар композициясын құру;
|
Қолдану
|
1
|
6
|
ТЖ
|
6
|
3
|
Тригонометриялық функциялар
|
10.2.3.1 Тригонометриялық функциялар анықтамаларын, қасиеттерін білу және олардың графиктерін сала білу;
|
Қолдану
|
1
|
4а
|
ТЖ
|
3
|
1
|
4
|
10.2.3.2 Тригонометриялық функциялардың графиктерін түрлендірулер көмегімен сала білу
|
Қолдану
|
4ә
|
ТЖ
|
5
|
3
|
Кері тригонометриялық функциялар
|
10.2.3.3 Арксинус, арккосинус, арктангенс, арккотангенс анықтамаларын білу және олардың мәндерін таба білу
|
Білу және түсіну
|
1
|
2
|
ТЖ
|
5
|
3
|
10
|
10.2.3.6 Кері тригонометриялық функциялары бар өрнектерді түрлендірулер орындау;
|
Қолдану
|
1
|
5
|
ТЖ
|
5
|
3
|
10.2.3.7 Кері тригонометриялық функциялары бар қарапайым теңдеулерді шеше алу;
|
Қолдану
|
1
|
3
|
ТЖ
|
5
|
4
|
Барлығы:
|
|
|
7
|
|
|
40
|
|
25
|
1-тоқсанға арналған жиынтық бағалаудың тапсырмалары
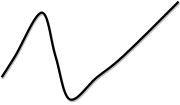
Графикті қолданып ,функцияның қасиеттерін жазыңдар:
(әрбір тор көз бірлік кесінді ретінде алынған)
а) анықталу облысы; ә) мәндер жиыны; б) нөлдері;
в) таңба тұрақтылық аралықтары;
г) өсу, кему аралықтарын табыңыз. 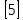
2. Өрнектің мәнін табыңдар: arccos (-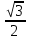 ) –arcsin ) –arcsin 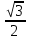 ; [3] ; [3]
3. Теңдеуді шешіңдер: 2 arcsin (5x-1)= - 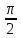 ; [4] ; [4]
4. а) y=sin x функциясының [ 0; 2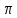 ] аралығындағы графигін салыңдар [1] ] аралығындағы графигін салыңдар [1]
ә) у=sin (х-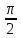 ) + 1 функциясының графигін салыңдар [3] ) + 1 функциясының графигін салыңдар [3]
5. Есептеңдер: sin (2 arccos 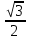 ); [3] ); [3]
6. f1(x) = x2+1, f2(x)=2x, f3(x)=x-2 функциялары берілген, х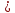 0. [3] 0. [3]
Есептеңдер: f1(f2(х))- f1(f3(х));
7. y=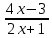 функциясы берілген. Берілген функцияны y=P- функциясы берілген. Берілген функцияны y=P-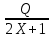 түрінде жазыңыз, мұндағы Р мен Q – бүтін сандар. [3] түрінде жазыңыз, мұндағы Р мен Q – бүтін сандар. [3]
Балл қою кестесі
№
|
Жауап
|
Балл
|
Қосымша ақпарат
|
1a
|
D (f) =[-7;6]
|
1
|
|
1ә
|
Е (f)= [-4;5]
|
1
|
|
1б
|
(-6;0), (-3;0), (2;0)
|
1
|
|
1в
|
f(х)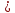 0, (-6;-3) 0, (-6;-3)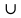 (2;6) (2;6)
|
1
|
|
f(х)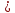 0, (-7;-6) 0, (-7;-6)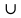 (-3;2) (-3;2)
|
1
|
|
1г
|
Өсу: [-7;-4]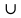 [-2;6] [-2;6]
|
1
|
|
Кему: [-4;2]
|
1
|
|
2
|
arccos (-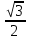 ) =π - ) =π - 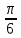 = = 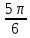
|
1
|
|
arcsin 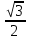 = = 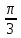
|
1
|
|
arccos (-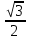 ) –arcsin ) –arcsin 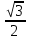 = = 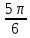 - - 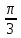 = = 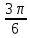 = = 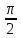
|
1
|
|
3
|
arcsin(5x-1)= - 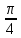 ; ;
|
1
|
|
5x-1= - 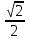
|
1
|
|
5x= 1- 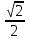 ; ;
|
1
|
|
х= 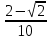 ; ;
|
1
|
|
4а
|
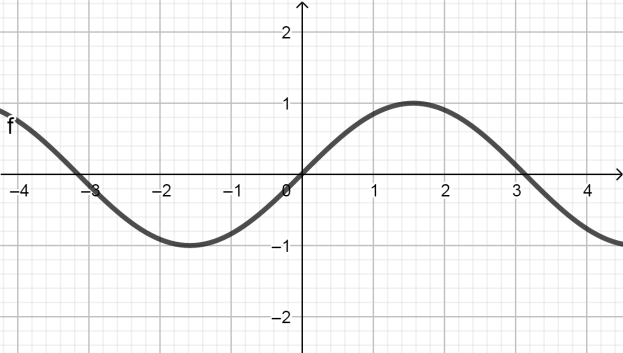
|
1
|
y=sin x функциясының графигін салды
|
4ә
|
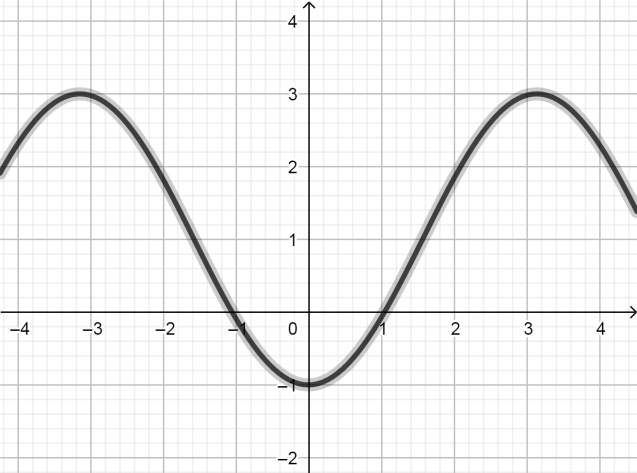
|
1
|
Графикті Оу осі бойымен 2 есе созып,у=sin x функциясының графигін алды
|
1
|
Шыққан графикті Ох осі бойымен 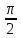 қашықтықта оң бағытта параллель көшіріп, у= sin (х- қашықтықта оң бағытта параллель көшіріп, у= sin (х-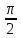 ) )
функциясының графигін алды
|
1
|
Ең соңғы графикті Оу осі бойымен жоғары бір бірлікке параллель көшіріп, у=sin (х- ) + 1 функциясының графигін алды ) + 1 функциясының графигін алды
|
5
|
2sin ( arccos 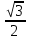 ) * cos (arccos ) * cos (arccos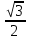 ) )
|
1
|
sin (2 * 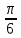 )= sin )= sin 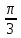 = = 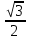
|
2sin ( arcsin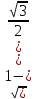 * cos (arccos * cos (arccos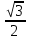 ) )
|
1
|
|
2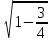 * *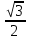 = = 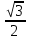
|
1
|
|
6
|
f1(f2(х))=(2x)+1=4x2+1
|
1
|
|
f1(f3(х))=(x-2)2+1=x2-4x+4+1=x2-4x+5
|
1
|
|
f1(f2(х))- f1(f3(х))= 4x2+1- x2+4x-5=3x2+4x-4
|
1
|
|
7
|
y=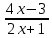 = =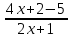
|
1
|
|
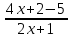 = =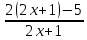
|
1
|
|
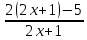 =2- =2-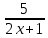
|
1
|
| |
|
|
 Скачать 123.66 Kb.
Скачать 123.66 Kb.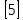
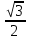 ) –arcsin
) –arcsin 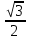 ; [3]
; [3] 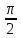 ; [4]
; [4] 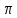 ] аралығындағы графигін салыңдар [1]
] аралығындағы графигін салыңдар [1]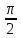 ) + 1 функциясының графигін салыңдар [3]
) + 1 функциясының графигін салыңдар [3]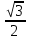 ); [3]
); [3] 0. [3]
0. [3]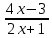 функциясы берілген. Берілген функцияны y=P-
функциясы берілген. Берілген функцияны y=P-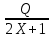 түрінде жазыңыз, мұндағы Р мен Q – бүтін сандар. [3]
түрінде жазыңыз, мұндағы Р мен Q – бүтін сандар. [3]
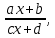 c
c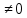 бөлшек-сызықты функциясының қасиеттерін анықтау және оның графигін салу;
бөлшек-сызықты функциясының қасиеттерін анықтау және оның графигін салу;

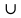 (2;6)
(2;6)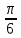 =
= 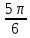
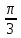
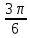 =
= 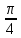 ;
;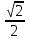
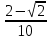 ;
;

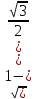 * cos (arccos
* cos (arccos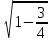 *
*