Описанная и вписанная окружности около треугольника
 Скачать 154.91 Kb. Скачать 154.91 Kb.
|
|
Класс: 7 Тема урока: Описанная и вписанная окружности около треугольника Тип урока: изучение нового учебного материала. Цели: Предметные - познакомить учащихся с понятиями вписанной и описанной окружностей треугольника и их свойствами. Личностные - формировать интерес к изучению темы и желание применять приобретённые знания и умения. Метапредметные - формировать умение использовать приобретённые знания в практической деятельности. ХОД УРОКА: I.Организационный момент. (Проверка домашнего задания, наличия учебников и тетрадей. Урок проводится с помощью презентации ). II.Актуализация знаний. Устный опрос. 1) Что такое окружность? 2) Дайте определение треугольника? 3) Что такое перпендикуляр? 4) Что такое серединный перпендикуляр? 5) Что такое касательная? 6) Что такое биссектриса треугольника? III. Постановка цели и задач урока. Мотивация учебной деятельности. IV. Изучение нового материала. О 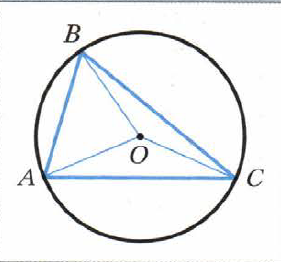 пределение: Окружность называют описанной около треугольника, если она проходит через все вершины этого треугольника. пределение: Окружность называют описанной около треугольника, если она проходит через все вершины этого треугольника.ОА=ОВ=ОС=R Говорят также, что треугольник вписан в окружность. Теорема 21.1 Около любого треугольника можно описать окружность. П 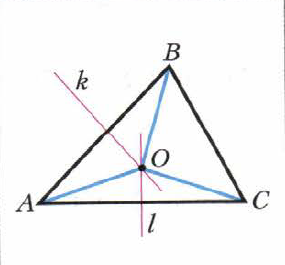 рактическая работа. Построить произвольный треугольник АВС. Провести серединные перпендикуляры m и n и k к сторонам АВ, АС и ВС соответственно. Что можно сказать о взаимном расположении серединных перпендикуляров? рактическая работа. Построить произвольный треугольник АВС. Провести серединные перпендикуляры m и n и k к сторонам АВ, АС и ВС соответственно. Что можно сказать о взаимном расположении серединных перпендикуляров?Следствие 1. Три серединных перпендикуляра сторон треугольника пересекаются в одной точке. Обозначить точку пересечения буквой О. Т. к. точка О принадлежит серединному перпендикуляру m, то ОА=ОВ. Поскольку точка О принадлежит серединному перпендикуляру n, то ОА=ОС. Значит ОА=ОС=ОВ, т. е. тоска О равноудалена от всех вершин треугольника. Около треугольника можно описать только одну окружность, т. к. серединные перпендикуляры имеют только одну точку пересечения. Провести окружность с центром в точку О. Что можно сказать о взаимном расположении треугольника и окружности?. Следствие 2. Центр окружности, описанной около треугольника, – это точка пересечения серединных перпендикуляров его сторон. 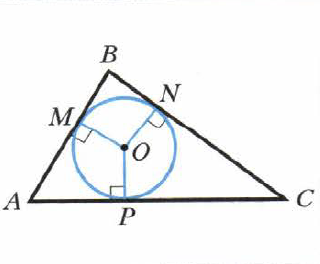 Определение: Окружность называют вписанной в треугольник, если она касается всех его сторон. В этом случае также говорят, что треугольник описан около окружности. Точка О (рис. 301) — центр вписанной окружности треугольника АВС, отрезки ОМ, ON, OP - радиусы, проведённые в точки касания, ОМ 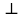 AB, ON AB, ON 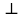 ВС, OP ВС, OP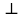 AC. Поскольку ОМ = ON=OP, то центр вписанной окружности треугольника равноудалён от всех его сторон. AC. Поскольку ОМ = ON=OP, то центр вписанной окружности треугольника равноудалён от всех его сторон.Теорема 21.2 В любой треугольник можно вписать окружность. Практическая работа. Построить произвольный треугольник АВС. Провести биссектрисы углов А и В., Обозначить точку их пересечения буквой О. Т. к. точка О принадлежит биссектрисе угла А, то она равноудалена от сторон АВ и АС.(теорема 19.2). Аналогично, так как точка О принадлежит биссектрисе угла В, то она равноудалена от сторон ВА и ВС. Следовательно, точка О равноудалена от всех сторон треугольника. Заметим, что в треугольник можно вписать только одну окружность. Это следует из того, что биссектрисы углов А и В (см. рис. 302) пересекаются только в одной точке. Следовательно, существует только одна точка, равноудалённая от сторон треугольника. Следствие 1. Биссектрисы углов треугольника пересекаются в одной точке. Следствие 2.Центр окружности, вписанной в треугольник, — это точка пересечения его биссектрис. V. Первичное закрепление нового материала. № 540, 545, 548. VI .Итог урока Какая окружность называется описанной около треугольника? Какой треугольник называют вписанным в окружность? Около какого треугольника можно описать окружность? Какая точка является центром окружности, описанной около треугольника? Какую окружность называют вписанной в треугольник? Какой треугольник называют описанным около окружности? В какой треугольник можно вписать окружность? Какая точка является центром окружности, вписанной в треугольник? ( дать качественную оценку работы класса и отдельных учащихся). VII. Информация о домашнем задании. §21, вопр 1-8. № 541, 545. РТ №294-299 |
