Статья демпфер-ВЧ-3. Определение демпфирующих характеристик конструкции со сложной структурой
 Скачать 0.84 Mb. Скачать 0.84 Mb.
|
|
УДК 539.3 ОПРЕДЕЛЕНИЕ ДЕМПФИРУЮЩИХ ХАРАКТЕРИСТИК КОНСТРУКЦИИ СО СЛОЖНОЙ СТРУКТУРОЙ © 2013 г. Н.Н. Берендеев¹, Н.В. Зимин2, Н.В. Леонтьев¹, А.К. Любимов¹, И.А. Смирнов², Е.В. Сторожев², ¹Нижегородский государственный университет им. Н.И. Лобачевского ²ЗАО «Время-Ч» ljubimov@mm.unn.ru Поступила в редакцию Предложена экспериментально-расчетная методика определения демпфирующих характеристик сложных конструкций с использованием вибростенда Star28х, обеспечивающего трехмерное псевдослучайное нагружение, и методов численного моделирования. Приведены результаты исследований для конструкции. Ключевые слова: вибростенд, трехмерное псевдослучайное нагружение, матрица демпфирования, Введение Уравнение колебаний линейной распределённой системы имеет следующий вид [1,2] 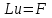 , (1) , (1)где  - линейный оператор, - линейный оператор, 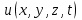 - вектор перемещения, - вектор перемещения,  - вектор внешних воздействий. - вектор внешних воздействий.Одним из наиболее распространенных методов численного анализа конструкций является метод конечных элементов (МКЭ). В этом случае уравнение (1) представляется, как матричное уравнение движения системы конечных элементов, и может быть записано в виде [3] 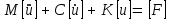 , (2) , (2)где [M] – матрица масс, [C] – матрица демпфирования,[K] – матрица жесткости,  –соответственно вектора ускорений, скоростей и перемещений в узлах, [F]– вектор приложенных внешних усилий. –соответственно вектора ускорений, скоростей и перемещений в узлах, [F]– вектор приложенных внешних усилий.Матрица демпфирования определяет диссипацию энергии конструкции.Формально матрицу можно получить, аналогично матрицам жесткости и масс, вводя из каких-либо дополнительных предположений константу внутреннего трения и суммируя соответствующие матрицы элементов. Наибольший интерес при анализе поведения силовых конструкций как правило представляет учет сухого трения и гистерезисного (внутреннего) демпфирования, а не вязкого трения. В этом случае матрица демпфирования аппроксимируется линейной комбинацией вкладов сопротивлений, связанных с двумя матрицами системы - матрицей масс и матрицей жесткости: [C] = [M] + [K], (3) где коэффициенты и определяются как константы демпфирования Рэлея. Параметр характеризует инерционное демпфирование, а параметр - конструкционное.Значения параметров требуют определения в каждом конкретном случае. 1.Методика определения демпфирующих характеристик конструкции Одним из основных параметров, определяющих поведение конструкции в условиях гармонического воздействия, случайной вибрации и динамического поведения (переходных процессов), являются её демпфирующие характеристики. В настоящее время существует ряд методик, позволяющих оценить данные характеристики. Рассмотрим некоторые методики, с учетом их применимости для оценки демпфирующих характеристик сложных конструкции. В основу первого подхода положено предположение о том, что демпфирующие характеристики полностью описываются внутренним трением элементов конструкции, связанным с гистерезисными потерями [4], и, так называемым, конструкционным демпфированием [4], определяемым сухим трением в узлах сопряжения в конструкции. При применении указанного подхода возникают две проблемы, затрудняющие его использование: во-первых, конструкция как правило выполнена из различных материалов и для большинства их них отсутствуют сведения о гистерезисных потерях, то есть требуются дополнительные экспериментальные исследования образцов материалов, во-вторых, конструкция состоит из большого количества элементов, между которыми присутствуют связи, поэтому итоговая комбинация будет избыточно сложной. В основу второго подхода положен анализ поведения конструкции при вынужденных гармонических колебаниях [4]. По результатам экспериментального исследования конструкции в указанных условиях строится амплитудно-частотная характеристика, на которой выбирается единичный пик, соответствующий резонансу, определяется его ширина на высоте двух третей от высоты пика и по известным соотношениям [4] находится логарифмический декремент затухания. Данный метод эффективен для достаточно простых систем. В случае же сложных систем состоящих из значительного числа взаимодействующих элементов, за счет плотного расположения собственных частот, достаточно часто невозможно выделить уединенный пик, что приводит к серьёзным затруднениям при использовании методики. В основе третьего подхода [5] лежит обработка виброграммы конструкции в условиях собственных затухающих колебаний и исследование ее огибающей. Для определения демпфирующих характеристик сложной конструкции включающей значительное число взаимодействующих элементов, поведение которой описывается уравнением (2), предлагается расчётно-экспериментальная методика, основывающаяся на совместном применении методов натурного и численного экспериментов. В основе предлагаемой методики лежат допущения о том, что: во-первых, функция мощности спектральной плотности (МСП), получаемая как отклик конструкции на случайное внешнее воздействие, позволяет определить собственные частоты конструкции [6,7], во-вторых, вид функции мощности спектральной плотности определяется уровнем демпфирования в конструкции. Данный подход с учетом введенных выше допущений о характере демпфирования в конструкции, нацелен на определение величины 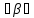 в соотношении (3) для конструкции в целом. Предполагается, что конструкционное демпфирование, возникающее вследствие действия сил сухого трения в соединениях при колебаниях конструкции, значительно более значимо чем демпфирование, создаваемое действием внутреннего трения в материале деталей. В этом случае в соотношение (3) можем положить с достаточной степенью точности в соотношении (3) для конструкции в целом. Предполагается, что конструкционное демпфирование, возникающее вследствие действия сил сухого трения в соединениях при колебаниях конструкции, значительно более значимо чем демпфирование, создаваемое действием внутреннего трения в материале деталей. В этом случае в соотношение (3) можем положить с достаточной степенью точности  Введем два параметра, характеризующих пик на МСП соответствующий собственной частоте (рис.1). 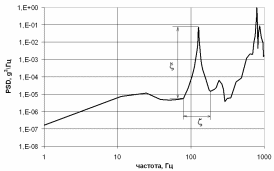 МСП Рис.1 Параметры, характеризующие влияние уровня демпфирования на функцию мощности спектральной плотности Параметр 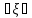 - определяет высоту пика МСП, соответствующего собственной частоте, а параметр - определяет высоту пика МСП, соответствующего собственной частоте, а параметр  - ширину пика в его основании. - ширину пика в его основании. Анализ функций мощности спектральной плотности показал, что уровень демпфирования функционально зависит от величины  . (4) . (4)Предлагаемая расчётно-экспериментальная методика оценки уровня демпфирования сложной конструкции содержит следующие этапы: Экспериментальное определение функций МСП для исследуемой конструкции в конечном числе точек; Анализ полученных в эксперименте данных, выбор наиболее характерной для рассматриваемой конструкции ПСД и определение наиболее значимых  пиков, вычисление для них отношений пиков, вычисление для них отношений  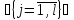 согласно (4); согласно (4);Задание величины допускаемого интервала для общего трения всей системы в целом (т.е. области допустимых значений коэффициента 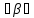 из соотношения (3)) из соотношения (3)) ; (5) ; (5)Замена интервала, определяемого соотношением (5), на его дискретный аналог 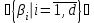 ; (6) ; (6)Численный анализ конструкции с использованием МКЭ при действии случайной нагрузки с заданными свойствами для каждого из значений 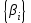 дискретного аналога интервала (6) и построение по его результатам функций мощности спектральной плотности; дискретного аналога интервала (6) и построение по его результатам функций мощности спектральной плотности;Анализ МСП, полученных в численном эксперименте, с целью нахождения пиков соответствующих собственным частотам. Определение для выбранных пиков из расчетных функций мощности спектральной плотности характеристики  согласно (4) для каждого из согласно (4) для каждого из  пиков. пиков. Построение полинома 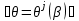 , аппроксимирующего значения отношения для каждого из , аппроксимирующего значения отношения для каждого из  пиков; пиков;Построение свертки  ; (7) ; (7)Определение искомого значения коэффициента  путем минимизации величины свертки (7): путем минимизации величины свертки (7): Полученное значение коэффициента β используется для определения матрицы демпфирования в МКЭ. 2. Результаты экспериментальных исследований 2.1. Вибростенд Star28х Для экспериментального определения функции МСП конструкции в конечном числе точек использовался вибростенд Star28х. Конструкция стенда обеспечивает случайные колебания рабочего стола с шестью степенями свободы. Возбуждение стола производится восемью пневматическими вибраторами, каждый из которых генерирует псевдослучайное ударное нагружение типа «белого шума» в диапазоне частот от 20 до 6500 Гц. Среднеквадратичное отклонение (СКО) ускорения изменяется в диапазоне от 3 до 30 g. Максимальная масса испытываемой конструкции закрепляемой на столе составляет 227 кг. Входящее в состав стенда программное обеспечение, обеспечивает возможность задания истории нагружения, т.е. закона изменения величины СКО с течением времени, осуществляет контроль с помощью датчиков ускорения (ДУ) за точностью реализации программы нагружения, находит численную оценку функции спектральной плотности, выполняет визуализацию реализаций во времени величин ускорения и скорости, а также вычисляет ряд других характеристик. Информация определяется для каждого ДУ. Общее число каналов, к которым подключаются датчики в данной версии стенда равно четырём. ДУ DYTRAN модели 3030В4 позволяют проводить измерения в диапазоне частот от 2 до10000 Гц, резонансная частота датчиков - 30 кГц, максимальное значение вибрации до 1000 g (СКО). 2.2. Колебания рабочего стола Рабочий стол стенда выполнен в виде массивной квадратной металлической плиты размером 711 мм х 711 мм с отверстиями для крепления испытываемой конструкции. С целью изучения характеристик вибрации стола, возникающей под действием вибраторов, на него крепились три ДУ, позволяющие проводить измерения в трех взаимно ортогональных направлениях, а также датчик, контролирующий точность реализации истории нагружения в вертикальном направлении. Направления горизонтальных осей OX, OY были выбраны параллельно сторонам стола, оси OZ – перпендикулярно плоскости стола. История нагружения задавалась в виде постоянного значения СКО равного 15 g в течение 5 минут. В результате проведенных экспериментов [6]получены МСП S 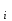  , реализации величины скорости V , реализации величины скорости V и ускорения W и ускорения W , ,  , для различных точек стола, результаты обработки реализаций процесса ускорения методом «падающего дождя». , для различных точек стола, результаты обработки реализаций процесса ускорения методом «падающего дождя». МСП, полученные по трем осям, имеют чётко выраженный пик, что позволяет сделать вывод о узкополосности случайных процессов, описывающих ускорение стола вдоль осей. Предположение об узкополосности подтверждается также характерной формой реализаций процессов величины ускорения вдоль осей. Обработка реализаций процессов ускорений в направлении осей методом «падающего дождя» даёт основание для вывода о том, что одномерные функции распределения значений случайного процесса могут описываться нормальным законом распределения. Для оценки стабильности получаемых результатов при заданной истории нагружения были выполнены три одинаковых эксперимента. В каждом опыте определялись значения частот, соответствующие максимуму функции спектральной плотности вдоль осей. Все полученные значения находились в интервале от 1257 Гц до 1288 Гц, что подтверждает стабильность результатов. Были проведены эксперименты для случая, когда ДУ в плоскости стола были повёрнуты на 45° относительно первоначального направления. Результаты экспериментов для всех характеристик хорошо совпадают с исходными. Экспериментально показана независимость результатов от длительности интервала нагружения и величины СКО, от точки расположения датчиков ускорения. Анализ результатов экспериментов [6,7]позволяет сделать вывод о том, что одномерные случайные процессы, описывающие колебания стола в направлении осей OX, OY, OZ, являются стационарными узкополосными гауссовскими процессами. Данный вывод согласуется с результатами теории случайных процессов о воздействии процесса типа «белый шум» на стационарную линейную систему [2].При воздействии широкополосного процесса пики получаемой спектральной плотности будут соответствовать собственным колебаниям системы. Отметим, что для полного описания вибрации стола, необходимо использовать понятие многомерного случайного процесса. Случайные одномерные процессы, определяемые в ходе экспериментов, являются его частными характеристиками. 2.3 Экспериментальная функция МСП конструкции ( ЕВ! необходимо в доступных границах дать описание конструкции, чтобы была ясна её сложная структура) Исследуемая конструкция (рис.2) представляет из себя сложную систему включающую значительное число взаимодействующих силовых элементов различного вида (тонкостенные оболочки, трехмерные массивные тела и т.д.), которые выполнены из различных материалов. Демпфирующие характеристики известны только для ограниченного числа материалов. Анализ поведения конструкции при различных видах внешнего воздействия с использование конечно-элементного подхода требует определения матрицы демпфирования, что в силу сложности конструкции представляется чрезвычайно трудным. Для определения демпфирующих свойств конструкции использовалась предложенная выше методика. Был выполнен ряд экспериментов по исследованию отклика конструкции на случайное воздействие. Конструкция своим основанием жестко крепилась к столу стенда. Виброизмерения выполнялись в ряде наиболее характерных точек конструкции, при различных ориентациях датчиков ускорений по отношению к координатным осям (направления координатных осей указаны на рис.2). Всего были выполнены эксперименты для получения МСП в 16 точках конструкции. На рис.2 показаны датчики, расположенные в точках 2,4,5. В точке 2 (зона стойки на днище внешней обечайки) датчик ориентирован вдоль оси OX, в точке 5 (зона расположения пружин на верху цилиндрической части внешней обечайки) ориентирован вдоль оси OZ, в точке 4 (зона днищ экранов на верху цилиндрической части внешней обечайки) ориентирован вдоль оси OZ. Контроль и управлениевыполняетсяДУ направленнымвдоль оси OZ. При подобном же расположении датчиков по точкам и по ориентации был также осуществлен эксперимент при условии, что контроль и управление вибрации стола осуществляется ДУ направленным вдоль оси OX.  Рис.2 Расположение на конструкции датчиков ускорений в точках 2,4,5, А- управляющий датчик Вид МСП случайного процесса нагружения полученной в эксперименте с ДУ установленном на рабочем столе и направленном вдоль оси OZв двойных логарифмических координатах показан на рис.3.Приведенные результаты использовались при задании характеристик внешнего воздействия при выполнении численных экспериментов.  Рис.3 МСП в двойных логарифмических координатах Результаты ряда натурныхэкспериментов по определению МСП конструкции в точках 2,4,5 представлены на рис.4,5.  Рис.4 Функции мощности спектральной плотности для точек 2, 4 и 5 при управлении по оси OZ  Рис.5 Функции мощности спектральной плотности для точек 2, 4 и 5 в направлении оси OY при управлении по оси OY Обработка и анализ результатов полученных при проведении экспериментов позволила в дальнейшем выбрать МСП наиболее подходящие для определения демпфирующих характеристик. 2.4 Оценка демпфирующих характеристик конструкции Для определения демпфирующих характеристик конструкции в соответствии с предложенной методикой был выполнен ряд виртуальных экспериментов с использованием МКЭ. При этом к конструкции прикладывалась случайная вибрация в жесткой заделке опорной плиты. Данная случайная вибрация имела МСП, показанную на рис.2. Интервал (5) изменения коэффициента  принимался равным[0, 0,1].Дискретные значения коэффициента(6) имели значения 0; 0,01; 0,05; 0,1. Указанный набор выбирался в соответствии с рекомендациями стандартов [8,9].В соответствии с выбранными значениями выполнялисьчисленные эксперименты. принимался равным[0, 0,1].Дискретные значения коэффициента(6) имели значения 0; 0,01; 0,05; 0,1. Указанный набор выбирался в соответствии с рекомендациями стандартов [8,9].В соответствии с выбранными значениями выполнялисьчисленные эксперименты.На рис.6 показаны для точки 2 (рис.2) расчётные значения МСП перегрузок в направлении оси OX при различных величинах коэффициента собственного трения. Вибрация задавалась в направлении оси OZ. На рисунке приведена полученная в эксперименте функция МСП.  Рис.6. Функции мощности спектральной плотности для точки 2 в направлении оси OX при управлении по оси OZ. На основе анализа полученных в предыдущих пунктах результатов пример, которых приведен на рис.6, была получена свертка  .Для данной функции с использованием процедуры lsqnonlinпакете MATLAB, в которой реализованы алгоритмы Гаусса-Ньютона и Левенберга-Марквардта [11,12], был найден минимум свертки. Данному минимуму соответствует решение задачи минимизации: искомый коэффициент собственного трения в конструкции .Для данной функции с использованием процедуры lsqnonlinпакете MATLAB, в которой реализованы алгоритмы Гаусса-Ньютона и Левенберга-Марквардта [11,12], был найден минимум свертки. Данному минимуму соответствует решение задачи минимизации: искомый коэффициент собственного трения в конструкции  . .Отметим, что значения величины  определенной с использованием экспериментальных данных для других точек конструкции отличались от указанной на величину не более 10%. определенной с использованием экспериментальных данных для других точек конструкции отличались от указанной на величину не более 10%.Заключение Предложена расчетно-экспериментальная методика определения демпфирующих свойств сложных многокомпонентных конструкций. Выполнена оценка демпфирующих свойств сложной конструкции, показавшая эффективность предлагаемой методики. Список литературы 1. Болотин В.В. Методы теории вероятностей и теории надёжности в расчётах сооружений, издание 2-е, переработанное и дополненное. М.: Стройиздат, 1981. 351 с. 2. Свешников А.А. Прикладные методы теории случайных функций, издание 2-е, переработанное и дополненное. М.: Главн. ред. физ.-мат. лит.изд-ва «Наука», 1968. 464 с. 3. Бате К. Вилсон Е. Численные методы анализа и метод конечных элементов. М. Стройиздат, 1982. 4. Вибрации в технике: спр. в 6 Т/ Ред. совет В.Н. Челомей (пред.). – М.: Машиностроение, 1981. – Т.6: Защита от вибраций и ударов/ Под ред. К.В. Фролова, 1981, 456 с. 5. Вибрации в технике: спр. в 6 Т/ Ред. совет В.Н. Челомей (пред.). – М.: Машиностроение, 1979. – Т.2: Колебания нелинейных механических систем/ Под ред. И.И. Блехмана, 1979, 351 с. 6. Берендеев Н.Н., Жидков А.В. Любимов А.К. Экспериментально-расчетная методика определения собственных частот конструкции. Вестник Нижегородского университета им. Н.И. Лобачевского. №1 .- Н.Новгород: изд. ННГУ им. Н.И. Лобачевского, 2010. С. 144-151. 7. Любимов А.К. Определение собственных частот конструкции с использованием трехмерного случайного воздействия: Доклады Х Всероссийского съезда по фундаментальным проблемам теоретической и прикладной механики // Вестник ННГУ. Сер. Механика. Н.Новгород: Изд-во Нижегородского госуниверситета. - 2011. - №4(2). - С.214-216. 8. ГОСТ Р 53190-2008 (МЭК 60088-2-81:2003) Испытания на удар с воспроизведением ударного спектра. 25 с. 9. ГОСТ 30630.1.8-2002 (МЭК 60068-2-57:1989) Методы испытания на стойкость к механическим внешним воздействующим факторам машин, приборов и других технических изделий: Испытания на воздействие вибрации с воспроизведением заданной акселерограммы процесса. 16 с. 10. MIL-STD-810F. ENVIRONMENTAL ENGINEERING CONSIDERATIONS AND LABORATORY TESTS.2000. 539 p. 11. Кетков Ю.Л., Кетков А.Ю., Шульц М.М. Matlab 7: программирование, численные методы. – СПб: БХВ-Петербург, 2005. – 752 с. 12. Каханер Д, Моулер К., Нэш С. Численные методы и программное обеспечение. – М.: Мир, 2001. – 575 с. |
