Физика Оптика. Определение длины волны излучения лазера по интерференционной картине полос равного наклона
 Скачать 149.41 Kb. Скачать 149.41 Kb.
|
 Министерство образования Российской Федерации Санкт-Петербургский государственный горный институт им. Г.В. Плеханова (технический университет)  Отчёт по лабораторной работе № 172По дисциплине: Физика(наименование учебной дисциплины согласно учебному плану) Тема: Определение длины волны излучения лазера по интерференционной картине полос равного наклонаВыполнил: студент гр. ОП-01 ______________ /Яикова Е.Н./ (подпись) (Ф.И.О.) ОЦЕНКА: _____________ Дата: __________________ ПРОВЕРИЛ:Руководитель: ____________ /Пучков А.М./(подпись) (Ф.И.О.) Санкт-Петербург 2002 год. Цель работы: определить длину волны излучения лазера по интерференционной картине полос равного наклона.Краткое теоретическое обоснование. Рассмотрим формирование интерференционной картины при отражении оптического излучения от плоскопараллельной пластины толщины d из стекла с показателем преломления n (рис. 1). Выделим волну (луч), падающую на верхнюю поверхность пластины под углом i . Отражение от верхней поверхности даёт волну 1. Преломлённая    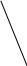 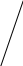  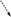   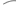                2 1 β n D C i B A d O i Рис. 1 в пластине под углом β волна доходит до нижней поверхности. В точке В происходит отражение и преломление волны. Преломленная волна нас далее не интересует. Отраженная волна возвращается к верхней грани и выходит, преломляясь в точке С ещё раз. Волны 1 и 2 когерентны, т.к. образовались в результате деления на части одного и того же волнового цуга, и между ними существует оптическая разность хода: ΔL = n2 l2 – n1 l1. Здесь l1 и l2 геометрические длины путей лучей 1 и 2, n1 и n2показатели преломления среды и пластинки, причем n2 = n, n1 = 1(воздух). Геометрические длины путей лучей l1 и l2 различны, начиная от точки О, после которой волны разделились, и до плоскости DC, после которой волны 1 и 2 идут параллельно в одной среде. l2 = OB + BC = 2OB = 2d /cos β ; l1 = OD = OC sin i ; OC = 2 AB = 2d tg β . Здесьd - толщина пластинки. Согласно закону преломления, sini = nsin β. Следовательно, l1 = 2d tg β n sin β = 2 dn sin2β/ cos β. Тогда для разности хода имеем: ΔL = 2dn/ cos β – 2dn sin2β/ cos β = 2dn cos β. Необходимо учесть, что при отражении на границе с оптически более плотной средой электромагнитная волна меняет скачком фазу на π . Поскольку в данном случае это относится к волне 1, оптическая разность хода уменьшится на λ/2: ΔL = 2dn cos β - λ/2. Когерентность излучения лазера позволяет с его помощью наблюдать интерференционные полосы при большой толщине плоскопараллельной пластины. Оптическая схема установки представлена на рис. 2. Лазер 1 даёт практически параллельный пучок света, из которого микрообъектив 2 формирует расходящийся пучок, освещающий стеклянную плоскопараллельную пластину 3. Отражённые от передней и задней поверхностей пластины волны интерферируют с образованием интерференционной картины на экране 4. 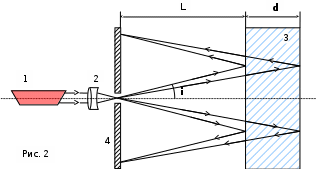 Выразим оптическую разность хода через угол падения: 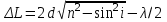 , ,Интерференционная картина имеет в этом случае вид концентрических тёмных и светлых колец. Каждое кольцо образовано интерферирующими волнами, падающими на пластину под близкими углами, отсюда их название – интерференционные полосы равного наклона. Условие возникновения тёмного кольца имеет вид 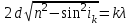 , (1) , (1)где k = 1, 2, …. – порядок интерференции. Порядок интерференции – это число, показывающее, во сколько раз длина волны излучения укладывается в оптической разности хода. В нашем случае углы падения малы, поэтому 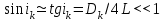 , (2) , (2)где Dk – диаметр тёмного кольца, L – расстояние от пластины до экрана. Условие (2) даёт возможность при разложении корня в ряд ограничиться двумя членами и преобразовать (1) к виду: 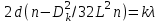 . (3) . (3)Соответственно, для тёмного кольца, отличающегося по порядку интерференции на величину Δk , будем иметь: 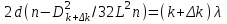 . (4) . (4)Совместное решение (3) и (4) даёт окончательную расчётную формулу для длины волны излучения лазера: 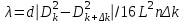 (5) (5)Для центра интерференционной картины i = 0, поэтому условие минимума (1) принимает вид: 2dn = kλ(6) что позволяет рассчитать порядок интерференции в центре интерференционной картины, если известны d, n, λ. В предлагаемой экспериментальной установке лучи света падают на пластину под некоторым углом ("косое" падение) (рис. 3). Поэтому, рассчитывая разность хода, необходимо учитывать смещение D0 центра интерференционной картины от центра отверстия в экране. Несложно убедиться, что в расчётной формуле (5) при этом появляется добавочное слагаемое, и она приобретает следующий вид: 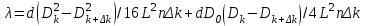 (7) (7)Используемая в работе плоскопараллельная пластина имеет параметры: d = 3 ±0,1 мм ; n = 1,51. Расстояние L измеряется линейкой с точностью до 5мм. 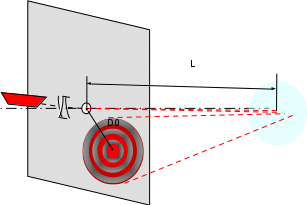 Рис.3 Расчет результатов эксперимента. L=570 мм D0=25 мм d=3±0,1 мм n=1,51 D1=37мм D2=59мм D3=75мм D4=86мм 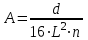 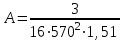 =0,0000003 =0,0000003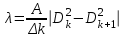 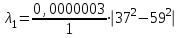 = 0,0006 мм = 0,0006 мм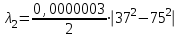 = 0,00063 мм = 0,00063 мм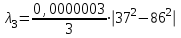 = 0,00061 мм = 0,00061 мм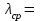 0,0006 мм 0,0006 ммРасчет погрешности  =0,017 =0,017Вывод: в данной лабораторной работе была измерена длина волны излучения лазера по интерференционной картине полос равного наклона. Полученная погрешность имеет небольшое значение, что говорит об отсутствии грубых ошибок при измерении и вычислении значение. |
