Гипербола. Определение Гиперболические функции задаются следующими формулами гиперболический синус
 Скачать 361.88 Kb. Скачать 361.88 Kb.
|
|
Определение Гиперболические функции задаются следующими формулами: гиперболический синус: 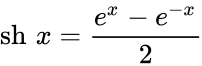 (в зарубежной литературе обозначается (в зарубежной литературе обозначается гиперболический косинус: 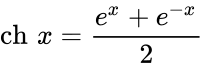 (в зарубежной литературе обозначается (в зарубежной литературе обозначается гиперболический тангенс: 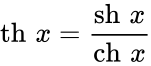 (в зарубежной литературе обозначается (в зарубежной литературе обозначается Иногда также определяются гиперболический котангенс: 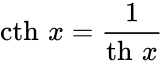 , ,гиперболические секанс и косеканс: 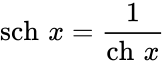 , ,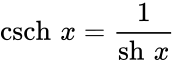 . .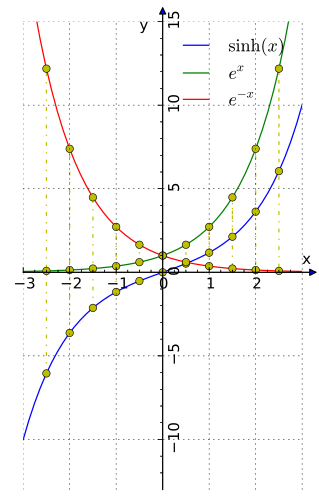 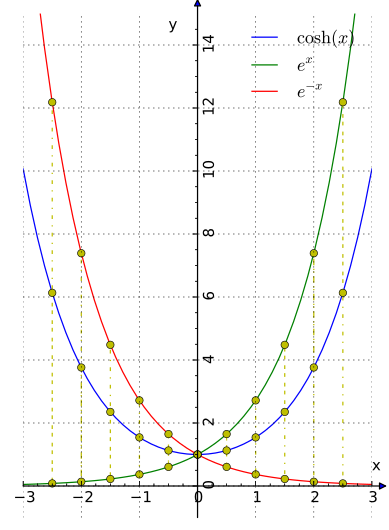 Геометрическое определение Ввиду соотношения ch2 t – sh2 t = 1 гиперболические функции дают параметрическое представление гиперболы 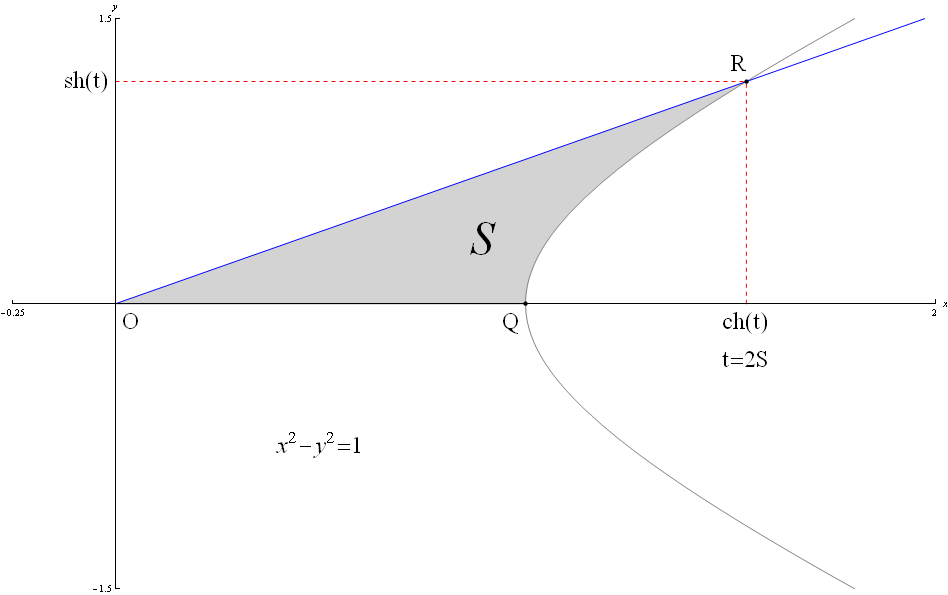 Свойства Связь с тригонометрическими функциями Гиперболические функции выражаются через тригонометрические функции от мнимого аргумента. Важные тождества ch2 t – sh2 t = 1 Чётность: Формулы сложения: Формулы двойного угла: 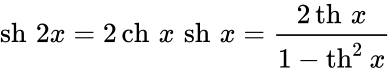 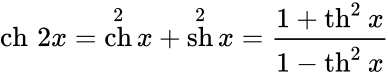 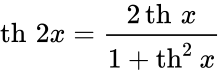 Производные: 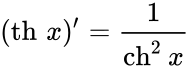 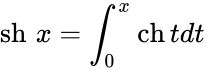 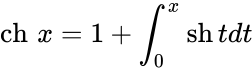 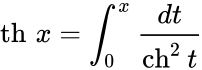 Интегралы: 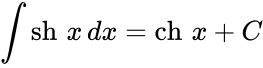 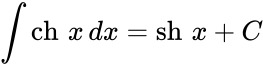 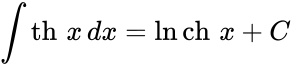 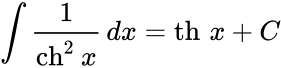 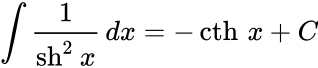 Разложение в степенные ряды 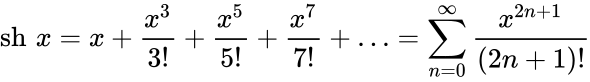 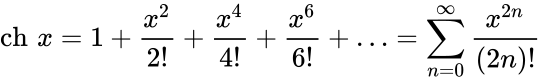 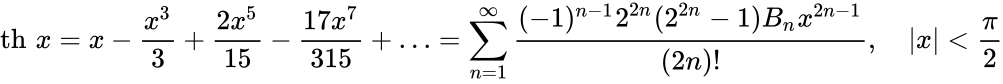 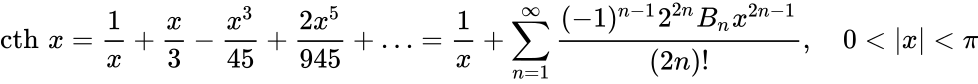 (Ряд Лорана) (Ряд Лорана)Здесь Аналитические свойств Гиперболический синус и гиперболический косинус аналитичны во всей комплексной плоскости, за исключением существенно особой точки на бесконечности. Гиперболический тангенс аналитичен везде, кроме полюсов в точках Обратные гиперболические функции Читаются ареа… (-синус и т. д.) — от лат. «area» — «площадь». 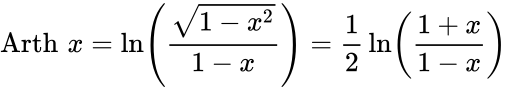 — обратный гиперболический тангенс — обратный гиперболический тангенс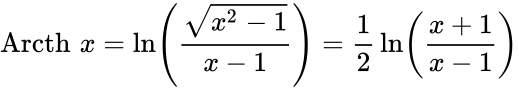 — обратный гиперболический котангенс — обратный гиперболический котангенс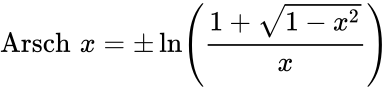 — обратный гиперболический секанс — обратный гиперболический секанс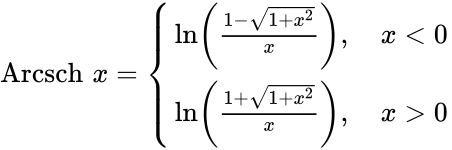 — обратный гиперболический косеканс — обратный гиперболический косекансЭти функции имеют следующее разложение в ряд: 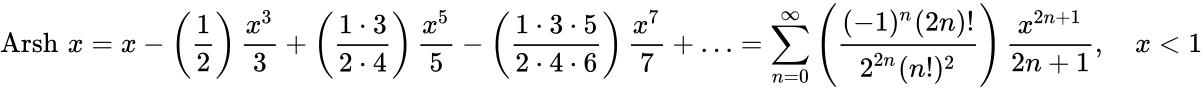 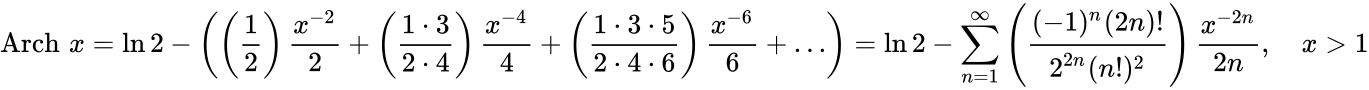 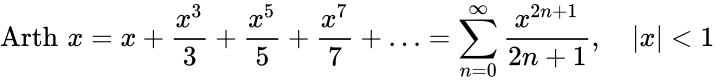 История Гиперболические функции были введены Винченцо Риккати (Vincenzo Riccati) в 1757 году («Opusculorum», том I). Он получил их из рассмотрения единичной гиперболы. Дальнейшее исследование свойств гиперболических функций было проведено Ламбертом. Риккати применял для гиперболических функций обозначения Применение Гиперболические функции часто встречаются при вычислении различных интегралов. Некоторые интегралы от рациональных функций и от функций, содержащих радикалы, довольно просто выполняются с помощью замен переменных с использованием гиперболических функций. Аналогично тому, как матрицы вида 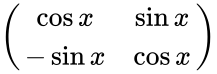 описывают повороты двумерного евклидова пространства, матрицы описывают повороты двумерного евклидова пространства, матрицы 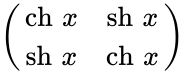 описывают повороты в простейшем двумерном пространстве Минковского. В связи с этим гиперболические функции часто встречаются в теории относительности. описывают повороты в простейшем двумерном пространстве Минковского. В связи с этим гиперболические функции часто встречаются в теории относительности.Однородная веревка или цепочка, свободно подвешенная за свои концы, приобретает форму графика функции |
