крен геодезия. КРЕН. Определение крена дымовой трубы
 Скачать 111.07 Kb. Скачать 111.07 Kb.
|
«Определение крена дымовой трубы»αАВ=52°52´52´´ Координаты точки А: ХА= 100.00 м; YА= 100.00 м. Журнал угловых и линейных измерений.
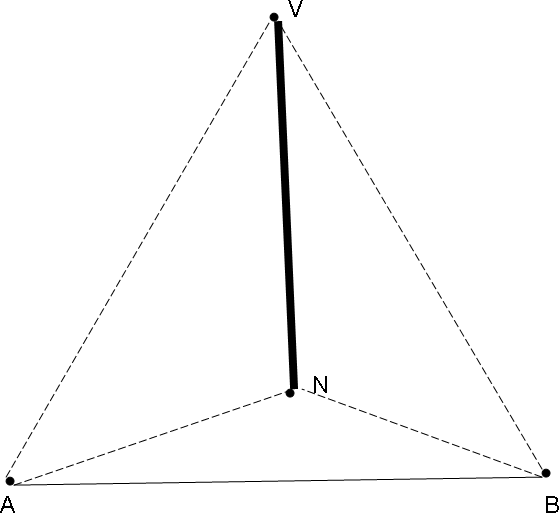 Рисунок 1. Рассмотрим треугольник ABN.Определяем углы треугольника ABN: ∠NAB=360º-297º46´45´´ = 62º13´15´´ ∠NBA=63º48´49´´ ∠ANB=180º-(62º13´15´´+ 63º48´49´´) = 180º-126º02´04´´ = 53º57´56´´ Зная углы в треугольнике и длину стороны, можно вычислить по теореме синусов стороны треугольника. Найдем стороны по теореме синусов:   BN = AB , BN = AB ,sin(BAN) sin (BNA)   AN = AB . AN = AB .sin(ABN) sin (BNA) BN  = =sin(62º13´15´´) 100,908  sin (53º57´56´´) BN  = =0,8847 100,908  0.8086 BN = 100,908 ⋅ 0,8847  0,8086 = 110,4047 м AN  = =sin(63º48´49´´) 100,908  sin (53º57´56´´) AN  = =0.8973 100,908  0.8086 AN = 100,908 ⋅ 0,8973  0,8086 = 111,9771 м Находим координаты точки В: 𝑥𝐵 = 𝑥𝐴 + 𝑑𝐴𝐵 · cos 𝛼𝐴𝐵 𝑦𝐵 = 𝑦𝐴 + 𝑑𝐴𝐵 · sin 𝛼𝐴𝐵 𝑥𝐵 = 100,00 + 100,908 · cos 14°14´14´´ 𝑦𝐵 = 100,00 + 100,908 · sin 14°14´14´´ 𝑥𝐵 = 197,809 м 𝑦𝐵 = 124,817 м По дирекционному углу линии АВ и углу NAB (рис.2) можно вычислить дирекционный угол линии AN. 𝛼𝐴𝑁 = 𝛼𝐴𝐵 − ∠𝑁𝐴𝐵 𝛼𝐴𝑁 = 52°52´52´´ − 62º13´15´´ = -9°20´23´´ Вычислив по теореме синусов расстояние AN и определив дирекционный угол 𝛼𝐴𝑁 по формулам прямой геодезической задачи находим координаты X и Y точки N. 𝑥𝑁 = 𝑥𝐴 + 𝑑𝐴𝑁 · cos 𝛼𝐴𝑁 𝑦𝑁 = 𝑦𝐴 + 𝑑𝐴𝑁 · sin 𝛼𝐴𝑁 𝑥𝑁 = 100,00 + 111,9771 · cos -9°20´23´´ 𝑦𝑁 = 100,00 + 111,9771 · sin -9°20´23´´ 𝑥𝑁 = 210,49м 𝑦𝑁 = 81,82 м Аналогично определяем координаты точки N eё вершины B треугольника ABN. 𝑥𝑁 = 𝑥𝐵 + 𝑑𝐵𝑁 · c𝑜𝑠 𝛼𝐵𝑁, 𝑦𝑁 = 𝑦𝐵 + 𝑑𝐵𝑁 · sin 𝛼𝐵𝑁 Где 𝛼𝐵𝐴 = 𝛼𝐴𝐵 + 180° = 52°52´52´´ + 180° = 232°52´52´´ 𝛼𝐵𝑁 = 𝛼𝐵𝐴 + ∠𝐴𝐵𝑁 = 232°52´52´´ + 63°48´49´´ = 296°41´41´´ 𝑥𝑁 = 197,809 + 110,4047 · c𝑜𝑠 296°41´41´´ 𝑦𝑁 = 124,817 + 110,4047 · sin 296°41´41´´ 𝑥𝑁 = 247,41 м 𝑦𝑁 = 26,18 м Находим среднее значение координат X и Y точки N. 𝑋𝑁 = 𝑌𝑁 = 210,49 + 247,41  = 228,95 м = 228,95 м2 81,82 + 26,18  = 54 м = 54 м2 Рассмотрим треугольник ABV.Определяем углы треугольника ABV: ∠VAB=360º-296º20´57´´ = 63º39´03´´ ∠VBA= 62º28´38´´ ∠AVB=180º-(63º39´03´´+ 62º28´38´´) = 180º-126º07´41´´ = 53º52´19´´ Зная углы в треугольнике и длину стороны, можно вычислить по теореме синусов стороны треугольника. Найдем стороны по теореме синусов:   BV = AB , BV = AB ,sin(BAV) sin (BVA)   AV = AB . AV = AB .sin(ABV) sin (BVA) BV  = =sin(63º39´03´´) 100,908  sin (53º52´19´´) BV  = =0,8961 100,908  0,8077 BV = 100,908 ⋅ 0,8961  0,8077 = 111,9520 м AV  = =sin(62º28´38´´) 100,908  sin (53º52´19´´) AV  = =0.8868 100,908  0.8077 AV = 100,908 ⋅ 0,8868  0,8077 = 110,7901 м По дирекционному углу линии АВ и углу VAB (рис.2) можно вычислить дирекционный угол линии AV. 𝛼𝐴𝑉 = 𝛼𝐴𝐵 − ∠𝑉𝐴𝐵 𝛼𝐴𝑁 = 52°52´52´´ − 63º39´03´´= -10°46´11´´ Вычислив по теореме синусов расстояние AV и определив дирекционный угол 𝛼𝐴𝑉 по формулам прямой геодезической задачи находим координаты X и Y точки N. 𝑥𝑉 = 𝑥𝐴 + 𝑑𝐴𝑉 · cos 𝛼𝐴𝑉 𝑦𝑉 = 𝑦𝐴 + 𝑑𝐴𝑉 · sin 𝛼𝐴𝑉 𝑥𝑉 = 100,00 + 110,7901 · cos -10°46´11´´ 𝑦𝑉 = 100,00 + 110,7901 · sin -10°46´11´´ 𝑥𝑉 = 208,84 м 𝑦𝑉 = 79,30 м Аналогично определяем координаты точки V eё вершины B треугольника ABV. 𝑥𝑉 = 𝑥𝐵 + 𝑑𝐵𝑉 · c𝑜𝑠 𝛼𝐵𝑉, 𝑦𝑉 = 𝑦𝐵 + 𝑑𝐵𝑉 · sin 𝛼𝐵𝑉 Где 𝛼𝐵𝐴 = 𝛼𝐴𝐵 + 180° = 52°52´52´´ + 180° = 232°52´52´´ 𝛼𝐵𝑉 = 𝛼𝐵𝐴 + ∠𝐴𝐵𝑉 = 232°52´52´´ + 62º28´38´´ = 295°21´30´´ 𝑥𝑉 = 197,809 + 111,9520 · c𝑜𝑠 295°21´30´´ 𝑦𝑉 = 124,817 + 111,9520 · sin 295°21´30´´ 𝑥𝑉 = 245,75 м 𝑦𝑉 = 23,65 м Находим среднее значение координат X и Y точки V. 𝑋𝑉 = 𝑌𝑉 = 208,84 + 245,75  = 227,29 м = 227,29 м2 79,30 + 23,65  = 51,47 м = 51,47 м2 По средним координатам точек N и V определяем угловую и линейную величины крена дымовой трубы:  𝑞𝑉𝑁 = √(𝑥𝑉 − 𝑥𝑁)2 + (𝑦𝑉 − 𝑦𝑁)2  𝑞𝑉𝑁 = √(227,29 − 228,95)2 + (51,47 − 54)2 = 4,19 𝑦𝑉 − 𝑦𝑁 𝑡𝑔𝜃 = 𝑡𝑔𝜃 =  𝑥𝑉 − 𝑥𝑁 51,47 − 54  227,29 − 228,95 = 1.5  | |||||||||||||||||||||||||
