Курсовая темы Трофимовские числа. Определение момента инерции твердого тела методом трифилярного подвеса
 Скачать 94 Kb. Скачать 94 Kb.
|
|
Министерство образования и науки Российской Федерации Волгоградский государственный технический университет Институт архитектуры и строительства Кафедра физики ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТВЕРДОГО ТЕЛА МЕТОДОМ ТРИФИЛЯРНОГО ПОДВЕСА Методические указания к лабораторной работе № 6 Волгоград 2018УДК 378.141.001 Определение момента инерции твердого тела методом трифилярного подвеса: Методические указания к лабораторной работе №6 / Сост. Л.А. Васильева; ВолгГАСА. – Волгоград, 2002. – 8 с. Целью работы является определение момента инерции твердого тела в форме диска методом трифилярного подвеса и проверка теоремы Штейнера. В методических указаниях дана краткая теория, подробно описан метод измерений и постановка задачи, приведен порядок выполнения работы, правила техники безопасности и контрольные вопросы. Для студентов всех специальностей. Ил. 1. Табл. 1. Библиогр. 4 назв. © Волгоградская государственная архитектурно-строительная академия, 2002 © Составление Васильева Л.А. Цель работы - определение момента инерции твердого тела, проверка теоремы Штейнера. Приборы и принадлежности: трифилярный подвес, электронный секундомер, тело для измерения момента инерции в виде разрезанного на две части диска. 1. ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕМоментом инерции материальной точки называется произведение массы точки на квадрат расстояния до оси вращения J=mr2. Момент инерции системы материальных точек равен сумме моментов инерции всех точек системы относительно оси вращения Твердое тело можно мысленно разделить на элементарные массы Δmi, находящиеся на расстоянии ri от оси вращения. Момент инерции твердого тела равен сумме моментов инерции всех элементарных масс что, по определению, при m0представляет собой интеграл J=∫r2dm. Интеграл легко вычисляется для однородных тел симметричной формы относительно оси, проходящей через центр инерции. Например, для диска радиусом Rи массой m момент инерции относительно оси, проходящей через центр инерции перпендикулярно плоскости диска, равен J=mR2/2. Момент инерции тела зависит от выбора оси вращения. Если известен момент инерции тела относительно оси, проходящей через центр инерции Jc, то можно найти момент инерции относительно любой параллельной оси Jo, если применить теорему Штейнера. Согласно теореме момент инерции тела относительно произвольной оси Jo равен сумме момента инерции относительно параллельной оси, проходящей через центр инерции Jc , и произведения массы тела m на квадрат расстояния между осями d Jo=Jc+md2. 2. МЕТОД ИЗМЕРЕНИЙ Н 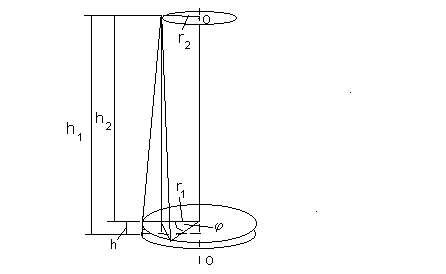 а практике момент инерции тела можно определить методом трифилярного подвеса, который представляет собой круглую платформу радиусом r1и массой m, подвешенную к неподвижному диску радиусом r2 на трех симметрично расположенных нитях длиной l(см. рисунок). Трифилярный подвес Если повернуть платформу вокруг вертикальной оси ОО на угол , то возникает момент сил, обусловленный суммарным действием силы тяжести и натяжения нити и стремящийся вернуть платформу в положение равновесия. Платформа начнет совершать крутильные колебания вокруг оси ОО. Полная механическая энергия платформы E складывается из кинетической энергии J2/2 и потенциальной mgh J2/2 + mgh = E , (1) где h – высота, на которую приподнимается центр тяжести платформы при повороте от положения равновесия, у Выражение для высоты, на которую приподнимается центр тяжести платформы, получим, анализируя рисунок. h=h1 – h2=(h12-h22)/(h1+h2), h12=l2-(r1-r2)2, h22= l2-(r12+r22-2r1r2cos). Получаем выражение h=2r1r2(1 - cos)/(h1+h2). Заменим 1 - cos =2sin2(/2)2/2 . Здесь учли, что для малых углов sin(/2)/2 . Кроме того, для (r1-r2)l можно положить, что h1+h22l, тогда h = r1r22 /2l. (2) Подставив (2) в (1), получаемJ2/2 + mgr1r22/2l= E. Если пренебречь потерями на трение, то полная механическая энергия системы не изменяется, то есть E=const. Тогда, продифференцировав это выражение по времени, сократив на и поделив на J, получим дифференциальное уравнение движения системы Можно убедиться непосредственной подстановкой, что решение этого уравнения имеет вид гармонического колебания = о sin (o t+ o), (4) циклическая частота которого а период колебаний Отсюда можно получить формулу для определения момента инерции системы (7) Если на платформе находится тело, то в формуле (7) в этом случае под m понимается суммарная масса тела и платформы, а под J – суммарный момент инерции. 3. ПОСТАНОВКА ЗАДАЧИ Цель работы состоит в определении момента инерции тела и экспериментальной проверке теоремы Штейнера на основе исследования зависимости момента инерции тела от расстояния до оси вращения. В дальнейшем обозначим массу платформы радиусом r1 через m1, а массу тела, имеющего вид диска радиусом r, разделенного на две равные части, через m. Половинки диска располагают на платформе симметрично относительно оси вращения во избежание перекоса платформы. Момент инерции диска относительно оси вращения ОО по теореме Штейнера равен Jd = mr2/2+md2. (8) Чтобы найти момент инерции системы платформа-диск, нужно к моменту инерции платформы J1=m1r12/2 прибавить момент инерции диска Jd J= m1r12/2+ mr2/2+md2. (9) Момент инерции системы платформа-диск можно найти экспериментально, если измерить период колебаний для разных значений d и воспользоваться формулой (7), которая с учетом массы диска примет вид Величина момента инерции тела определяется как разность Jd= J -J1 . (11) Экспериментальное значение J1определяют, измерив период колебаний пустой платформы и произведя расчет по формуле (10) с учетом, что в этом случае масса тела m=0. Вращательный импульс, необходимый для начала крутильных колебаний, сообщается платформе путем поворота верхнего диска с помощью пружинотолкателя. Этим достигается почти полное отсутствие других, не крутильных, колебаний, наличие которых затрудняет измерения. 4. ПОРЯДОК ВЫПОЛНЕНИЯ 1. Включить электронный секундомер, ознакомиться с его работой и индикацией. С помощью пружинотолкателя возбудить крутильные колебания пустой платформы и измерить секундомером время 20 полных колебаний t. Найти период колебаний T=t/20. По формуле (10) определить момент инерции пустой платформы J1с учетом, что m=0. 2. Поставить на платформу диск так, чтобы центр диска совпадал с центром платформы. С помощью пружинотолкателя возбудить крутильные колебания и измерить секундомером время 20 полных колебаний t. Найти период колебаний T=t/20. По формуле (10) определить момент инерции системы платформа-тело и по формуле (11) – момент инерции тела. Результаты занести в таблицу. 3. Сместить в противоположных направлениях половинки диска на расстояние d=1смот оси вращения и повторить измерения предыдущего пункта. Проделать аналогичные измерения для d=2 см, 3 см, 4 сми5 см.. 4. По формулам (8) и (9) рассчитать теоретические значения момента инерции тела и системы платформа-тело. Результаты занести в таблицу. 5. По данным таблицы построить график зависимости момента инерции тела от квадрата расстояния до оси вращения Jd=f(d2) для экспериментальных и теоретических значений. 6. Для одного из значений сравнить экспериментальную величину Jd с теоретической Jdтеори найти относительную погрешность результатов по формуле 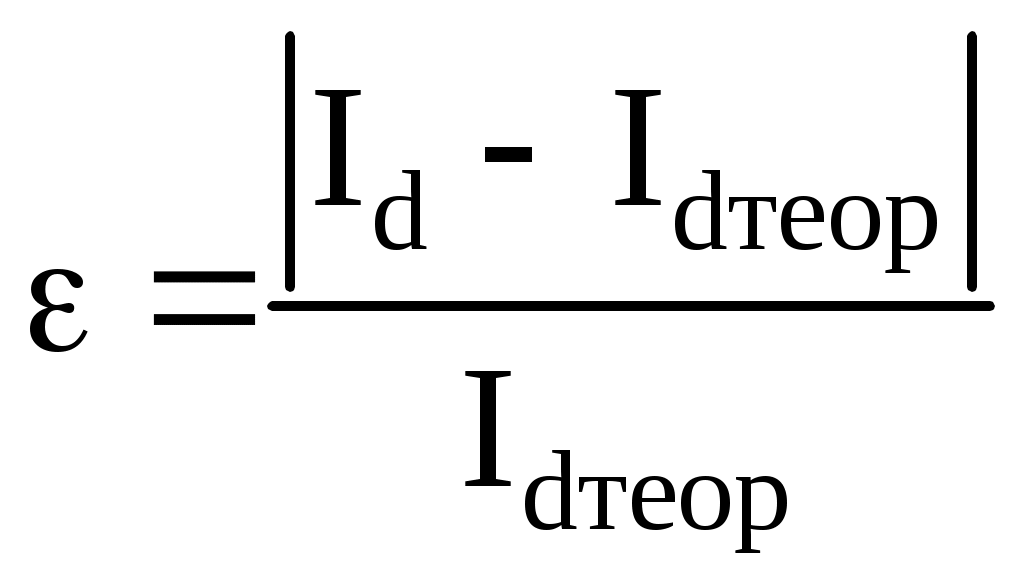 100 %. 100 %.Таблица
ТЕХНИКА БЕЗОПАСНОСТИ В работе для измерения времени используется электронный секундомер, питание которого осуществляется от сети переменного тока напряжением 220 В. При работе с электронным секундомером необходимо соблюдать правила техники безопасности работы с электроприборами. Сначала секундомер включается в розетку, затем – тумблер «сеть» на панели прибора. Выключение производится в обратном порядке. При наличии неисправности обратитесь к преподавателю или лаборанту. Не забудьте выключить установку после измерений. КОНТРОЛЬНЫЕ ВОПРОСЫ Что называется моментом инерции тела относительно оси? Сформулировать теорему Штейнера. В чем состоит метод измерения момента инерции тела с помощью трифилярного подвеса ? Какова природа сил, вынуждающих систему совершать крутильные колебания? Какие превращения энергии происходят при крутильных колебаниях? При каких условиях крутильные колебания системы можно считать гармоническими? Дать вывод формулы (7). Библиографический списокТрофимова Т.И. Курс физики. Учебник для студентов вузов. М.: Высшая школа, 1999. Каленков С.Г. Практикум по физике. Механика. Учебное пособие для студентов вузов/ С.Г. Каленков., Г.И. Соломахо; под ред. А.Д. Гладуна. М.: Высш. шк., 1990. Детлаф А.А. Курс физики/ А.А. Детлаф, Б.М. Яворский. М.: Наука, 1999 Лабораторные работы по механике/ Под ред. С.Д. Ханина. СПб: Изд. РГПУ им. А.И. Герцена, 2000. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
