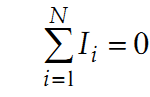|
|
ЛР 3.3. Определение неизвестных сопротивлений при помощи мостовой схемы
Отчёт по лабораторной работе 3.3.
По дисциплине: Физика
(наименование учебной дисциплины согласно учебному плану)
Тема: Определение неизвестных сопротивлений при помощи мостовой схемы
Выполнил: студент гр. ГГ-13-1 ___________ Куприянов В.О.
(подпись) (Ф.И.О.)
Дата: __________________
ПРОВЕРИЛ:
Доцент: ____________ Дьяконов К.В.
(подпись) (Ф.И.О.)
г. Иркутск, 2022 год
Цель работы: Изучение законов постоянного тока
В проводниках существуют свободные носители электрического заряда – электроны. Под действием электрического поля, которое можно создать в проводнике, возникает непрерывное упорядоченное движение электронов.
Такое движение называется электрическим током. За направление электрического тока принято направление движения свободных положительных зарядов.
Количественной мерой электрического тока служит сила тока I. Это скалярная физическая величина, которая определяет количество электричества, проходящего через поперечное сечение проводника за единицу времени:
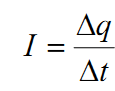
Силы неэлектростатического происхождения, действующие на свободные носители заряда со стороны источников тока, называются сторонними силами. При перемещении электрических зарядов по цепи постоянного тока сторонние силы, действующие внутри источников тока, совершают работу.
Электродвижущей силой источника (ЭДС) называется физическая величина, равная работе сторонних сил при перемещении заряда q от отрицательного полюса источника тока к положительному полюсу, отнесённая к величине этого заряда. ЭДС и в системе СИ измеряется в вольтах (В):
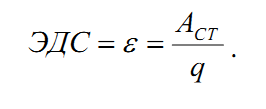
Цепь постоянного тока можно разбить на участки постоянного тока, на которых не действуют сторонние силы, то есть участки, не содержащие источников тока. Эти участки называются однородными. Участки, включающие источники тока, называются неоднородными.
Немецкий физик Г.Ом в 1826 г. экспериментально установил, что сила тока I, текущего по однородному проводнику (то есть проводнику, в котором не действуют сторонние силы), пропорциональна напряжению на концах проводника: 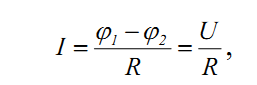
Закон Ома для замкнутой цепи: сила тока в электрической цепи прямо пропорциональна ЭДС и обратно пропорциональна сумме сопротивлений внешней и внутренней цепи:
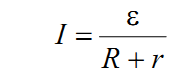
где R – внешнее сопротивление цепи; r – внутреннее сопротивление источника тока. Сопротивление однородного проводника:
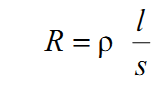
где 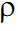 – удельное сопротивление проводника, Ом∙м; – удельное сопротивление проводника, Ом∙м; 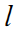 – длина проводника; s –площадь поперечного сечения. Большинство электрических цепей содержат комбинации последовательно или параллельно включённых сопротивлений. – длина проводника; s –площадь поперечного сечения. Большинство электрических цепей содержат комбинации последовательно или параллельно включённых сопротивлений.
Сопротивление последовательно соединенных проводников:
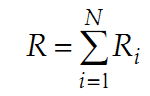
При параллельном соединении сопротивлений 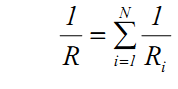
Для расчёта более сложных цепей существует способ, основанный на применении правил
Кирхгофа.
Первое правило Кирхгофа (правило для узла) – алгебраическая сумма всех N токов, сходящихся в узле, равна нулю. Узел-точка разветвления проводников
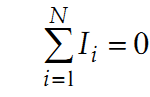
Второе правило Кирхгофа (правило для контура) – алгебраическая сумма падений напряжений, подсчитанных вдоль любого замкнутого контура, равна алгебраической сумме ЭДС источников, включенных в контур:
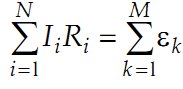
Для точного определения сопротивлений используют метод сравнения сопротивлений, не требующий измерения тока и напряжения. Этот метод осуществляется по схеме моста
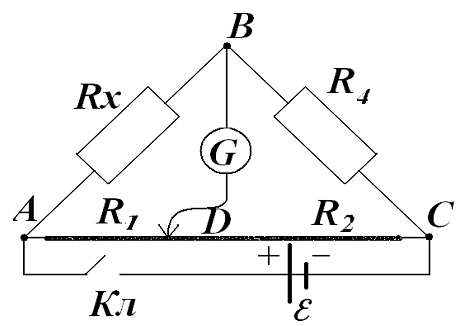
Электрическая мостовая схема (мост Уитстона) служит для определения электрического
сопротивления. Четыре сопротивления R1, R2, RХ, R4 составляют замкнутый
четырёхугольник АВСD. Противолежащие вершины четырёхугольника соединяются
диагоналями. В одну диагона, между точками С и D, подключается гальванометр G,
в другую – батарея 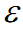 через ключ Кл. через ключ Кл.
Если участок последовательно включённых сопротивлений R1 и R2 заменяют прямым
однородным проводом, натянутым вдоль линейки, то такой мост называется реохордным.
Вдоль реохорда перемещается подвижной контакт D и сопротивления R1 и R2
изменяются пропорционально длине проволоки из формулы сопротивления однородного проводника. Положение движка D реохорда можно подобрать таким образом, чтобы ток в гальванометре G, включённом в диагональ моста, был равен нулю.
Это возможно тогда, когда потенциалы в точках В и D окажутся равными. При отсутствии тока
через гальванометр по первому правилу Кирхгофа можно записать: I1 = I2; IХ = I4. Так как
потенциалы точек В и D равны, значения падения напряжения на участках АВ и АD и
участках ВС и DС тоже будут равны; т.е.IхRх=I4R4. Измерительный мост в этом случае
оказывается сбалансированным. Полученные равенства разделим почленно и, принимая
во внимание, что I1= I2 а IХ = I4, получим:
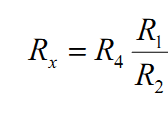
Таким образом, зная сопротивление одного проводника, например, R4 и отношение
сопротивлений двух других проводников, можно определить сопротивление
проводника. Заменяя сопротивления R1 и R2 длинами плеч L1 и L2, получим рабочую
формулу для определения неизвестного сопротивления:
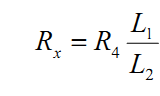
Выполнения работы
1. Ознакомился с работой мостовой схемы на виртуальной лабораторной установке: включение/выключение, работа реохорда и гальванометра, подключение сопротивлений,
изменение значений R4.
2. Выполнил пробные измерения, добиваясь нулевого отклонения стрелки гальванометра
G:
а) подбором R4 при различных фиксированных значениях L1/L2;
б) подбором соотношения плеч L1/L2 при различных фиксированных значениях
сопротивления R4.
3. Установил движок реохорда D на середину реохорда, а значение R4 на магазине
сопротивлений вывел на ноль.
4. Подключил к установке первое неизвестное сопротивление Rх1 и замкнул ключ К.
5. Изменяя сопротивления R4, добился минимального (нулевого) отклонения стрелки
гальванометра G при равном отношении плеч реохорда L1 и L2 (L1/L2=50/50).
6. Отсчитал и записал длину плеч реохорда L1 и L2, а также значение R4 в таблицу
результатов измерений.
7. Увеличил сопротивление магазина R4 на 20 % больше, чем было в п. 6 и, изменяя
отношение плеч реохорда L1 и L2, добиться того, чтобы отклонение стрелки гальванометра G
от нуля было наименьшим.
8. Данные записал в таблицу результатов измерений.
9. Уменьшил сопротивление магазина R4 на 20 % меньше, чем было в п. 6 и, изменяя
отношение плеч реохорда L1 и L2, добиться того, чтобы отклонение стрелки гальванометра G
от нуля было наименьшим.
10. Значение R4 и длину плеч реохорда L1 и L2 записал в таблицу результатов измерений.
11. Заменил неизвестное сопротивление Rх1 на неизвестное сопротивление Rх2 и повторил
измерения, следуя пп. 3-9. Записал результаты в таблицу.
12. Заменил неизвестное сопротивление Rх3 на последовательно соединённые неизвестные
сопротивления Rх1, и Rх2 и повторить измерения, следуя пп. 3-9. Результаты записал в таблицу.
13. Повторил измерения по пп. 3-9 для Rх4 (параллельно соединённых неизвестных
сопротивлений Rх1, и Rх2). Полученные результаты записал в таблицу.
14. Нашёл по результатам каждого опыта значения неизвестных сопротивлений RХ1, и RХ2, а
также их общее сопротивление при последовательном RХ3 и параллельном RХ4 соединениях,
их средние значения 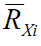 . .
Таблица измерений и вычислений
Измеряемые
сопротивления
|
Опыт
|
R4, Ом
|
L1, см
|
L2, см
|
RХi, Ом
|
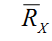 ,Ом ,Ом
|
Неизвестное
сопротивление RХ1
|
1
|
147,5
|
50
|
50
|
147,5
|
147,5
|
2
|
177,0
|
45,5
|
54,5
|
147,8
|
3
|
118,0
|
55,5
|
44,5
|
147,1
|
Неизвестное
сопротивление RХ2
|
1
|
253,0
|
50
|
50
|
253,0
|
252,9
|
2
|
303,3
|
45,5
|
54,5
|
253,2
|
3
|
202,4
|
55,5
|
44,5
|
252,4
|
Последовательное
соединение
сопротивлений RХ3
|
1
|
405,5
|
50
|
50
|
405,5
|
405,6
|
2
|
486,8
|
45,5
|
54,5
|
406,4
|
3
|
324,6
|
55,5
|
44,5
|
404,8
|
Параллельное
соединение
сопротивлений RХ4
|
1
|
95,5
|
50
|
50
|
95,5
|
95,5
|
2
|
114,6
|
45,5
|
54,5
|
95,7
|
3
|
76,4
|
55,5
|
44,5
|
95,3
|
15. Оценил погрешности измерений.
Формулы погрешностей косвенных измерений:
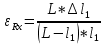 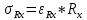 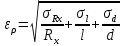 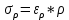
Исходные данные:
l1 = 0,455 (м) l2 = 0,545 (м) R =177,0 (Oм)
Вычисления:
Rx=(0,455*177,0)/0,545=147,8 Ом
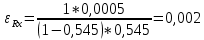
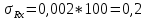
Результат вычислений:
Rx1=147,5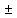 0,2 Ом. 0,2 Ом.
Rx2=252,9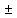 0,2 Ом. 0,2 Ом.
Rx,послед =405,6 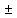 0,2 Ом 0,2 Ом
Rx,парал = 95,5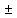 0,2 Ом 0,2 Ом
Вывод: при выполнении данной работы познакомился с методом расчета параметров
электрической цепи, основанном на использовании мостовых схем, нашел неизвестное
сопротивление при помощи моста.
Контрольные вопросы.
1. Непрерывное упорядоченное движение электронов называется электрическим током.
За направление электрического тока принято направление движения свободных
положительных зарядов. Количественной мерой электрического тока служит сила тока I.
Это скалярная физическая величина, которая определяет количество электричества,
проходящего через поперечное сечение проводника за единицу времени:
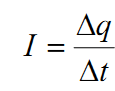
2. Силы неэлектростатического происхождения, действующие на свободные носители
заряда со стороны источников тока, называются сторонними силами. При перемещении
электрических зарядов по цепи постоянного тока сторонние силы, действующие внутри
источников тока, совершают работу.
3. Потенциалом электростатического поля называют отношение потенциальной энергии
заряда в поле к этому заряду.
Согласно данному определению потенциал равен:
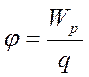
Подобно потенциальной энергии, значение потенциала в данной точке зависит от выбора
нулевого уровня для отсчета потенциала. Практическое значение имеет не сам потенциал в точке, а изменение потенциала, которое не зависит от выбора нулевого уровня отсчета потенциала.
Так как потенциальная энергия Wp = qφ, то работа равна:
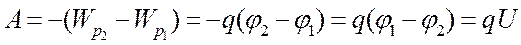
Величина 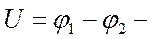 разность потенциалов. Разность потенциалов, т. е. разность значений потенциала в начальной и конечной точках траектории. разность потенциалов. Разность потенциалов, т. е. разность значений потенциала в начальной и конечной точках траектории.
Разность потенциалов называют также напряжением.
4. R= R1 + R2 + R3
5. R= R1* R2
R1 + R2
6. Немецкий физик Г.Ом в 1826 г. экспериментально установил, что сила тока I, текущего по однородному проводнику (то есть проводнику, в котором не действуют сторонние силы), пропорциональна напряжению на концах проводника и обратно пропорциональна сопротивлению проводника:
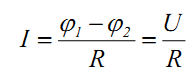 , где , где 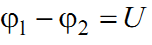 – напряжение на участке цепи; R – его сопротивление, – напряжение на участке цепи; R – его сопротивление,
Ом.
7. Цепь постоянного тока можно разбить на участки, на которых не действуют сторонние силы, то есть участки, не содержащие источников тока. Эти участки называются однородными. Участки,
включающие источники тока, называются неоднородными участками цепи.
8. Закон Ома для замкнутой цепи: сила тока в электрической цепи прямо пропорциональна ЭДС и обратно пропорциональна сумме сопротивлений внешней и внутренней цепи:
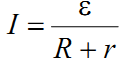
9. Первое правило Кирхгофа (правило для узла) – алгебраическая сумма всех N токов,
сходящихся в узле, равна нулю. Узел-точка разветвления проводников
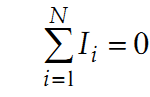
Второе правило Кирхгофа (правило для контура) – алгебраическая сумма падений напряжений, подсчитанных вдоль любого замкнутого контура, равна алгебраической сумме ЭДС источников, включенных в контур:
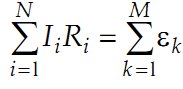
|
| |
|
|
 Скачать 104.87 Kb.
Скачать 104.87 Kb.
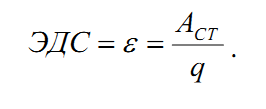
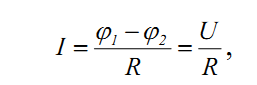
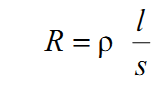

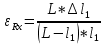
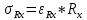
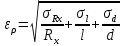
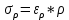
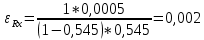
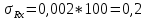
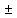 0,2 Ом.
0,2 Ом.