лекция 10. Определение веса поезда условию затяжного подъема. 20171025 1250 Поделись
 Скачать 65.92 Kb.
|
|
Определение веса поезда условию затяжного подъема.  2017-10-25 1250Поделись 5 6 7 8 9 10 11 В последующих лекциях, рассмотрев характеристики электроподвижного состава и автономных локомотивов, мы будем оперировать понятием расчетной (длительной) силы тяги локомотива. Немного упрощая, в данный момент времени можно дать такое определение: расчетная (длительная) сила тяги – это максимально возможное тяговое усилие реализуемое локомотивом бесконечно длительное время. Как правило, длительная сила тяги ограничена по условиям нагревания элементов тягового привода локомотива. Расчетной силе тяги соответствует расчетная скорость движения локомотива на номинальной позиции. Одним из важнейших понятий в теории тяги поездов является понятие затяжного подъема. Затяжным, называется такой подъем, в конце которого скорость движения поезда становится равной расчетной. Т.е. при движении по затяжному подъему локомотивом будет реализовываться расчетное значение силы тяги. Как правило, при подготовке к тяговым расчетам, нам неизвестно с какой скоростью поезд подойдет к затяжному подъему. Поэтому предполагаем худший случай, когда перед затяжным подъемом поезд не успел разогнаться и въезжает со скоростью равной расчетной скорости движения. Для того, чтобы не вызвать опасных режимов работы оборудования локомотива его скорость (v) должна оставаться равной расчетной (vp) и не снижаться ниже этой величины, т.е.  .Следовательно, ускорение (замедление) поезда равно 0 ( 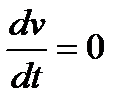 ).При выводе основного уравнения движения мы использовали следующую промежуточную его интерпретацию:  .Так как в режиме тяги тормоза поезда не применяются, а ускорение равно нулю получим: 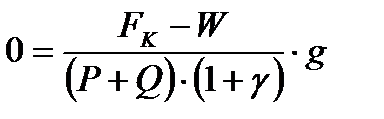 .С учетом того, что сила тяги и скорость равны расчетной, получим следующее выражение для определения веса поезда по затяжному подъему: 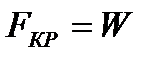 ;где FКР – расчетная сила тяги локомотивов; W – полное сопротивление движению поезда. С другой стороны, полное сопротивление движению поезда складывается из полного сопротивления движению локомотива (W/) и полного сопротивления движению состава (W//). 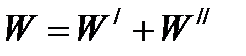 .В свою очередь полное сопротивление движению локомотива (W/) состоит из основного сопротивления движению ( 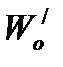 ) и сопротивления движению от затяжного подъема (  ). Сопротивление движению состава (W//) также состоит из основного сопротивления движению ( 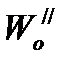 ) и сопротивления движению от затяжного подъема (  ). 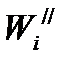.Абсолютные значения сил сопротивления движения локомотива и состава выражаются через их удельные величины:  ; ;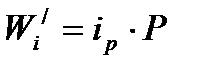 ; ;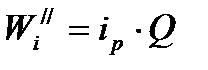где P, Q - вес локомотива и состава соответственно (т);  ,  - основное удельное сопротивление движению локомотива и состава соответственно (кгс/т); ip – величина расчетного (затяжного) подъема о/оо.Более подробно основное и дополнительное сопротивления движению будут рассмотрены отдельно. Подставив полученные слагаемые в одно уравнение получим следующее соотношение: 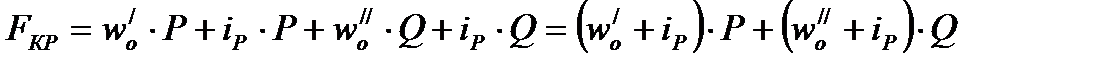 .Преобразуя данное выражение относительно веса состава, получим конечную формулу для определения веса состава по затяжному подъему: 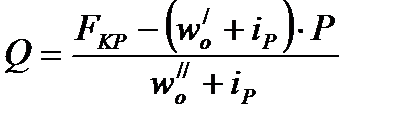 .Полученное соотношение позволяет определять допустимый вес состава без учета запаса кинетической энергии поезда. В последующих лекциях, рассмотрев характеристики электроподвижного состава и автономных локомотивов, мы будем оперировать понятием расчетной (длительной) силы тяги локомотива. Немного упрощая, в данный момент времени можно дать такое определение: расчетная (длительная) сила тяги – это максимально возможное тяговое усилие реализуемое локомотивом бесконечно длительное время. Как правило, длительная сила тяги ограничена по условиям нагревания элементов тягового привода локомотива. Расчетной силе тяги соответствует расчетная скорость движения локомотива на номинальной позиции. Одним из важнейших понятий в теории тяги поездов является понятие затяжного подъема. Затяжным, называется такой подъем, в конце которого скорость движения поезда становится равной расчетной. Т.е. при движении по затяжному подъему локомотивом будет реализовываться расчетное значение силы тяги. Как правило, при подготовке к тяговым расчетам, нам неизвестно с какой скоростью поезд подойдет к затяжному подъему. Поэтому предполагаем худший случай, когда перед затяжным подъемом поезд не успел разогнаться и въезжает со скоростью равной расчетной скорости движения. Для того, чтобы не вызвать опасных режимов работы оборудования локомотива его скорость (v) должна оставаться равной расчетной (vp) и не снижаться ниже этой величины, т.е. .Следовательно, ускорение (замедление) поезда равно 0 ( 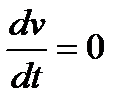).При выводе основного уравнения движения мы использовали следующую промежуточную его интерпретацию: .Так как в режиме тяги тормоза поезда не применяются, а ускорение равно нулю получим: 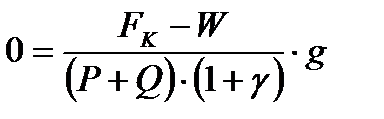.С учетом того, что сила тяги и скорость равны расчетной, получим следующее выражение для определения веса поезда по затяжному подъему: 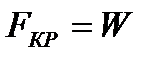;где FКР – расчетная сила тяги локомотивов; W – полное сопротивление движению поезда. С другой стороны, полное сопротивление движению поезда складывается из полного сопротивления движению локомотива (W/) и полного сопротивления движению состава (W//). 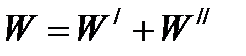.В свою очередь полное сопротивление движению локомотива (W/) состоит из основного сопротивления движению ( 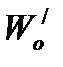) и сопротивления движению от затяжного подъема ( ). Сопротивление движению состава (W//) также состоит из основного сопротивления движению ( 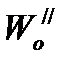) и сопротивления движению от затяжного подъема ( ). 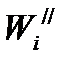.Абсолютные значения сил сопротивления движения локомотива и состава выражаются через их удельные величины: ; ;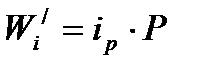 ; ;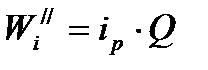где P, Q - вес локомотива и состава соответственно (т); , - основное удельное сопротивление движению локомотива и состава соответственно (кгс/т); ip – величина расчетного (затяжного) подъема о/оо.Более подробно основное и дополнительное сопротивления движению будут рассмотрены отдельно. Подставив полученные слагаемые в одно уравнение получим следующее соотношение: 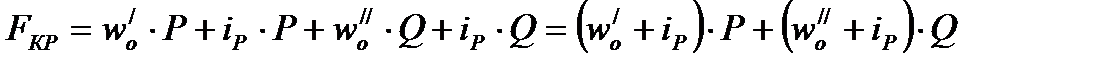.Преобразуя данное выражение относительно веса состава, получим конечную формулу для определения веса состава по затяжному подъему: 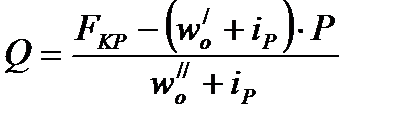.Полученное соотношение позволяет определять допустимый вес состава без учета запаса кинетической энергии поезда. |