Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
«СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ»
(ФГБОУ ВО «СГУГиТ»)
ПРАКТИЧЕСКАЯ РАБОТА №2
Предмет: Мультиагентные системы для управления ресурсами
Тема: Оптимальное размещение распределительного центра
в сети распределения
Преподаватель: канд. тех. наук, доцент Барлиани А.Г.
Выполнил: Квачков А.С., МИ-11
НОВОСИБИРСК 2022
Оптимальное размещение распределительного центра
в сети распределения
Задание 2 На заданной территории представлены населенные пункты (таблица 1). Необходимо оптимально расположить распределительный центр фирмы при следующих условиях:
1) торгующие организации, расположенные в населенных пунктах, будут снабжаться предполагаемым распределительным центром;
2) планируемая годовая норма потребления товарно-материальных ценностей на одного человека – 3 тонны.
Исходные данные
Номера
населенных пунктов
|
Координаты населенных пунктов, км
|
Численность населения,
тыс. чел. Si
|
абсцисса ai
|
ордината bi
|
1
|
131
|
577
|
2,443
|
2
|
302
|
511
|
2,61
|
3
|
561
|
682
|
2,93
|
4
|
162
|
611
|
1,31
|
5
|
286
|
302
|
1,61
|
6
|
411
|
762
|
1,71
|
7
|
531
|
102
|
2,01
|
8
|
621
|
752
|
1,11
|
9
|
862
|
911
|
1,34
|
10
|
552
|
641
|
2,22
|
11
|
61
|
452
|
1,25
|
12
|
912
|
811
|
1,01
|
13
|
622
|
732
|
3,425
|
14
|
157
|
702
|
2,53
|
15
|
902
|
982
|
1,152
|
Пусть точность вычисления составляет 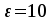 . .
Вычисление приближенных координат предполагаемого распределительного центра
Номера
населенных пунктов
|
Потребность населенного пункта, тыс. т. Qi
|
ai * Qi
|
bi * Qi
|
1
|
7,329
|
320,033
|
1409,611
|
2
|
7,83
|
788,22
|
1333,71
|
3
|
8,79
|
1643,73
|
1998,26
|
4
|
3,93
|
212,22
|
800,41
|
5
|
4,83
|
460,46
|
486,22
|
6
|
5,13
|
702,81
|
1303,02
|
7
|
6,03
|
1067,31
|
205,02
|
8
|
3,33
|
689,31
|
834,72
|
9
|
4,02
|
1155,08
|
1220,74
|
10
|
6,66
|
1225,44
|
1423,02
|
11
|
3,75
|
76,25
|
565
|
12
|
3,03
|
921,12
|
819,11
|
13
|
10,275
|
2130,35
|
2507,1
|
14
|
7,59
|
397,21
|
1776,06
|
15
|
3,456
|
1039,104
|
1131,264
|
Итого
|
85,98
|
12828,65
|
17813,27
|
X0 = 149,2050128; y0 = 207,1791696
Таблица первой итерации
Ri(0)
|
Qi/Ri(0)
|
aiQi/Ri(0)
|
biQi/Ri(0)
|
|
|
370,27
|
0,0198
|
2,59298
|
11,421
|
|
340,08
|
0,023
|
6,95328
|
11,7653
|
|
628,51
|
0,014
|
7,84579
|
9,53802
|
|
404,02
|
0,0097
|
1,5758
|
5,94329
|
|
166,44
|
0,029
|
8,29933
|
8,76363
|
|
613,48
|
0,0084
|
3,43681
|
6,3719
|
|
396,02
|
0,0152
|
8,08532
|
1,55311
|
|
720,71
|
0,0046
|
2,8693
|
3,47458
|
|
1001,7
|
0,004
|
3,45929
|
3,65594
|
|
591,98
|
0,0113
|
6,21017
|
7,21145
|
|
260,23
|
0,0144
|
0,87904
|
6,51358
|
|
972,86
|
0,0031
|
2,84045
|
2,52588
|
|
706,38
|
0,0145
|
9,04762
|
10,6477
|
|
494,88
|
0,0153
|
2,40791
|
10,7666
|
|
1080,3
|
0,0032
|
2,8856
|
3,14153
|
|
Итого
|
0,1896
|
69,3887
|
103,293
|
|
X1 = 365,919; y1 = 544,714
Определим значение целевой функции, которая составляет:
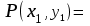 26105т. км. 26105т. км.
Таблица второй итерации
Ri(1)
|
Qi/Ri(1)
|
aiQi/Ri(1)
|
biQi/Ri(1)
|
|
|
237,13
|
0,0309
|
4,048883
|
17,8336
|
|
72,265
|
0,1084
|
32,72203
|
55,3674
|
|
238,55
|
0,0368
|
20,67187
|
25,1305
|
|
214,42
|
0,0183
|
2,969196
|
11,1986
|
|
255,53
|
0,0189
|
5,405876
|
5,7083
|
|
221,91
|
0,0231
|
9,501147
|
17,6153
|
|
472,49
|
0,0128
|
6,776702
|
1,30174
|
|
328,69
|
0,0101
|
6,291523
|
7,61872
|
|
616,65
|
0,0065
|
5,619425
|
5,93886
|
|
209,52
|
0,0318
|
17,54667
|
20,3758
|
|
318,7
|
0,0118
|
0,717754
|
5,31844
|
|
607,55
|
0,005
|
4,548391
|
4,04468
|
|
317,26
|
0,0324
|
20,14455
|
23,7071
|
|
261,51
|
0,029
|
4,556782
|
20,3749
|
|
691,81
|
0,005
|
4,506019
|
4,90567
|
|
Итого
|
0,3808
|
146,0268
|
226,44
|
|
X2 = 383,4596; y2 = 594,6198
Далее необходимо рассчитать целевую функцию:
|
 Скачать 74.04 Kb.
Скачать 74.04 Kb. .
.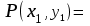 26105т. км.
26105т. км.