Министерство транспорта Российской Федерации
Федеральное агентство железнодорожного транспорта
Федеральное государственно образовательное учреждение высшего образования
«Дальневосточный университет путей сообщения»
Естественно-научный институт
Кафедра «Высшая математика»
Реферат на тему:
«Оптимизация на сетевых моделях»
Выполнил
студентД.С.Петренко
подпись, дата
Проверил
доцент Е.Н. Мурая
подпись, дата
Хабаровск 2022
Оглавление
Введение. 1
Основные методические положения. 2
Основные параметры сетевого графика. 4
Определение продолжительности работ. 7
Оптимизация сетевого графика по времени. 8
Практическая часть 11
Исходные данные: 11
Вывод 14
Библиографический список 14
 Введение. Введение.
До появления сетевых методов планирования работ, проектов осуществлялось в небольшом объеме. Работа была очень затратоемкой и неэффективной.
Современное планирование начинается с разбиения программы работ на операции. Определяются оценки продолжительности операций, и строится сетевая модель (график). Построение сетевой модели позволяет проанализировать все операции и внести улучшения в структуру модели до начала реализации. Строится календарный график, определяющий начало и окончание каждой операции, а также взаимосвязи с другими операциями.
Календарный график выявляет критические операции, которым надо уделять особое внимание, чтобы закончить все операции в директивный срок. Что касается некритических операций, то календарный план позволяет определить резервы времени, которые можно выгодно использовать при задержке выполнения работ или эффективном использовании как трудовых, так и финансовых ресурсов.
Целью данной работы является развитие навыков построения, расчета, анализа и оптимизации сетевого графика.
Основные методические положения.
Для планирования и управления комплексами работ применяются системы сетевого планирования и управления (СПУ). СПУ основано на построении графического изображения определенного комплекса работ, отражающего их логическую последовательность, взаимосвязь и длительность, с последующим анализом и оптимизацией разработанного графика.
Сетевая модель (график, сеть) представляет собой графическую модель, в которой изображаются взаимосвязи и результаты всех работ планируемого комплекса.
Основными элементами графика являются события и работы.
Событие – это результат выполнения одной или нескольких работ. Событие – это свершившийся факт, оно занимает лишь один момент во времени и не имеет продолжительности. Оно указывает на начало каких-либо работ и может быть одновременно итогом завершения других работ. Различают две группы событий: для всей группы работ – исходное I и завершающие J, а для каждой работы – начальное i и конечное j.
В сетевом графике событие изображается геометрической фигурой (кружком, квадратом и т.д.), в котором указывается порядковый номер или шифр события, а иногда и название события.
Работами называются любые процессы, действия, приводящие к достижению определенных результатов (событий).
Работа может быть действительной или фиктивной. Действительная работа – это процесс, требующий затрат времени и исполнителей. Графически действительная работа изображается сплошной линией со стрелкой, которая означает затрату времени, необходимого для выполнения данной работы. Затрачиваемое на работу время обозначается над стрелкой, а число исполнителей под стрелкой. Фиктивная работа устанавливает только логическую связь между работами, она не требует затрат времени и исполнителей, на сетевом графике изображается пунктирной линией.
Любая последовательность в сетевом графике, в которой конечное событие одной работы совпадает с начальным событием следующей за ней работы, называет путем. В сетевом графике следует различать несколько видов путей:
а) от исходного события до завершающего события – полный путь
б) от исходного события до данного – путь, предшествующий данному событию
в) от данного события до завершающего – путь, последующий за данным событием
г) между двумя какими-либо промежуточными событиями i и j – путь между событиями i и j
д) путь между исходным и завершающим событием, имеющий наибольшую продолжительность – критический путь.
Сетевое планирование и управление включает семь этапов:
составление перечня работ, которые надлежит выполнить по объекту разработки для получения конечной цели.
установление топологии сети
построение сетевого графика
определение продолжительности работ
расчет параметров сети
анализ сети и оптимизация сетевого графика
функционирование сетевой модели.
Правила построения сетевого графика:
При построении сетевого графика необходимо соблюдать технологическую последовательность выполняемых работ планируемого комплекса.
В сетевом графике не должно быть пересекающихся стрелок.
Направление стрелок в сетевом графике должно быть слева на право.
В сетевом графике не должно быть событий, которым не предшествует ни одна работа (кроме исходной).
В построенном сетевом графике должно быть одно начальное и одно завершенное событие.
В сетевом графике необходимо соблюдать последовательность в нумерации событий от исходного, которому обычно присваивается нулевой номер, к завершающему. При этом для любой работы i-j одним из условий правильного построения сетевого графика является обязательным выполнение неравенства i Основные параметры сетевого графика.
К основным параметрам сетевого графика относятся критический путь, резервы времени событий и работ. Эти параметры являются исходными для получения ряда дополнительных характеристик, а так же для анализа сети.
Критическим путем называют наибольший по продолжительности из всех путей сетевого графика от исходного события до завершающего. В сетевом графике имеются и другие пути, опирающиеся на исходное и завершающее события (полные пути), которые могут либо полностью проходить вне критического пути, либо частично совпадать с критической последовательностью работ. Эти пути называются не напряженными. Ненапряженные пути – это полные пути сетевого графика, которые по продолжительности меньше критического пути.
Ненапряженные пути обладают важным свойством: на участках, не совпадающих с критической последовательностью работ, они имеют резервы времени. Это означает, что задержка в совершении событий, не лежащих на критическом пути, до определенного момента не влияет на срок завершения разработки в целом. Критические пути резервами времени не располагают.
Резервы времени события – это такой промежуток времени, на который может быть отсрочено совершение этого события без нарушения сроков завершения разработки в целом.
Резерв времени события Ri определяет как разность между поздним Тпi и ранним Трi сроками наступления события:
Ri = Тпi - Трi (1)
Поздний срок Тпi – это такой срок завершения i-го события, превышение которого вызовет задержку завершения события.
Ранний из возможных сроков совершения i-го события Трi – минимальный срок, необходимый для выполнения всех работ, предшествующих данному событию.
Ранний срок совершения события i определяется как продолжительность во времени максимального из путей Lmax, ведущих от исходного события I до данного события i:
Трi = t [ L (I – i)max ] (2)
Поздний срок события I определяется по следующей формуле:
Тпi = t (Lкр) – t [ L ( i – C)max ] (3)
Путь, соединяющий события с нулевыми резервами времени, является критическим.
Резервами времени так же располагают работы. Зная ранние и поздние сроки наступления событий, можно для любой работы (i,j) определить ранние и поздние сроки начала и окончания работ.
Ранний срок начала работ:
Tрн i,j = Трi (4)
Поздний срок начала этой работы:
Tпн i,j = Тпσ – t i,j (5)
Ранний срок окончания работ:
Tро i,j = Трi + t i,j (6)
Поздний срок окончания работ:
Tпо i,j = Тпj (7)
Разница во времени между длиной критического пути t ( Lкр ) и длиной любого другого пути t ( Li ) называется полным резервом времени пути. Он равен:
R (Li) = t ( Lкр ) – t ( Li ) (8)
Полный резерв пути показывает, насколько могут быть увеличены продолжительности всех работ, принадлежавших пути Li.
Полный резерв времени работы Rп i,j показывает, сколько имеется в запасе времени для выполнения данной работы, на которое можно увеличить продолжительность данной работы, не изменяя при этом продолжительности данного пути:
Rп i,j = Тпj - Трi - t i,j (9)
У отдельных видов работ помимо полного резерва времени имеется свободный резерв времени Rс i,j, являющийся частью резерва. На время этого резерва можно увеличить продолжительность работы, не изменяя ранних сроков начала последующих работ.
Rс i,j = Трj - Трi - t i,j (10)
Резервы времени работ, особенно свободный, позволяют маневрировать сроками начала и окончания работ, их продолжительностью.
Определение продолжительности работ.
При построенной сетевой модели для каждой работы определяется ожидаемая продолжительность ее выполнения, которая проставляется над соответствующей стрелкой в графике. Для определения продолжительности работ пользуются установленными нормами времени, при их отсутствии используют систему вероятностных оценок. В таких случаях ожидаемое время выполнения работ ti,j определяют на основе экспертных оценок по формуле
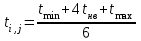 (11) (11)
Дисперсия, или мера разброса для принятого в СПУ закона распределения:
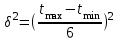 (12) (12)
Для двух оценок:
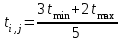 (13) (13)
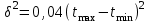 (14) (14)
где tmin – минимально возможное время выполнения работ;
tmax – максимально возможное время выполнения работ;
tнв – наиболее вероятное время выполнения работ.
Расчет параметров сетевого графика графическим методом.
Существует несколько методов расчета сетевых графиков: графический, табличный, матричный, метод Форда и др.
Графический метод можно применять в тех случаях, когда число событий невелико (до 15-20). При этом каждый кружок, изображающий событие, делится на четыре сектора (рис.1).
  
Rci,j
ti,j
Rni,j
 
   
Bi,j

Рис. 1. Секторы событий сетевого графика
Верхний сектор отводится для номера события; левый – для ранних сроков свершения событий; правый – для поздних сроков свершения событий; нижний – для резервов времени свершения событий; левая часть стрелки – для полного резерва работы; правая часть стрелки – для свободного резерва работы.
Расчет параметров сетевого графика табличным методом.
Для больших сетевых моделей целесообразно использовать табличный метод расчета, который позволяет определить параметры сети непосредственно в таблице по определенным правилам.
Построение карты проекта сетевого графика.
После расчета параметров сетевой график вычерчивается в масштабе времени, т. е. строится карта проекта выполнения работ; вначале вычерчивается работы критического пути, а затем остальные работы. В том же масштабе времени строятся графики загрузки исполнителей с учетом их специализации с учетом их специализации и квалификации.
Оптимизация сетевого графика по времени.
Цель оптимизации по времени – сократить продолжительность критического пути, выравнить продолжительность полных путей.
Оптимизация по времени необходима в том случае, если установленный директивный срок выполнения комплекса работ меньше срока свершения завершающего события (Тд < Ткр) и вероятность свершения завершающего события выходит за пределы 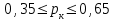 . При рк< 0,35 велика опасность нарушения заданного срока свершения завершающего события. При рк > 0,65 – на работах критического пути имеются избыточные ресурсы. Вероятность свершения завершающего события в директивный срок является функцией случайной величины х: рк = f (x), где . При рк< 0,35 велика опасность нарушения заданного срока свершения завершающего события. При рк > 0,65 – на работах критического пути имеются избыточные ресурсы. Вероятность свершения завершающего события в директивный срок является функцией случайной величины х: рк = f (x), где
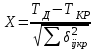 (15) (15)
Функция рк+ определяется по таблице значений нормальной функции распределения вероятностей.
Сокращения продолжительности критического пути можно достичь:
а) Путем изменения топологии сети. При этом следует проверить целесообразность установленного уровня детализации работ и в случае необходимости расчленить некоторые работы иным образом, чем в первоначальном варианте.
Цель при этом – увеличение числа параллельно выполняемых работ, например, работу по изготовлению технологической оснастки можно разделить на работы по изготовлению пресс-форм, штампов, приспособлений для механической обработки, приспособлений для сборочных работ. Все четыре работы выполняются параллельно.
б) Путем интенсификации выполнения работ критического пути.
в) Путем перераспределения ресурсов между работами сетевого графика. Часть ресурсов (рабочая сила, оборудование, финансовые средства) снимается с работ, имеющих большие резервы времени, и распределяется на работе критического пути. В результате такого перераспределения продолжительность ненапряженных работ увеличится, а работ критического пути уменьшится.
Перед проведением оптимизации необходимо определить степень напряженности выполнения каждой работы (кроме работ критического пути), которая характеризуется коэффициентом напряженности работ:
 (16) (16)
Работа с коэффициентом напряженности Кнi,j = 0,8-0,9 относятся к критической зоне и называются работами подкритического пути. Работы с Кн<0.8 имеют часть свободных ресурсов, которые могут быть сняты и переданы для использования их на работах критического и подкритического пути. У работ критического пути Кн = 1. Работы, располагающие одинаковыми полными резервами Rni,j, могут иметь разные Кнi,j.
Объем работ, с которых предполагается перевести исполнителей на работы критического пути, определяется по формуле
Qi,j = ti,j * Bi,j. (17)
Численность исполнителей, которые могут быть переведены с работы (i,j) на работы критического пути, определяется по формулам:
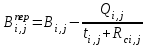 (18) (18)
или
 (19) (19)
Определяется численность исполнителей после оптимизации для работ (i,j)
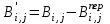 (20) (20)
Определяется численность исполнителей после оптимизации на работах критического пути:
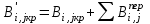 (21) (21)
Определяется продолжительность работ после оптимизации:
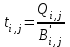 (22) (22)
Оптимизация сетевого графика по ресурсам.
Цель оптимизации сетевого графика по ресурсам – выравнять загрузку исполнителей и сократить численность занятых.
Оптимизация по ресурсам проводится путем изменения срока начала и окончания работ напряженных путей в пределах полного резерва Rn i,j.
Оптимизация проводится в следующей последовательности:
Составляется карта проекта
По диаграмме ежедневной потребности и по календарному графику последовательно рассматриваются участки графика и анализируется возможность сдвига вправо работ участка, при этом применяется следующая очередность оставления работ на участке:
Работы критического пути;
Работы, не законченные в предыдущем периоде;
Работы в последовательности уменьшения полного резерва, при этом учитывается фронт и коэффициенты напряженности работ.
Последовательно рассматривая каждый участок, можно достичь соблюдения заданных условий (сроков, числа, исполнителей).
Практическая часть Исходные данные:
i, j
|
0,1
|
1,2
|
1,3
|
2,4
|
2,6
|
3,4
|
3,5
|
4,5
|
5,7
|
5,8
|
6,9
|
6,10
|
7,8
|
8,9
|
9,10
|
t min
|
5
|
8
|
4
|
1
|
1
|
1
|
14
|
1
|
3
|
2
|
2
|
4
|
1
|
8
|
4
|
t max
|
10
|
13
|
9
|
6
|
3,5
|
3,5
|
19
|
6
|
8
|
7
|
4,5
|
9
|
6
|
13
|
9
|
Bi,j
|
10
|
4
|
3
|
2
|
5
|
4
|
2
|
3
|
4
|
3
|
5
|
5
|
3
|
5
|
3
|
Определение продолжительности работ Таблица 1
Код работы
|
t min
|
t max
|
B i,j
|
t i,j
|
σ 2
|
0,1
|
5
|
10
|
10
|
7
|
1
|
1,2
|
8
|
13
|
4
|
10
|
1
|
1,3
|
4
|
9
|
3
|
6
|
1
|
2,4
|
1
|
6
|
2
|
3
|
1
|
2,6
|
1
|
3,5
|
5
|
2
|
0,25
|
3,4
|
1
|
3,5
|
4
|
2
|
0,25
|
3,5
|
14
|
19
|
2
|
16
|
1
|
4,5
|
1
|
6
|
3
|
3
|
1
|
5,7
|
3
|
8
|
4
|
5
|
1
|
5,8
|
2
|
7
|
3
|
4
|
1
|
6.9
|
2
|
4,5
|
5
|
3
|
0,25
|
6,10
|
4
|
9
|
5
|
6
|
1
|
7,8
|
1
|
6
|
3
|
3
|
1
|
8,9
|
6
|
13
|
5
|
10
|
1
|
9,10
|
4
|
9
|
3
|
6
|
1
|
Расчет ожидаемой продолжительности работ (t i,j) и дисперсии (σ 2):
t0,1 = (3*5+2*10)/5 = 7 σ 2 = 0,04 (10 – 5) 2 = 1
t1,2 = (3*8+2*13)/5 = 10 σ 2 = 0,04 (13 – 8) 2 = 1
t1,3 = (3*4+2*9)/5 = 6 σ 2 = 0,04 (9 – 4) 2 = 1
t2,4 = (3*1+2*6)/5 = 3 σ 2 = 0,04 (6 – 1) 2 = 1
t2,6 = (3*1+2*3,5)/5 = 2 σ 2 = 0,04 (3,5 – 1) 2 = 0,25
t3,4 = (3*1+2*3,5)/5 = 2 σ 2 = 0,04 (3,5 – 1) 2 = 0,25
t3,5 = (3*14+2*19)/5 = 16 σ 2 = 0,04 (19 – 14) 2 = 1
t4,5 = (3*1+2*6)/5 = 3 σ 2 = 0,04 (6 – 1) 2 = 1
t5,7 = (3*3+2*8)/5 = 5 σ 2 = 0,04 (8 – 3) 2 = 1
t5,8 = (3*2+2*7)/5 = 4 σ 2 = 0,04 (7 – 2) 2 = 1
t6,9 = (3*2+2*4,5)/5 = 3 σ 2 = 0,04 (4,5 – 2) 2 = 0,25
t6,10 = (3*4+2*9)/5 = 6 σ 2 = 0,04 (9 – 4) 2 = 1
t7,8 = (3*1+2*6)/5 = 3 σ 2 = 0,04 (6 – 1) 2 = 1
t8,9 = (3*8+2*13)/5 = 10 σ 2 = 0,04 (13 – 8) 2 = 1
t9,10 = (3*4+2*9)/5 = 6 σ 2 = 0,04 (9 – 4) 2 = 1
Расчет параметров сетевого графика графическим методом
Результаты данных расчетов занесены в таблицу 2:
i,j
|
t i,j
|
T pj
|
Tnj
|
Rj
|
Tpi
|
TpHi,j
|
Tpoi,j
|
TnHi,j
|
Tnoi,j
|
Rni,j
|
Rci,j
|
0,1
|
7
|
7
|
7
|
0
|
0
|
0
|
7
|
0
|
7
|
0
|
0
|
1,2
|
10
|
17
|
23
|
6
|
7
|
7
|
17
|
13
|
23
|
6
|
0
|
1,3
|
6
|
13
|
13
|
0
|
7
|
7
|
13
|
7
|
13
|
0
|
0
|
2,4
|
3
|
20
|
26
|
6
|
17
|
17
|
20
|
23
|
26
|
6
|
0
|
2,6
|
2
|
19
|
44
|
25
|
17
|
17
|
19
|
42
|
44
|
25
|
0
|
3,4
|
2
|
20
|
26
|
6
|
13
|
13
|
15
|
24
|
26
|
11
|
5
|
3,5
|
16
|
29
|
29
|
0
|
13
|
13
|
29
|
13
|
29
|
0
|
0
|
4,5
|
3
|
29
|
29
|
0
|
20
|
20
|
23
|
26
|
29
|
6
|
6
|
5,7
|
5
|
34
|
34
|
0
|
29
|
29
|
34
|
29
|
34
|
0
|
0
|
5,8
|
4
|
37
|
37
|
0
|
29
|
29
|
33
|
33
|
37
|
4
|
4
|
6.9
|
3
|
47
|
47
|
0
|
19
|
19
|
22
|
44
|
47
|
25
|
25
|
6,10
|
6
|
53
|
53
|
0
|
19
|
19
|
25
|
47
|
53
|
28
|
28
|
7,8
|
3
|
37
|
37
|
0
|
34
|
34
|
37
|
34
|
37
|
0
|
0
|
8,9
|
10
|
47
|
47
|
0
|
37
|
37
|
47
|
37
|
47
|
0
|
0
|
9,10
|
6
|
53
|
53
|
0
|
47
|
47
|
53
|
47
|
53
|
0
|
0
|
Подробности расчетов некоторых из показателей:
TpH i,j = Tpi
Tpo 0,1 = 0+7 = 7; Tpo 1,2 = 7+10 = 17; Tpo 1,3 = 7+6 = 13;
Tpo 2,4 = 17+3 = 20; Tpo 2,6 = 17+2 = 19; Tpo 3,4 = 13+2 = 15;
Tpo 3,5 = 13+16 = 29; Tpo 4,5 = 20+3 =23; Tpo 5,7 = 29+5 = 34;
Tpo 5,8 = 29+4 = 33; Tpo 6,9 = 19+3 = 22; Tpo 6,10 = 19+6 = 25;
Tpo 7,8 = 34+3 = 37; Tpo 8,9 = 37+10 = 47; Tpo 9,10 = 47+6 = 53.
TnH 0,1 = 7 – 7 = 0; TnH 1,2 = 23 – 10 = 13; TnH 1,3 = 13 – 6 = 7;
TnH 2,4 = 26 – 3 = 23; TnH 2,6 = 44 – 2 = 42; TnH 3,4 = 26 – 2 = 24;
TnH 3,5 = 29 – 16 = 13; TnH 4,5 = 29 – 3 = 26; TnH 5,7 = 34 – 5 = 29;
TnH 5,8 = 37 – 4 = 33; TnH 6,9 = 47 – 3 = 44; TnH 6,10 = 53 – 6 = 47;
TnH 7,8 = 37 – 3 = 34; TnH 8,9 = 47 – 10 = 37; TnH 9,10 = 53 – 6 = 47.
Tnoi,j = Tnj
Rn0,1 = 7–0–7 = 0; Rn1,2 = 23–7–10 = 6; Rn1,3 = 13–7–6 = 0;
Rn2,4 = 26–17–3 = 6; Rn2,6 = 44–17–2 = 25; Rn3,4 = 26–13–2 = 11;
Rn3,5 = 29–13–16 = 0; Rn4,5 = 29–20–3 = 6; Rn5,7 = 34–29–5 = 0;
Rn5,8 = 37–29–4 = 4; Rn6,9 = 47–19–3 = 25; Rn6,10 = 53–19–6 = 28;
Rn7,8 = 37–34–3 = 0; Rn8,9 = 47–37–10 = 0; Rn9,10 = 53–47–6 = 0;
Rc 0,1 = 7–0–7 = 0; Rc 1,2 = 17–7–10 = 0; Rc 1,3 = 13–7–6 = 0;
Rc 2,4 = 20–17–3 = 0; Rc 2,6 = 19–17–2 = 0; Rc 3,4 = 20–13–2 = 5;
Rc 3,5 = 29–13–16 = 0; Rc 4,5 = 29–20–3 = 6; Rc 5,7 = 34–29–5 = 0;
Rc 5,8 = 37–29–4 = 4; Rc 6,9 = 47–19–3 = 25; Rc 6,10 = 53–19–6 = 28;
Rc 7,8 = 37–34–3 = 0; Rc 8,9 = 47–37–10 = 0; Rc 9,10 = 53–47–6 = 0;
Определяем продолжительность критического пути (Rj = 0)
t (Lkp) = 7+6+16+3+5+4+3+6+3+10+6 = 66
Расчет параметров сетевого графика табличным методом.
Таблица 3
Код
работ
|
Кол-во предшед. работ
|
t i,j
|
TpHi,j
|
Tpoi,j
|
TnHi,j
|
Tnoi,j
|
Rni,j
|
Rci,j
|
Rj
|
Коды работ Lkp
|
0,1
|
0
|
7
|
0
|
7
|
0
|
7
|
0
|
0
|
0
|
0,1
|
1,2
|
1
|
10
|
7
|
17
|
13
|
23
|
6
|
0
|
6
|
|
1,3
|
1
|
6
|
7
|
13
|
7
|
13
|
0
|
0
|
0
|
1,3
|
2,4
|
1
|
3
|
17
|
20
|
23
|
26
|
6
|
0
|
6
|
|
2,6
|
1
|
2
|
17
|
19
|
42
|
44
|
25
|
0
|
25
|
|
3,4
|
1
|
2
|
13
|
15
|
24
|
26
|
11
|
5
|
6
|
|
3,5
|
1
|
16
|
13
|
29
|
13
|
29
|
0
|
0
|
0
|
3,5
|
4,5
|
2
|
3
|
20
|
23
|
26
|
29
|
6
|
6
|
0
|
|
5,7
|
2
|
5
|
29
|
34
|
29
|
34
|
0
|
0
|
0
|
5,7
|
5,8
|
2
|
4
|
29
|
33
|
33
|
37
|
4
|
4
|
0
|
|
6.9
|
1
|
3
|
19
|
22
|
44
|
47
|
25
|
25
|
0
|
|
6,10
|
1
|
6
|
19
|
25
|
47
|
53
|
28
|
28
|
0
|
|
7,8
|
1
|
3
|
34
|
37
|
34
|
37
|
0
|
0
|
0
|
7,8
|
8,9
|
2
|
10
|
37
|
47
|
37
|
47
|
0
|
0
|
0
|
8,9
|
9,10
|
2
|
6
|
47
|
53
|
47
|
53
|
0
|
0
|
0
|
9,10
|
Подробности расчетов некоторых показателей:
TpH 0,1 = 0; TpH 1,2 = 0+7 = 7; TpH 1,3 = 0+7 = 7;
TpH 2,4 = 7+10 = 17; TpH 2,6 = 7+10 = 17; TpH 3,4 = 7+6 = 13;
TpH 3,5 = 7+6 = 13; TpH 4,5 = 17+3 = 20; TpH 5,7 = 13+16 = 29;
TpH 5,8 = 13+16 = 29; TpH 6,9 = 17+2 = 19; TpH 6,10 = 17+2 = 19;
TpH 7,8 = 29+5 = 34; TpH 8,9 = 34+3 = 37; TpH 9,10 = 37+10 = 47.
Tpo 0,1 = 0+7 = 7; Tpo 1,2 = 7+10 = 17; Tpo 1,3 = 7+6 = 13;
Tpo 2,4 = 17+3 = 20; Tpo 2,6 = 17+2 = 19; Tpo 3,4 = 13+2 = 15;
Tpo 3,5 = 13+16 = 29; Tpo 4,5 = 20+3 = 23; Tpo 5,7 = 29+5 = 34;
Tpo 5,8 = 29+4 = 33; Tpo 6,9 = 19+3 = 22; Tpo 6,10 = 19+6 = 25;
Tpo 7,8 = 34+3 = 37; Tpo 8,9 = 37+10 = 47; Tpo 9,10 = 47+6 = 53;
Tno 9,10 = 53; Tno 8,9 = 53–6 = 47; Tno 7,8 = 47–10 = 37;
Tno 6,10 = 53; Tno 6,9 = 53–6 = 47; Tno 5,8 = 47–10 = 37;
Tno 5,7 = 37–3 = 34; Tno 4,5 = 33–4 = 29; Tno 3,5 = 33–4 = 29;
Tno 3,4 = 29–3 = 26; Tno 2,6 = 47–3 = 44; Tno 2,4 = 29–3 = 26;
Tno 1,3 = 29–16 = 13; Tno 1,2 = 26–3 = 23; Tno 0,1 = 13–6 = 7;
TnH 0,1 = 7–7 = 0; TnH 1,2 = 23–10 = 13; TnH 1,3 = 13–6 = 7;
TnH 2,4 = 26–3 = 23; TnH 2,6 = 44–2 = 42; TnH 3,4 = 26–2 = 24;
TnH 3,5 = 29–16 = 13; TnH 4,5 = 29–3 = 26; TnH 5,7 = 34–5 = 29;
TnH 5,8 = 37–4 = 33; TnH 6,9 = 47–3 = 44; TnH 6,10 = 53–6 = 47;
TnH 7,8 = 37–3 = 34; TnH 8,9 = 47–10 = 37; TnH 9,10 = 53–6 = 47;
Rn 0,1 = 7–7 = 0; Rn 1,2 = 23–17 = 6; Rn 1,3 = 13–13 = 0;
Rn 2,4 = 26–20 = 6; Rn 2,6 = 44–19 = 25; Rn 3,4 = 26–15 = 11;
Rn 3,5 = 29–29 = 0; Rn 4,5 = 29–23 = 6; Rn 5,7 = 34–34 = 0;
Rn 5,8 = 37–33 = 4; Rn 6,9 = 47–22 = 25; Rn 6,10 = 53–25 = 28;
Rn 7,8 = 37–37 = 0; Rn 8,9 = 47–47 = 0; Rn 9,10 = 53–53 = 0;
R1 = 7–7 = 0; R2 = 23–17 = 6; R3 = 13–13 = 0;
R4 = 26–20 = 6; R5 = 44–19 = 25; R6 = 26–20 = 6;
R7 = 29–29 = 0; R8 = 29–29 = 0; R9 = 34–34 = 0;
R10 = 37–37 = 0; R11 = 47–47 = 0; R12 = 53–53 = 0
R13 = 37–37 = 0; R14 = 47–47 = 0; R15 = 53–53 = 0;
Rc 0,1 = 0–0 = 0; Rc 1,2 = 6–6 = 0; Rc 1,3 = 0–0 = 0;
Rc 2,4 = 6–6 = 0; Rc 2,6 = 25–25 = 0; Rc 3,4 = 11–6 = 5;
Rc 3,5 = 0–0 = 0; Rc 4,5 = 6–0 = 6; Rc 5,7 = 0–0 = 0;
Rc 5,8 = 4–0 = 4; Rc 6.9 = 25–0 = 25; Rc 6,10 = 28–0 = 28;
Rc 7,8 = 0–0 = 0; Rc 8,9 = 0–0 = 0; Rc 9,10 = 0–0 = 0;
Вывод
В ходе данной работы были развиты навыки построения, расчета, анализа и оптимизации сетевого графика. Так же были выполнены расчеты ожидаемой продолжительности выполнения работ графическим и табличным методами, построены топологическая модель и карта проекта сетевого графика. В ходе работы производились расчеты показателей Х и Кн и дальнейшая оптимизация сетевого графика по времени в результате чего, был сокращен заданный критический путь на 10 дней, с дальнейшей перестройкой оптимизированной карты проекта и перерасчетом важнейших показателей. В ходе оптимизации сетевого графика были совершены действия направленные на более рациональное использование трудовых ресурсов с их равномерным размещением по каждому рабочему дню, таким образом количество задействованных работников на каждый день не превышало десяти исполнителей.
Библиографический список |
 Скачать 92.64 Kb.
Скачать 92.64 Kb.
 Введение.
Введение.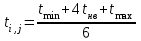 (11)
(11)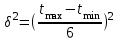 (12)
(12)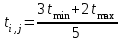 (13)
(13)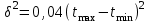 (14)
(14)







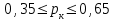 . При рк< 0,35 велика опасность нарушения заданного срока свершения завершающего события. При рк > 0,65 – на работах критического пути имеются избыточные ресурсы. Вероятность свершения завершающего события в директивный срок является функцией случайной величины х: рк = f (x), где
. При рк< 0,35 велика опасность нарушения заданного срока свершения завершающего события. При рк > 0,65 – на работах критического пути имеются избыточные ресурсы. Вероятность свершения завершающего события в директивный срок является функцией случайной величины х: рк = f (x), где
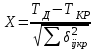 (15)
(15) (16)
(16)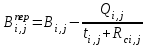 (18)
(18) (19)
(19)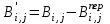 (20)
(20)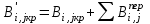 (21)
(21)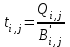 (22)
(22)