Оптимизация плана перевозок продукта от поставщиков к потребителям по критерию минимизации транспортных издержек. 2 лаб. Оптимизация плана перевозок продукта от поставщиков к потребителям по критерию минимизации транспортных издержек по дисциплине Системный анализ и принятие решений
 Скачать 339.2 Kb. Скачать 339.2 Kb.
|
|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА» (СПбГУТ) Кафедра автоматизация предприятий связи ОТЧЁТ по лабораторной работе №2 на тему: «Оптимизация плана перевозок продукта от поставщиков к потребителям по критерию минимизации транспортных издержек» по дисциплине «Системный анализ и принятие решений» Вариант №8 Выполнила: студентка группы ИСТ-711 Чуприна К.С. Проверил: ассистент Банцер Е.А. Санкт-Петербург 2020 Цель выполнения работы Цель выполнения лабораторной работы – расчет оптимального плана перевозок продукции от поставщиков к потребителям, который бы минимизировал суммарные затраты на перевозку товара. Постановка транспортной задачи Пусть имеются пункты производства А1,…,Аn с объемами производства соответственно а1,…,an и пункты потребления В1,…,Вm с объемами потребления b1,…,bm соответственно. Предполагается, что из каждого пункта производства возможна транспортировка в любой пункт потребления. Известны затраты cij (транспортные издержки) на перевозку единицы продукции из пункта производства i в пункт потребления j. Требуется найти такой план перевозки продукта, при котором: - весь продукт из пунктов производства будет вывезен полностью (без остатков); - запросы потребителей будут полностью удовлетворены; - суммарные затраты на перевозку продукта будут минимальны. Описание системы Система уровня «Логистическое предприятие». Элементы системы: элемент типа «Поставщик», элемент типа «Потребитель». Параметр, которым характеризуется элемент типа «Поставщик»: количество производимой продукции. Параметр, которым характеризуется элемент типа «Потребитель»: потребность потребителя. Параметр, характеризующий связь элементов «Поставщик-Потребитель»: затраты на перевозку единицы продукции. Цель системы – минимизировать суммарные транспортные затраты на перевозку продукции при выполнении заданных условий. Управляемые переменные – количество продукции, перевозимой от поставщика к потребителю. Ограничения системы: полный вывоз продукции от всех поставщиков, полное удовлетворение спроса всех потребителей. Математическая модель транспортной задачи В базовой (закрытой) модели задачи предполагается, что производство продукции и потребление продукта сбалансированы, т.е. 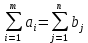 – условие баланса, – условие баланса,где 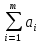 – сумма объемов производства; – сумма объемов производства;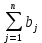 – сумма объемов потребления; – сумма объемов потребления;i – индекс пункта производства; j – индекс пункта потребления. Управляемые переменные. xij – количество продукта, перевозимое из пункта производства i в пункт потребления j; Целевая функция. F – суммарные затраты на перевозку продукта. Тогда минимизация затрат на транспортировку продукции имеет вид: 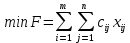 , , где cij – транспортные издержки; min F – минимально возможное значение суммарных транспортных издержек. Система ограничений: Условия полного вывоза продукции 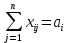 , где i = [1, n]; , где i = [1, n];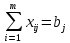 , где j = [1, m]; , где j = [1, m];Условия неотрицательности переменных 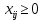 . .Данная модель представляет собой каноническую задачу линейного программирования с (m x n) переменными и (m + n) ограничениями типа равенств. Замечания: Если все параметры принимают целочисленные значения, то и переменные xij в оптимальном решении принимают целочисленные значения; При запрете на некоторые перевозки соответствующие значения xij принимаются равными 0, либо cij = ∞. Функциональные возможности программы Lindo Lindo – пакет прикладных программ, обеспечивающих решение задач линейного программирования (ЛП) и частично-целочисленного программирования (ЧЦП). Рабочая версия программы позволяет решать задачи, содержащие до 100 тыс. и до 32 тыс. ограничений. Система является командно-ориентированной, т.е. для работы с ней используется широкий диапазон команд в зависимости от контекста выполняемой задачи. Также имеется возможность, как ручного ввода информации, так и загрузки данных из файла. Для решения ЗЛП используется симплекс-метод с мультипликативным представлением обратной матрицы, а для решения задач ЧЦП – метод «ветвей и границ» (метод Лэнда и Дойга). На каждом шагу ветвления в процессе решения задачи ЧЦП используется модифицированный симплекс-метод. Результаты расчетов выводятся на экран, а также могут быть выведены на принтер или в отдельный файл. При работе с системой используются 2 диалоговых окна. В первое вводятся данные о переменных, целевой функции и ограничениях. Во втором окне отражаются результаты вычислений: значение целевой функции и переменных, количество итераций и т.д. ЗЛП и задачи ЧЦП могут вводиться в произвольном виде (т.е. в том виде, в котором они формулируются), без необходимости приведения их к какой-либо стандартной форме. Задачи могут решаться, как при поиске минимума целевой функции, так и при поиске максимума. Ограничения могут являться и равенствами, и неравенствами (>, ≥, <, ≤). Описание деловой ситуации Составить оптимальный план прикрепления потребителей продукции к ее поставщикам, обеспечивающий минимальные затраты на перевозку продукции при следующих входных данных: Возможности поставщиков (в тоннах) (см. таблицу 1) Таблица 1 - Возможности поставщиков
Потребности потребителей (в тоннах) (см. таблицу 2) Таблица 2 - Спрос
Затраты на перевозку продукции от i-го поставщика к j-му потребителю (в тыс. руб. на ед. продукции) (см. таблицу 3) Таблица 3 – Затраты на перевозку единицы продукции
Сравнить результат решения поставленной задачи с результатами её решения при условии, что пропускная способность маршрута 1-1 не более 100 т, маршрута 2-4 не более 300 т, маршрута 4-2 не более 220 т. Построение математической модели Тип транспортной задачи Данная задача является транспортной задачей закрытого типа, т.к. 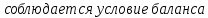 . .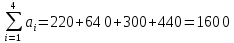 , ,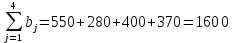 , ,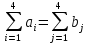 . .Определение управляемых переменных: xij – количество продукции (в тоннах), перевозимое от i-го поставщика к j-му потребителю. Построение целевой функции. Целевая функция – минимум суммарных затрат на перевозку продукции. 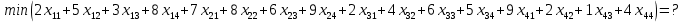 Введение системы ограничений Ограничения, обеспечивающие выполнение условий полного вывоза продукции: 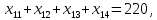 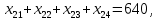 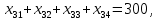 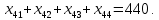 Ограничения, обеспечивающие выполнение условий полного удовлетворения спроса: 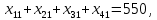 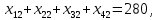 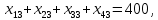 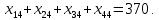 Условие неотрицательности переменных 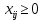 , ,где i ϵ [1, 4] и j ϵ [1, 4]. Анализ результатов решения задачи Для начала, введем задачу в программе Lindo в соответствии с требованиями программы. На рисунке 1 можно видеть постановку задачи для программы Lindo. 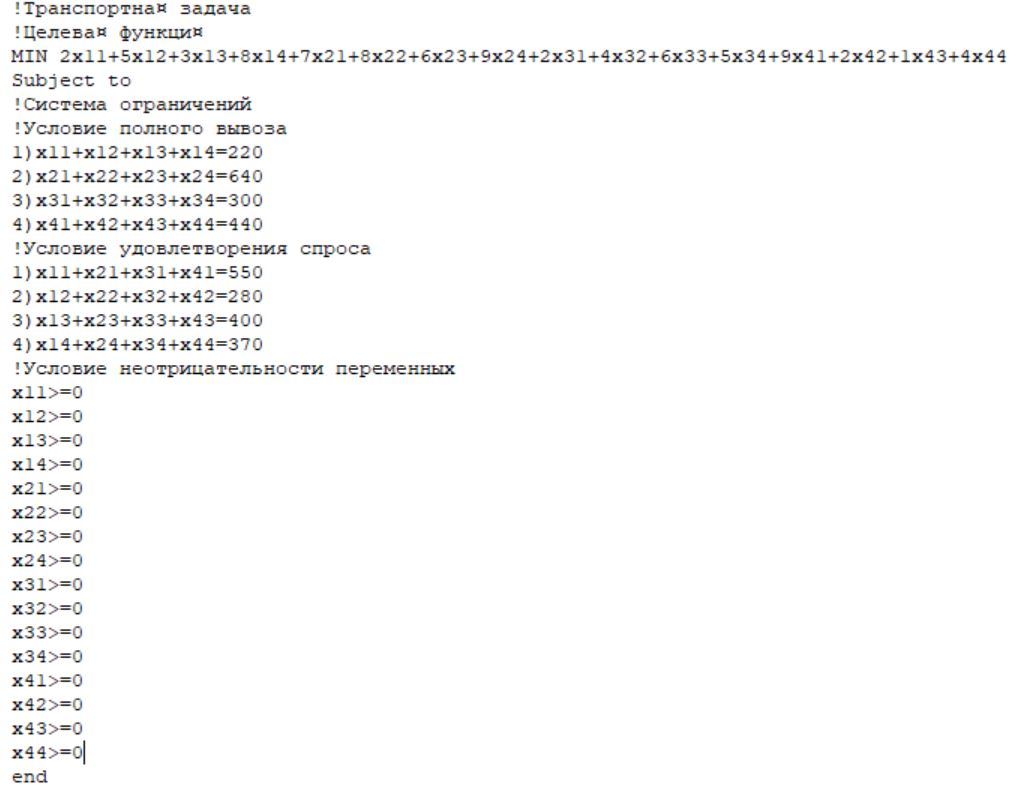 Рисунок 1 – Описание задачи в синтаксисе программы Lindo Решение задачи, полученное с помощью программы Lindo показано на рисунке 2. Также, можно видеть, что данное решение было получено за 9 итераций. 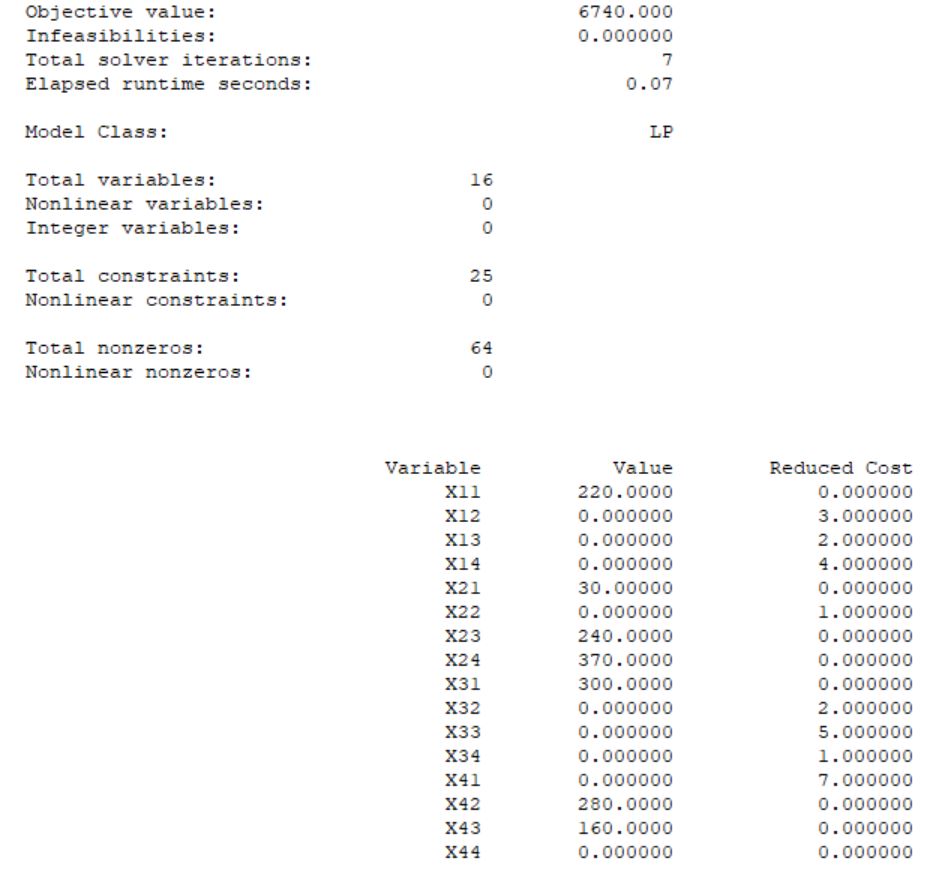 Рисунок 2 – Результат решения транспортной задачи Далее, введем дополнительные условия (ограничения) в описание задачи. Тогда постановка задачи для программы Lindo будет выглядеть в соответствии с рисунком 3. 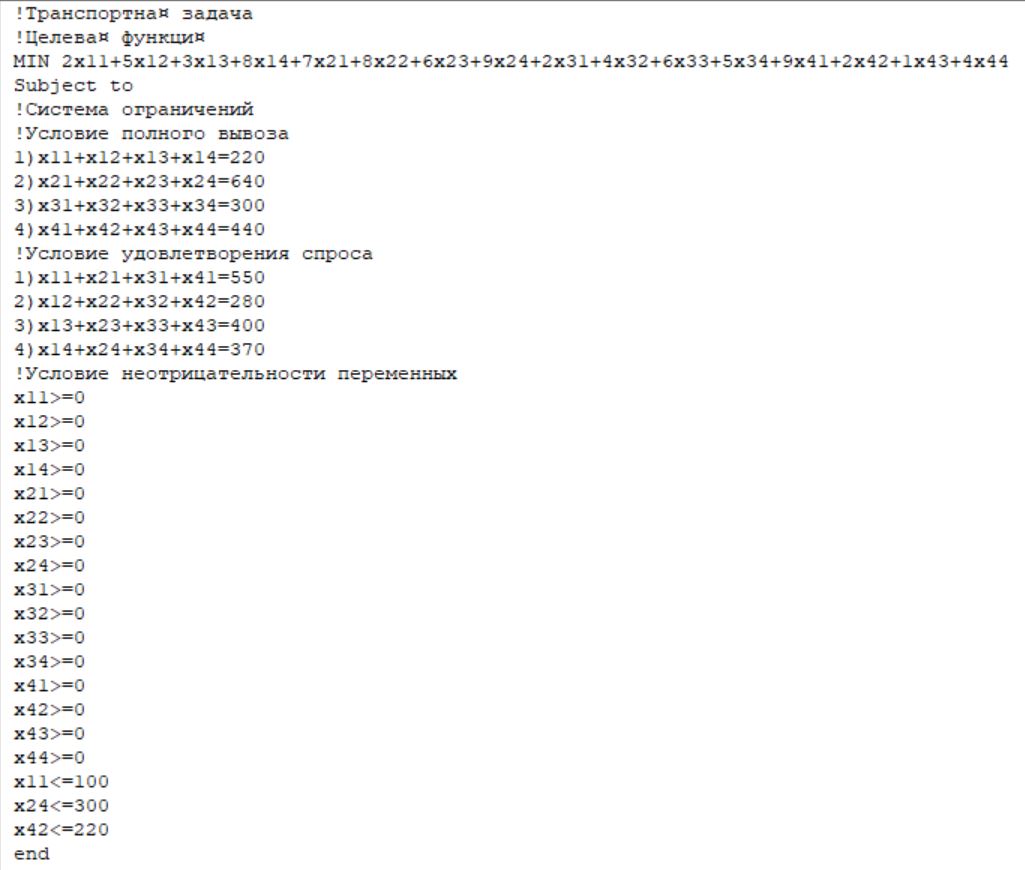 Рисунок 3 - Описание задачи с ограничениями в синтаксисе программы Lindo Результат решения транспортной задачи с ограничениями показан на рисунке 4. 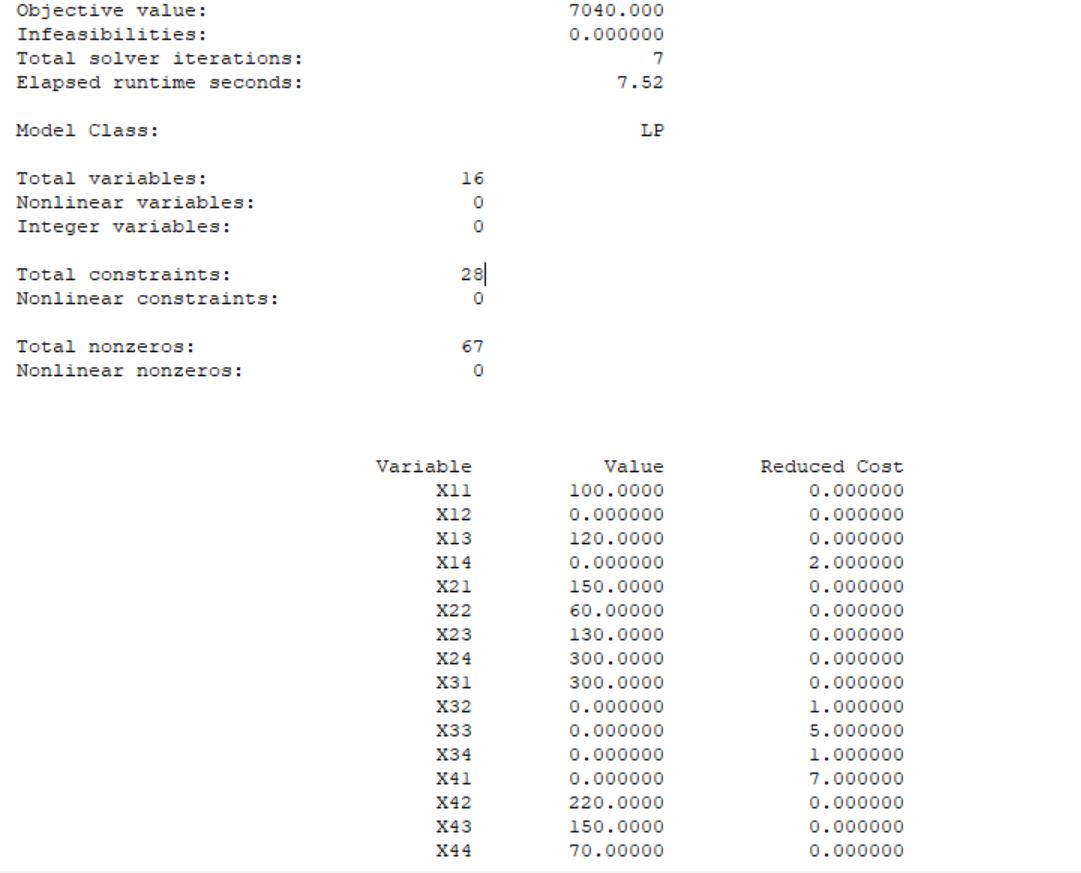 Рисунок 4 – Результат решение транспортной задачи с ограничениями Заключение В ходе данной лабораторной работы была решена транспортная задача закрытого типа – был рассчитан оптимальный план перевозок продукции от поставщиков к потребителям, который бы минимизировал затраты на перевозку продукции. Для решения этой задачи использовался программный продукт Lindo. В результате был получен план перевозок продукции, который является оптимальным. В случае использования этого плана перевозок суммарные затраты составили бы 6740 тыс. руб. Также была решена данная задача с ограничениями на перевозку продукции по маршрутам 1-1, 2-4 и 4-2. В результате был также получен оптимальный план перевозок, суммарные затраты для которого составили 7040 тыс. руб. Таким образом, можно видеть, что дополнительные ограничения на пропускную способность ведут к кардинальному изменению плана перевозок и увеличению суммарных затрат. | |||||||||||||||||||||||||||||||||||||||||||||||||
