ОИТ. Контрольная работа. Основы инфокоммуникационных технологий

• Название: Основы инфокоммуникационных технологий
• Дата: 04.12.2021
• Размер: 369.39 Kb.
• Имя файла: Контрольная работа.docx
• Тип: Курсовая; #291274

Федеральное агентство связи

федеральное государственное бюджетное образовательное учреждение

высшего образования

«Сибирский государственный университет телекоммуникаций и

информатики»

(СибГУТИ)

11.03.02 Инфокоммуникационные технологии и системы связи,

профиль Сети связи и системы коммутации

(заочная форма обучения)

Курсовая работа

по дисциплине «Основы инфокоммуникационных технологий»
Выполнил:

студент ФАЭС,

гр. ЗБТ-01 /

«__»_________ 2020 г. (подпись)
Проверил:

доц. каф. ПДСиМ /

«__»_________ 2017 г. (подпись)

Новосибирск 2020

Содержание

1.1 Формирование рисунка. 5

1.2 Определение алфавита дискретного источника 5

1.3 Определение количества информации 6

Количество информации в изображении можно измерить. Для этого изображение разбивают на отдельные маленькие фрагменты (пиксели). Каждому пикселю, формирующему изображение, назначается определенный цвет. Система растровых изображений использует RGB матрицу, т.е. три цвета: красный, зеленый и синий. Цвет каждого пикселя зависит от яркости этих цветов. Этот процесс называют пространственной дискретизацией изображения. Изображение, сформированное таким способом, называют растровым. 7

Качество такого изображения зависит от двух параметров- количество пикселей и количество цветов в палитре. 7

С количеством цветов в палитре связана глубина цвета. Чем больше цветов в палитре, тем большее количество информации несет в себе один пиксель. 7

Для кодирования цветов в рисунке применяется двоичный код. Для этого используем формулу Хартли (Формула 1): 7

7

1.4 Кодирование изображения 8

2.1 Блок – схема и программа генерации массива. 12

2.2 Генерация массивов функцией rbinom 15

2.3 Визуализация массива на оси времени 17

3.1 Программы и визуализация АМ, ЧМ и ФМ модуляторов. 18

Рисунок 3.5 – блок – схема Фазового модулятора 23

Напишем программу фазового модулятора: 23

23

23

Начертим график Фазовой модуляции: 24

Рисунок 3.6 – график ФМ 24

3.2 Использование функции rnorm 24

Используем функцию генерации случайной величины, распределенной про нормальному закону rnorm(L,m,). 24

rnorm(L,m,ϭ) – вектор L независимых случайных чисел, каждое из которых имеет нормальное распределение . 24

Нормальное распределение, также называемое распределением Гаусса-Лапласа- распределение вероятностей, которое в одномерном случае задаётся функцией плотности вероятности. 25

Добавим к каждому отсчёту модулированного сигнала случайную вели-чину генератора rnorm(1,0,ϭ) и выведем на графике. 25

Добавим шум к амплитудной модуляции: 25

25

25

25

Рисунок 3.7 – Сигнал АМ с шумом 25

Добавим шум к частотной модуляции: 25

26

Рисунок 3.7 – Сигнал ЧМ с шумом 26

Добавим шум к фазовой модуляции: 26

Рисунок – 3.8 – Сигнал ФМ с шумом 27

Вывод: в реальной жизни передать какой-либо сигнал или сообщение без помех практически невозможно, потому что на качество передачи влияет множество факторов. В итоге сигнал искажается и усложняется процесс приема сообщения. Использование шума в модуляции приближает ее к реальным условиям. 27

В результате выполнения работы решен ряд задач, которые имеющий отношение к телекоммуникационным системам, а именно 28

– определено количество информации произвольного рисунка, 28

– исследованы возможности MathCad, 28

– сформирован двоичный массив с желаемыми вероятностными параметра-ми, 28

– исследованы различные виды модуляций. 28

Введение
Технология передачи информации, возможно, в большей степени, чем любые другие технологии, оказывает влияние на формирование структуры мирового сообщества. Возможность доступа к важнейшим событиям, происходящим в мире, свидетельствует о могуществе сетей передачи данных, обеспечивающих мгновенную доставку неподверженной цензуре информации широкой мировой аудитории.

Благодаря возникновению и развитию сетей передачи данных появился новый, высокоэффективный способ взаимодействия между людьми. Первоначально сети использовались главным образом для научных исследований, но затем они стали проникать буквально во все области человеческой деятельности. При этом большинство сетей существовало совершенно независимо друг от друга, решая конкретные задачи для конкретных групп пользователей. В соответствии с этими задачами выбирались те или иные сетевые технологии и аппаратное обеспечение. Построить универсальную физическую сеть мирового масштаба из однотипной аппаратуры просто невозможно, поскольку такая сеть не могла бы удовлетворять потребности всех ее потенциальных пользователей. Одним нужна высокоскоростная сеть для соединения машин в пределах здания, а другим – надежные коммуникации между компьютерами, разнесенными на сотни километров. Тогда возникла идея объединить множество физических сетей в единую глобальную сеть, в которой использовались бы как соединения на физическом уровне, так и новый набор специальных "соглашений" или протоколов. Эта технология, получившая название internet, должна была позволить компьютерам "общаться" друг с другом независимо от того, к какой сети и каким образом они подсоединены.

Когда возникла задача создания сетей передачи данных для ЭВМ, естественным, прежде всего, было обращение к столетнему опыту работы с телеграфными сетями. Так, опыт работы с телеграфными сетями с промежуточным накоплением (переприем телеграмм с переносом перфоленты) пригодился при создании сетей передачи данных с коммутацией сообщений, а с сетями абонентского телеграфа – для создания сетей передачи данных с коммутацией каналов. Важную роль в развитии сетей передачи данных сыграл научно-технический прогресс. Он позволил в течение сравнительно небольшого периода времени перейти от бумажных перфолент и перфокарт к магнитным лентам, а затем к магнитным дискам, полупроводниковым и оптическим запоминающим устройствам.

Одновременно огромный скачок произошел в технике защиты передачи от помех. От простых способов обнаружения ошибок путем проверки перфоленты на четность числа пробитых в ней отверстий удалось перейти к высоконадежным кодам не только обнаруживающим, но и исправляющим ошибки. Самое же главное, была создана микроэлектронная база. Она позволила сделать сложную аппаратуру компактной и экономичной по расходу электроэнергии. Все это открыло возможности построения технических средств передачи с огромной скоростью и ознаменовало наступление новой эпохи развития документальной связи.

Целью работы является решение задач, имеющие отношение к телкоммуникационным системам.

Работа состоит из следующих задач:

– определение количества информации,

– исследование возможностей MathCad,

– генерация двоичного массива с желаемыми вероятностными параметрами,

– исследование различных видов модуляций
Задание 1

1.1 Формирование рисунка.

Задача состоит в том, чтобы самостоятельно сформировать рисунок, состоящий из 600 или более точек из четырех или более цветов.

При помощи стандартного приложения Windows «Paint» был сформирован рисунок размерами 30х30 точек из 8 различных цветов (рис.1).


Рисунок 1

Рисунок состоит из 900 точек(пикселей) и имеет 8 цветов (Таблица 1)

Таблица 1

Цвет	Размер	Количество точек
Желтый	10х10	100
Оранжевый	10х10	100
Красный	10х10	100
Пурпурный	10х10	100
Фиолетовый	10х10	100
Синий	10х10	100
Голубой	10х10	100
Зеленый	10х20	200

1.2 Определение алфавита дискретного источника

Под дискретным понимается источник, который в каждую единицу времени порождает один символ x_i из дискретного множества А = {a₁, a₂, ..., a_k}, называемого алфавитом источника, где k – размер алфавита. Источник, с точки зрения теории информации, считается заданным полностью, если известен не только алфавит источника, но и есть его модель, позволяющая вычислить вероятность любой последовательности символов в любой момент времени.

В сформированном рисунке 8 цветов.

Тогда размер источника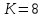

1.3 Определение количества информации

Количество информации в изображении можно измерить. Для этого изображение разбивают на отдельные маленькие фрагменты (пиксели). Каждому пикселю, формирующему изображение, назначается определенный цвет. Система растровых изображений использует RGB матрицу, т.е. три цвета: красный, зеленый и синий. Цвет каждого пикселя зависит от яркости этих цветов. Этот процесс называют пространственной дискретизацией изображения. Изображение, сформированное таким способом, называют растровым.

Качество такого изображения зависит от двух параметров- количество пикселей и количество цветов в палитре.

С количеством цветов в палитре связана глубина цвета. Чем больше цветов в палитре, тем большее количество информации несет в себе один пиксель.

Для кодирования цветов в рисунке применяется двоичный код. Для этого используем формулу Хартли (Формула 1):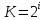



где N – Количество цветов в палитре / мощность алфавита

i – глубина цвета / длина двоичного кода, который используется для кодирования цвета пикселя.

Согласно формуле, составляем таблицу 2:

Таблица 2

Количество цветов в палитре	2	4	8	16	32	64	128	256	65536	16.7 млн.
Глубина цвета / размер пикселя	1	2	3	4	5	6	7	8	16	24

Человеческий глаз различает примерно 16,7 млн цветов. Поэтому максимальный размер пикселя, который используется при кодировании растровых изображений равен 24 бита.

Исходя из формулы Хартли и таблицы 2, определяем, что количество информации, приходящиеся на одну точку каждого цвета изображения в задании ровна 3 бита.

Проверим полученные данные формулой определения количества информации для равновероятностных событий: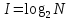



где I – количество информации,

N – количество возможных оттенков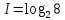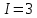



Определим общее количество информации в рисунке. Для этого воспользуемся формулой: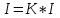



где I – общее количество информации

K – Количество пикселей / символов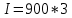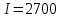



бит

Определим среднее количество информации, приходящиеся на одну точку в рисунке:

Среднее количество информации H, которое приходится на один символ источника сообщений можно найти по формуле: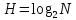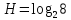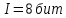

1.4 Кодирование изображения

Закодируем изображение равномерным двоичным кодом.

Равномерный код – код в котором длина всех кодовых комбинаций (кодовых слов) одинакова. Для этого воспользуемся таблицей 3 составленной ранее:

Таблица 3

Цвет	Код
Желтый	000
Оранжевый	001
Красный	010
Пурпурный	011
Фиолетовый	101
Синий	110
Голубой	100
Зеленый	111

Исходя из таблицы 3 видим, что для кодирования цвета одного пикселя потребовалось 3 двоичных элемента.

Определим среднее количество информации, приходящееся на один двоичный элемент при равномерном кодировании, при помощи формулы: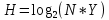



где Y – количество бит для представления оттенка,

N – количество возможных оттенков/цветов.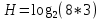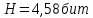




Закодируем рисунок неравномерным двоичным кодом.

Неравномерный код — это код, в котором кодовые слова имеют различную длину.

Чтобы была возможность однозначно декодировать сообщение при кодировании неравномерным двоичным кодом, необходимо соблюдение условия Фано – никакое кодовое слово не совпадает с началом другого кодового слова. Для этого используем бинарное ориентированное дерево:

Рисунок 2 - бинарное ориентированное дерево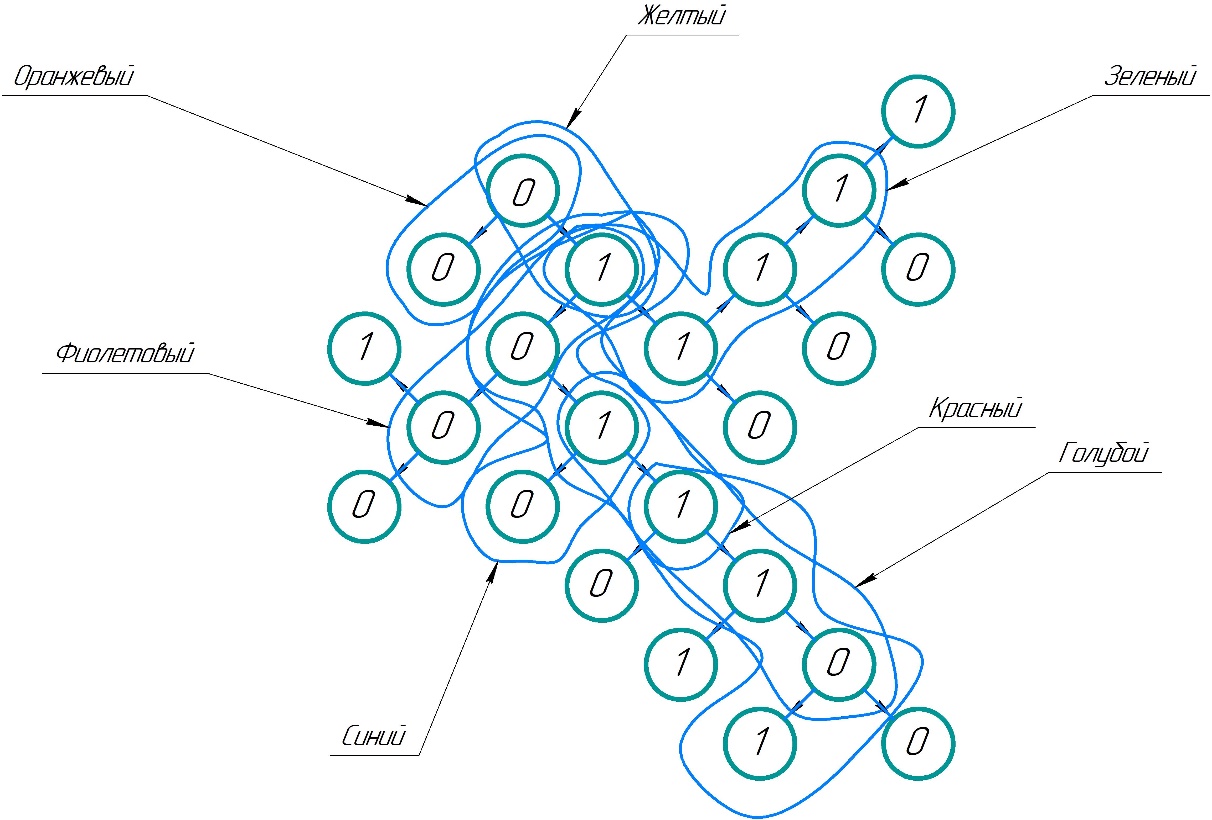



Составим таблицу неравномерного двоичного кода:

Цвет	Код
Желтый	01
Оранжевый	00
Красный	1011
Пурпурный	1101
Фиолетовый	100
Синий	1010
Голубой	1110
Зеленый	1111

Определить среднюю длину кодовой комбинации. Из таблицы видно, что

- один элемент закодирован тремя битами;

- два элемента закодированы двумя битами;

- пять элементов закодированы четырьмя битами;

Средняя длина определяется как среднее арифметическое с весовыми коэффициентами: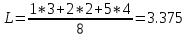

бит

Таким образом, для неравномерного кодирования достаточно примерно 3-х бит.

Определим среднее количество информации, приходящееся на один двоичный элемент при неравномерном кодировании: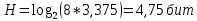



Вывод: при неравномерном кодировании рисунка размером 30х30 точек составленного из 8 цветов избыточность кодирования незначительно изменяется: всего на 0.17 бита.

Задание 2

Цель задания научиться составлять блок – схемы, составлять программу генерации массивов с разной длиной и заданной вероятностью появления единиц. Сравнить результаты при использовании функции rbinom.

2.1 Блок – схема и программа генерации массива.

Массив-структура данных в виде набора компонентов (элементов массива), расположенных в памяти непосредственно друг за другом.

Построим блок-схему генерации двоичного массива (рисунок 2.1)
Начало






N,p






i=0 .. n-1






Rnd(1)>p
0 1

X_i = 1

X_i = 0







X(n,p)







Конец

Рисунок 2.1 – блок – схема программы генерации массива.

Напишем программу генерации двоичного массива заданной длины с желаемой вероятностью появления единиц. Для написания программы будем использовать приложение Mathcad 15.




Рисунок 2.2 - программа генерации двоичного массива заданной длины с желаемой вероятностью появления единиц.

где n – количество элементов массива,

p – вероятность появления единиц.

n=10; 100; 1000,

p = 0,2

Проверим частоту появления единиц при длине массива n = 10:












Частота появления единиц при заданных параметрах равна 0.3

Проверим частоту появления единиц при длине массива n = 100:











Частота появления единиц при заданных параметрах равна 0.27

Проверим частоту появления единиц при длине массива n = 1000:











Частота появления единиц при заданных параметрах равна 0.191

Вывод: при увеличении длины массива, увеличивается точность значения частоты появления единиц.

2.2 Генерация массивов функцией rbinom

Функция rbinom - возвращает вектор из m случайных чисел, имеющих биномиальное распределение с размером n и вероятностью успеха q.

Проверим частоту появления единиц при длине массива n = 10:
















Частота появления единиц при заданных параметрах равна 0.2.

Проверим частоту появления единиц при длине массива n = 100:
















Частота появления единиц при заданных параметрах равна 0,17.

Проверим частоту появления единиц при длине массива n = 1000:
















Частота появления единиц при заданных параметрах равна 0,209.

Вывод: при использовании функции rbinom и увеличении длины массива, точность значения частоты появления единиц так же увеличивается.

2.3 Визуализация массива на оси времени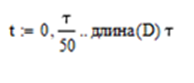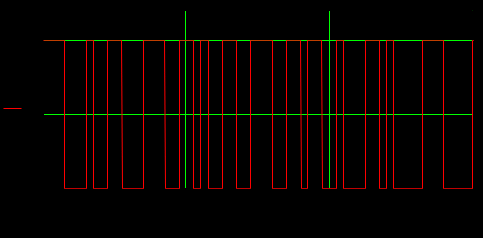

Рисунок 2.3 – График визуализации двоичного массива

Вывод: 1) Функция rbinom выполняет те же задачи, что и программа для генерации двоичного массива, а это значит: что гораздо рациональнее будет использование функции rbinom, ведь она более экономична и затрачивает меньше времени на написание.

2) При визуализации двоичного массива на оси времени, график принимает вид прямоугольного импульса.


Задание 3

3.1 Программы и визуализация АМ, ЧМ и ФМ модуляторов.

Модуляция – процесс изменения одного или нескольких параметров высокочастотного (несущего) колебания по закону низкочастотного(информационного) сигнала.

Модуляция переносит спектр исходного сигнала на частоту несущей или в любую точку диапазона и зеркально отображает.

Сгенерируем случайный двоичный массив из 12 элементов с вероятностью единицы (p=0,5):












Составим блок - схему для амплитудного модулятора(АМ):



НАЧАЛО






D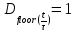







0 1





0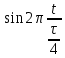







Конец

Рисунок 3.1 – Блок – схема амплитудного модулятора

Напишем программу для АМ: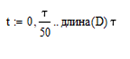







Построим график амплитудной модуляции: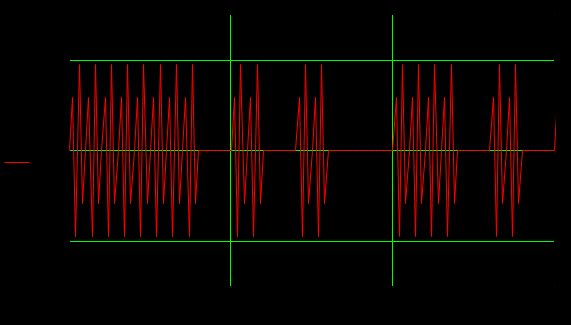


Рисунок 3.2 – График АМ

Начертим блок-схему для частотного модулятора(ЧМ):
НАЧАЛО





D







0 1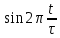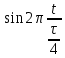














Конец


Рисунок 3.3 – Блок – схема для ЧМ


Напишем программу частотного модулятора: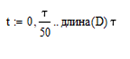









Построим график частотной модуляции: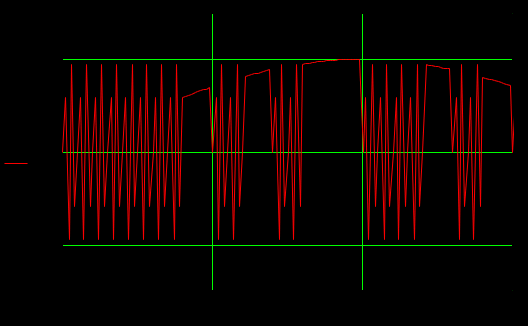



Рисунок 3.4 – График ЧМ

Начертим блок – схему фазового модулятора(ФЗ):


НАЧАЛО






D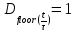







0 1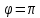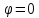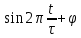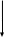




















Конец


Рисунок 3.5 – блок – схема Фазового модулятора

Напишем программу фазового модулятора: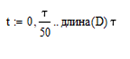









Начертим график Фазовой модуляции: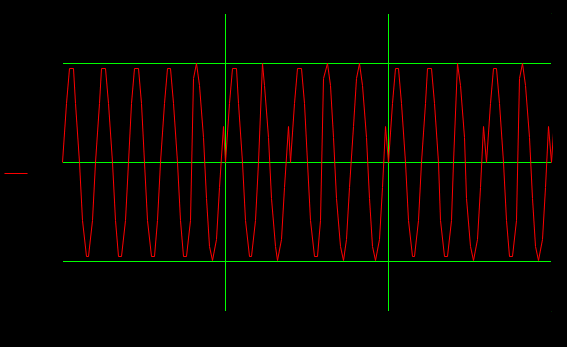



Рисунок 3.6 – график ФМ

3.2 Использование функции rnorm

Используем функцию генерации случайной величины, распределенной про нормальному закону rnorm(L,m, ).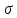

rnorm(L,m,ϭ) – вектор L независимых случайных чисел, каждое из которых имеет нормальное распределение .

Нормальное распределение, также называемое распределением Гаусса-Лапласа- распределение вероятностей, которое в одномерном случае задаётся функцией плотности вероятности.

Добавим к каждому отсчёту модулированного сигнала случайную вели-чину генератора rnorm(1,0,ϭ) и выведем на графике.

Добавим шум к амплитудной модуляции: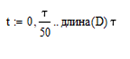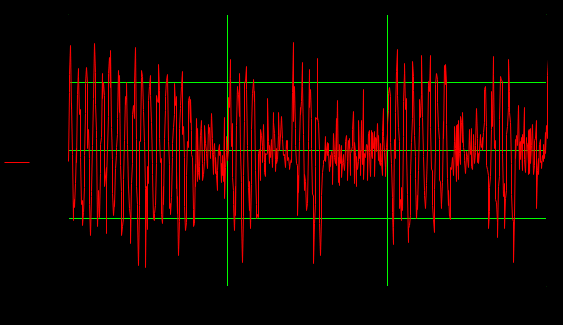

• 
  
  

Рисунок 3.7 – Сигнал АМ с шумом

Добавим шум к частотной модуляции: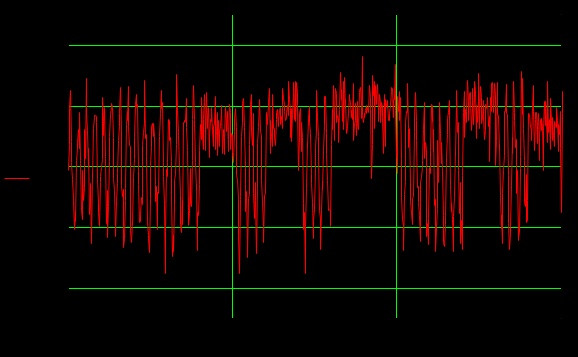

• 
  
  

Рисунок 3.7 – Сигнал ЧМ с шумом

Добавим шум к фазовой модуляции: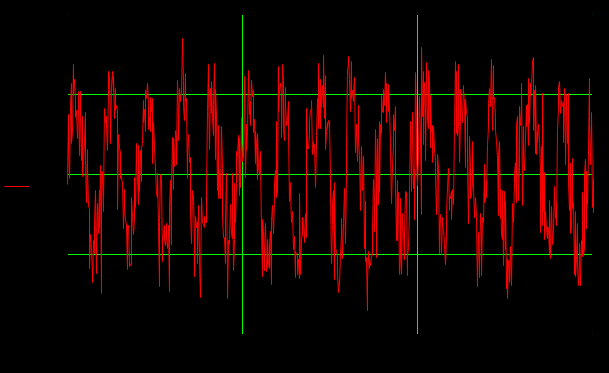








Рисунок – 3.8 – Сигнал ФМ с шумом

Вывод: в реальной жизни передать какой-либо сигнал или сообщение без помех практически невозможно, потому что на качество передачи влияет множество факторов. В итоге сигнал искажается и усложняется процесс приема сообщения. Использование шума в модуляции приближает ее к реальным условиям.


Заключение
В результате выполнения работы решен ряд задач, которые имеющий отношение к телекоммуникационным системам, а именно

– определено количество информации произвольного рисунка,

– исследованы возможности MathCad,

– сформирован двоичный массив с желаемыми вероятностными параметра-ми,

– исследованы различные виды модуляций.

Библиография

1. 
   ГОСТ Р 50922-96. Защита информации. Основные термины и определения. – Введ. 1997-07-01. – М.: Госстандарт России, 1996. – 17 с.
   
2. 
   Гольдштейн, Б.С. Сети связи: учебник / Б.С. Гольдштейн, Н.А. Соколов, Г.Г. Яновский. – СПб.: БХВ-Петербург, 2010. – 399с.
   
3. 
   Роговский, Е.А. Кибербезопасность: экономические риски и эффективность / Е.А. Роговский, М.Е. Соколова // США – Канада: экономика, политика, культура. – 2008. – № 4. – С. 83-91.
   
4. 
   Никитович, Н. Онлайн-банкинг: защиты много не бывает / Н. Никитович // Information Security/ Информационная безопасность – 2012. –№ 5. – URL: http://www.itsec.ru/articles2/Inf_security/onlayn-banking-zaschity-mnogo-ne-byvaet/ (дата обращения: 12.12.13).