Основы логического и функционального программирования.prn. Основы логического и функционального программирования
 Скачать 410 Kb. Скачать 410 Kb.
|
|
powerful (tiger) – цель, которая успешно доказана. В данном дереве целей две цели: middle (Animal) и strong (tiger), находящиеся в листьевых вершинах, и обе они доказаны.  Управление поиском с возвратом: предикаты ! и fail Управление поиском с возвратом заключается в решении двух задач: включении поиска с возвратом при его отсутствии, и отключении поиска с возвратом при его наличии. Для решения этих задач используются два стандартных предиката: предикат fail, включающий поиск с возвратом. предикат ! (этот предикат еще называют «отсечение»), предотвращающий поиск с возвратом. Рассмотрим, как работает предикат fail. Для начала следует напомнить, что поиск с возвратом начинает свою работу только в том случае, если не удается доказать какую-либо цель. Поэтому действует предикат fail очень просто – цель с использованием данного предиката НИКОГДА не доказывается, а, следовательно, всегда включается поиск с возвратом. Для получения такого же эффекта можно записать, например, вот такую цель: 2=3. Эффект будет абсолютно тем же самым. Предикат fail используется в тех случаях, когда в программе есть внутренняя цель, и необходимо позаботиться о нахождении всех возможных решений. Рассмотрим простой пример: вывод названий всех стран, перечисленных в фактах. PREDICATES country (string) CLAUSES country (“Финляндия”). country (“Швеция”). country (“Норвегия”). print:- country (Country_name), write (Country_name), nl. GOAL print. Результатом работы программы будет вывод только названия первой страны из перечня фактов – Финляндии. Произойдет это из-за того, что при использовании внутренней цели находится только первое решение задачи. Для того чтобы в процессе выполнения программы был выведен полный перечень названий стран, необходимо, чтобы цель country (Country_name) была передоказана столько раз, сколько имеется фактов в секции CLAUSES. Эта цель достигается очень просто. Предложение для предиката print нужно лишь переписать следующим образом: print:- country (Country_name), write (Country_name), nl, fail. В таком случае данное правило будет работать следующим образом: первый раз цель country (Country_name) будет успешно доказана с помощью факта country (“Финляндия”). и переменная Country_name будет конкретизирована значением “Финляндия”. Затем будет выведено значение переменной Country_name и наступит черед цели fail, которая никогда не доказывается. Естественно, будет инициализирован поиск с возвратом, и возврат будет выполнен к ближайшей цели, которую можно передоказать. (Следует отметить, что ближайшей считается цель, встреченная при возврате, то есть при движении справа налево.) Эта цель – country (Country_name). Так как заработал поиск с возвратом, переменная Country_name теряет свое значение, и ничто не препятствует успешному передоказательству цели country (Country_name) фактом country (“Швеция”). Подобные действия будут повторяться до тех пор, пока не будут исчерпаны все факты, используемые для доказательства. В результате будет выведен список всех стран, то есть программа выполнит те действия, которых от нее ждали. Однако следует сделать небольшое, но важное замечание. Несмотря на то, что программа выполнила все ожидаемые действия, в итоге выполнения программы завершится с неуспехом, поскольку цель print из секции GOAL доказана не будет. Недоказательство цели print произойдет вот по какой причине. Когда цель country (Country_name) будет в последний раз успешно доказана фактом country (“Норвегия”). в действие вновь вступает цель fail. Но передоказать цель country (Country_name) более нельзя, все факты исчерпаны и, так как не удалось доказать цель в теле правила и головная цель правила считается недоказанной, следовательно будет считаться недоказанной цель print из секции GOAL. Избежать этого изъяна в работе программы очень легко, следует всего лишь добавить еще одно предложение для предиката print. Следующий вариант примера будет выполнять все необходимые действия, и выполнение программы будет завершаться с успехом. PREDICATES country (string) CLAUSES country (“Финляндия”). country (“Швеция”). country (“Норвегия”). print:- country (Country_name), write (Country_name), nl, fail. print. GOAL print. В данном примере наличие второго предложения для предиката print создает еще одну точку возврата. Когда цель fail в очередной раз своим недоказательством включает поиск с возвратом, передоказать цель country (Country_name) более нельзя, все факты исчерпаны, вот тогда поиск с возвратом и возвращается к передоказательству цели print, что с успехом делается с помощью второго предложения для предиката print. Еще один пример, показывающий, как можно управлять поиском с возвратом без предиката fail. В приведенном примере выполняется вывод положительных чисел до первого встреченного отрицательного числа. В этом случае работа программы прекращается. PREDICATES number (integer) output CLAUSES number (2). number (1). number (0). number (-1). number (-2). output:- number (Positive_number), write (Positive_number), nl, Positive_number<0. output. GOAL output. В данном случае цель Positive_number<0 играет роль, если так можно выразиться, условного предиката fail. Пока цель number (Positive_number) будет доказываться фактами, содержащими положительные числа, цель Positive_number<0 доказываться не будет, и, сдедовательно, будет работать поиск с возвратом. Как только переменная Positive_number будет конкретизирована значением –1, цель Positive_number<0 будет успешно доказана, завершится успехом доказательство всего правила и цели output в секции GOAL. В этом примере второе предложение для предиката output требуется только на тот случай, если бы все факты number содержали бы только положительные числа. Еще одно средство для управления поиском с возвратом – это стандартный предикат ! (отсечение). Действие этого предиката прямо противоположно действию предиката fail. Если предикат fail всегда включает поиск с возвратом, то отсечение поиск с возвратом прекращает. Рассмотрим, как работает отсечение, на примере. Пусть имеется набор фактов, описывающих некоторые числа. PREDICATES tens (string) ones (string) numbers CLAUSES tens ("двадцать"). tens ("тридцать"). ones ("два"). ones ("три"). numbers:- tens (Tens_number), ones(Ones_number), write (Tens_number, " ", Ones_number), nl, fail. numbers. GOAL numbers. Результатом работы программы будет вывод следующих строк: двадцать два двадцать три тридцать два тридцать три (выполнение программы завершится с успехом) В данном случае в программе будет две точки возврата, которые и дадут этот эффект. Вместо подробного описания работы программы ниже дается трассировка (с некоторыми несущественными сокращениями), из которой становится ясной логика работы программы. Следует заметить, что выполнение программы завершится с успехом. CALL: numbers () CALL: tens (_) RETURN: *tens ("двадцать") CALL: ones (_) RETURN: *ones ("два") write ("двадцать", " ", "два") REDO: ones (_) RETURN: ones ("три") write ("двадцать", " ", "три") REDO: tens (_) RETURN: tens ("тридцать") CALL: ones (_) RETURN: *ones ("два") write ("тридцать", " ", "два") REDO: ones (_) RETURN: ones ("три") write ("тридцать", " ", "три") REDO: numbers () RETURN: numbers () Если теперь добавить в правило вывода отсечение, numbers:- tens (Tens_number), !, ones (Ones_number), write (Tens_number, " ", Ones_number), nl, fail. то это существенно изменит результат работы программы: двадцать два двадцать три (выполнение программы завершится с неуспехом) Почему отсечение произвело такой эффект? Рассмотрим, как работает отсечение. Когда выполняется последовательное доказательство целей слева направо, то цель ! (отсечение) доказывается всегда и при этом выполняется еще одно очень важное действие – отсечение уничтожает все точки возврата, которые остались слева от отсечения. Следовательно, когда цель ! была успешно доказана, точка возврата для цели tens (Tens_number) была уничтожена, а с точкой возврата для цели ones (Ones_number) ничего не произошло. Когда предикат fail инициализировал поиск с возвратом, «в живых» осталась только одна точка возврата, для цели ones (Ones_number), то есть только для этой цели перебирались все возможные решения. Другими словами, после того, как доказательство целей миновало отсечение, поиск с возвратом возможен только справа от отсечения (нужно отметить, что, до тех пор, пока цель отсечение не доказана, поиск с возвратом возможен и слева от цели !). Пример трассировки для второго варианта правила. CALL: numbers () CALL: tens (_) RETURN: *tens ("двадцать") CALL: ones (_) RETURN: *ones ("два") write ("двадцать", " ", "два") REDO: ones (_) RETURN: ones ("три") write ("двадцать", " ", "три") В целом выполнение программы завершается с неуспехом, так как отсечение уничтожило не только возможность возврата к передоказательству цели tens (Tens_number), но и цели numbers. Перестановка отсечения в правиле будет существенно изменять результаты работы программы, и при наличии отсечения приведенный пример всегда будет завершаться с неуспехом. numbers:- tens (Number1), ones (Number2), !, write (Number1, " ", Number2), nl, fail. двадцать два (выполнение программы завершится с неуспехом) numbers:- !, tens (Number1), ones (Number2), write (Number1, " ", Number2), nl, fail. двадцать два двадцать три тридцать два тридцать три (выполнение программы завершится с неуспехом) Отсечение весьма полезно при организации ветвления с помощью нескольких правил с одной и той же целью в заголовке правила. Пример программы, которая проверяет, делится ли введенное число нацело на 2, на 3 или на 5. PREDICATES division (integer) start (string) CLAUSES division (N):- N mod 2 = 0, !, write (N, “делится на 2 без остатка.”), nl. division (N):- N mod 3 = 0, !, write (N, “делится на 3 без остатка.”), nl. division (N):- N mod 5 = 0, !, write (N, “делится на 3 без остатка.”), nl. division (_):- write (“Ваше число не делится нацело ни на 2, ни на 3, ни на 5!!!”). GOAL write (“Ваше число? ”), readint (Number), division (Number). В рассмотренном примере отсечение убирает совершенно ненужные точки возврата. Предположим, пользователь ввел число 1023. В этом случае в первом правиле для предиката division условие N mod 2 = 0 доказано не будет, следовательно, будет выполнен откат ко второму правилу. Препятствий для отката нет, так как отсечение в первом правиле не сработало. Во втором правиле условие N mod 3 = 0 успешно доказывается, и в этом случае доказательство проходит через отсечение. Как уже упоминалось, отсечение всегда доказывается с успехом, и будут уничтожены все точки возврата, проставленные к моменту доказательства цели !, оказавшиеся совершенно ненужными. Действительно, ведь если условие N mod 3 = 0 верно, а то, что N не делится нацело на 2, было проверено с помощью первого правила, третье и четвертое правила для предиката division точно не понадобится, то есть и не нужно сохранять бесполезную точку возврата. Если при написании программы есть возможность выносить проверку некоторого условия непосредственно в заголовок правила, лучше это сделать. Например, программа, проверяющая, является ли введенное число равным 1, 2 или 3, может быть написана следующим образом: … choice (N):- N=1, !, write (“Это единица.”). choice (N):- N=2, !, write (“Это двойка.”). choice (N):- N=3, !, write (“Это тройка.”). choice (N):- write (“Это не единица, не двойка, не тройка!!!”). … Более кратко правила можно записать с проверкой значения N не отдельным условием, а непосредственно в заголовке правила: … choice (1):- !, write (“Это единица.”). choice (2):- !, write (“Это двойка.”). choice (3):- !, write (“Это тройка.”). choice (_):- write (“Это не единица, не двойка, не тройка!!!”). … Анонимная переменная в заголовке последнего правила говорит о том, что значение переменной роли не играет. Действительно, если дело дошло до последнего правила, значит, значение переменной не равно 1, 2 или 3. Всегда следует убирать ненужные точки возврата как можно раньше. Итак, поиск с возвратом возможен только в случае, если в предложении есть цели, которые можно передоказать. Как же быть, если поиск с возвратом необходим для решения задачи, но нет целей, которые можно передоказывать? В такой ситуации приходиться создавать точку возврата искусственно, используя специальный предикат, для которого должны быть определены два предложения. Цель, записанная с использованием данного предиката, должна соответствовать двум условиям: не выполнять никаких видимых действий и ВСЕГДА генерировать точку возврата. Такой специальный предикат определяется следующим образом (предикат не является стандартным и его имя может быть выбрано совершенно произвольно): repeat. repeat:- repeat. Рассмотрим пример: вывод приглашения «>», ввод с клавиатуры строки и вывод ее на экран до тех пор, пока не будет введена строка stop. PREDICATES repeat echo CLAUSES repeat. repeat:- repeat. echo:- repeat, write (“> ”), readln (String), write (String), nl, String=”stop”. GOAL echo. Если написать правило вывода без цели repeat, echo:- write (“> ”), readln (String), write (String), nl, String=”stop”. будет выполнен ввод и вывод только первой и единственной введенной строки, неравной “stop”. Действительно, после ввода и вывода строки будет выполнена проверка String=”stop”, которая завершится неуспехом, что приведет к включению поиска с возвратом, но ни одну из целей в правиле передоказать нельзя (точки возврата не были проставлены), поэтому выполнение программы завершится неуспехом. Рассмотрим вариант правила с использованием цели repeat. При первом доказательстве цели repeat она успешно доказывается с помощью факта repeat. , при этом проставляется точка возврата, так что, если в дальнейшем не будет доказана какая-либо цель, можно будет вернуться к цели repeat и передоказать ее с помощью правила вывода repeat:- repeat. Далее выполняется успешное последовательное доказательство всех целей, вплоть до цели String=”stop”, которая, в случае, если была введена строка, неравная ”stop”, не доказывается. Как известно, недоказательство некоторой цели приводит к включению поиска с возвратом. В данном примере цели write (“> ”), readln (String), write (String) и nl передоказать нельзя, предикат repeat же определен таким образом, что всегда может быть передоказан. Цель repeat успешно передоказывается (вновь с генерацией точки возврата) и возобновляется естественный порядок доказательства целей, слева направо. Таким образом, организовываются повторяющиеся действия с помощью поиска с возвратом в том случае, когда исходно не было целей, дающих точку возврата. Рекурсия Рекурсия – это второе средство для организации повторяющихся действий в Prolog’е. Рекурсивная процедура – это процедура, вызывающая сама себя до тех пор, пока не будет соблюдено некоторое условие, которое остановит рекурсию. Такое условие называют граничным. Рекурсия – хороший способ для решения задач, содержащих в себе подзадачу такого же типа. Пример рекурсии: найти факториал n!. Задача нахождения значения факториала n! очень хорошо решается с помощью рекурсии, поскольку может быть сведена к решению аналогичной подзадачи, которая, в свою очередь, сводится к решению аналогичной подподзадачи и т.д. Действительно, чтобы найти значение факториала n!, можно найти значение факториала (n–1)! и умножить найденное значения на n. Для нахождения значения факториала (n–1)! можно пойти по уже известному пути – найти значение факториала (n–2)! и умножить найденное значения на n–1. Так можно действовать до тех пор, пока не доберемся до нахождения значения факториала (n–n)! или другими словами, факториала 0!. Значение факториала 0! известно – это 1. Вот это и будет граничное условие, которое позволит остановить рекурсию. Все, что теперь остается – это умножить полученную 1 на (n-(n-1)), затем на (n-(n-2)) и т.д. столько раз, сколько было рекурсивных вызовов. Результат n! получен. Вот как выглядит программа, которая проделывает вычисление n! (нужно заметить, что предложения Prolog-программы достаточно точно повторяют формулировку задачи на естественном языке). PREDICATES factorial (integer, integer) CLAUSES %факториал 0! равен 1 factorial (0, 1):- !. %факториал n! равен факториалу (n–1)!, умноженному на n factorial (N, Factorial_N):- M=N–1, factorial (M, Factorial_M), Factorial_N=Factorial_M*N. GOAL write (“Для какого числа Вы хотите найти факториал? ”), readint (Number), factorial (Number, Result), write (Number, “!=”, Result). Результат работы программы: 3!=6 Каким же образом работает программа? Выполнение программы начинается с последовательного доказательства целей, записанных в секции GOAL. Доказательство первых двух целей обеспечивает вывод подсказки и ввод значения Number (пусть будет введено значение 3). Эти цели успешно доказываются и очередь доходит до цели, собственно обеспечивающей вычисление факториала. С учетом того, что переменная Number уже конкретизирована значением 3, цель, которую нужно доказать, будет иметь вид factorial (3, Result). Для доказательства поставленной цели будет выполнен последовательный перебор предложений и определено, что для доказательства можно использовать второе предложение factorial (N, Factorial_N):- M=N–1, factorial (M, Factorial_M), Factorial_N=Factorial_M*N. Цель factorial (Number, Result) сопоставляется с заголовком правила factorial (N, Factorial_N) и выполняется унификация, в результате которой переменные Number и N, Result и Factorial_N становятся сцепленными, что приводит к тому, что переменная N также получает значение 3. Чтобы заголовок правила считался доказанным, необходимо, чтобы были доказаны все хвостовые цели правила вывода, то есть последовательно нужно доказать цели M=N–1, factorial (M, Factorial_M) и Factorial_N=Factorial_M*N. Первая цель доказывается успешно: 2=3–1, переменная M конкретизируется значением, равным 2. Доказательство следующей цели factorial (2, Factorial_M) приводит в действие рекурсию. Цель factorial (2, Factorial_M) вновь сопоставляется с заголовком того же самого правила factorial (N, Factorial_N), и теперь переменные M и N, Factorial_M и Factorial_N также становятся сцепленными. Но только переменные, используемые в рекурсивном вызове, являются самостоятельными переменными, несмотря на то, что для них используются те же самые имена. Для того, чтобы различать переменные на различных уровнях рекурсии, к их именам будет добавляться апостроф, вот так – Factorial_M’. Следует отметить, что доказательство цели Factorial_N=Factorial_M*N пока откладывается до тех пор, пока не будет доказана цель factorial (2, Factorial_M). Поскольку в действие вступает рекурсия, все повторяется вновь: успешное доказательство цели 1=2–1, рекурсивный вызов factorial (1, Factorial_M’), отложенная цель Factorial_M=Factorial_M’*M. Далее: успешное доказательство цели 0=1–1, рекурсивный вызов factorial (0, Factorial_M’’). НО! вот теперь наступил момент для остановки рекурсии, поскольку впервые значение факториала уменьшилось до 0, то есть впервые для доказательства цели factorial (0, Factorial_M’’) используется первое правило и наконец-то первый раз рекурсивная цель factorial (0, Factorial_M’’) успешно доказывается фактом factorial (0, 1)! Это событие позволяет впервые пройти к доказательству цели Factorial_M’=Factorial_M’’*M’, которая на всех предыдущих уровнях рекурсии оставалась отложенной. Цель успешно доказывается 1=1*1. В самом последнем рекурсивном вызове впервые доказаны все три хвостовые цели правила, что позволяет вернуться в рекурсии на один уровень выше и считать доказанной цель factorial (1, 1). Теперь можно пройти к доказательству отложенной цели 2=1*2. И вновь – доказаны все три хвостовые цели правила на этом уровне рекурсии, что позволяет вернуться в рекурсии еще на один уровень выше и считать доказанной цель factorial (2, 2). Снова можно пройти к доказательству отложенной цели 6=2*3. Выполнение программы практически завершено, поскольку доказаны все три хвостовые цели на самом верхнем уровне рекурсии, что дает возможным считать доказанной головную цель правила factorial (3, 6), и, далее, доказанной цель из секции GOAL factorial (3, 6). На завершающем этапе успешно доказывается последняя цель из секции GOAL, которая выводит на экран полученный результат. Выполнение программы с успехом завершено. Обратите внимание, что результат рассчитывается в процессе возврата из рекурсивных вызовов и доказательства отложенных целей. В момент, когда рекурсия останавливается граничным условием, то есть при доказательстве цели factorial (0, Factorial_M’’) значение факториала равно 1 (factorial (0, 1)). Описание работы программы получилось достаточно громоздким, более наглядно работу программы можно представить в виде дерева целей.  Непременно нужно отметить очень важную роль отсечения в первом предложении программы. Видимых действий здесь отсечение не производит, если его убрать, то есть записать первое предложение как факт factorial (0, 1). результат работы программы останется тем же. В чем же тогда смысл отсечения в этом примере? Отсечение убирает совершенно ненужную точку возврата, которая в дальнейшем может доставить много хлопот, если на нее не обратить внимания и оставить. Это утверждение можно пояснить на примере. Выполнение программы начинается с попытки доказательства цели, например, factorial (3, Result). Для доказательства данной цели будет использовано второе правило вывода, так как в первом правиле нет совпадения по первому аргументу (3<>0), что приведет, естественно, к последовательному доказательству хвостовых подцелей правила. В процессе этого доказательства нужно будет доказать рекурсивную цель factorial (2, Factorial_M), что вновь приведет к использованию второго правила вывода (в действие вступает рекурсия), так как первое правило по прежнему не подходит для доказательства из-за несовпадения первого аргумента. Подобные действия будут продолжаться до тех пор, пока рекурсивная цель не примет вид factorial (0, Factorial_M’’). Вот теперь наступил ключевой момент! Впервые для доказательства рекурсивной цели будет использовано первое правило. При этом цель factorial (0, Factorial_M’’) будет успешно, с помощью первого правила, доказана, но при этом остается потенциальная возможность использовать для доказательства той же самой цели второе правило. Другими словами, будет поставлена точка возврата. Но никакого передоказательства в дальнейшем не потребуется! Значение 0! всегда равно 1!. Вот часть трассировки выполняемой программы для случая БЕЗ отсечения: factorial (0, 1). factorial (N, Factorial_N):- M=N–1, factorial (M, Factorial_M), Factorial_N=Factorial_M*N. … CALL: factorial (2, _) REDO: factorial (2, _) 1=1 CALL: factorial (1, _) REDO: factorial (1, _) 0=0 CALL: factorial (0, _) RETURN: *factorial (0, 1) вот он, ключевой момент! цель доказана, … но * говорит о том, что поставлена точка возврата Теперь часть трассировки выполняемой программы для случая С отсечением: factorial (0, 1):- !. factorial (N, Factorial_N):- M=N–1, factorial (M, Factorial_M), Factorial_N=Factorial_M*N. … CALL: factorial (2, _) REDO: factorial (2, _) 1=1 CALL: factorial (1, _) REDO: factorial (1, _) 0=0 CALL: factorial (0, _) RETURN: factorial (0, 1) цель доказана, … но точка возврата НЕ поставлена Каковы могут быть последствия, если точку возврата не убрать с помощью отсечения. Предположим, предикат factorial используется в каком-нибудь правиле вывода, например: … factorial (0, 1). factorial (N, Factorial_N):- M=N–1, factorial (M, Factorial_M), Factorial_N=Factorial_M*N. calculate (N, Res):- factorial (N, Res), Res<1000, !, write (“Все в порядке!”). calculate (_, _):- write (“Слишком большое число!”). … Что же произойдет, если будет рассчитываться, например, факториал 7! (7!=5040)? Цель factorial (N, Res) будет успешно доказана, но следующая цель Res<1000 доказана не будет, то есть начнется поиск с возвратом, который как известно, возвращается к ближайшей точке возврата. В данном примере эта точка оставлена в предикате factorial. То есть, вместо того, чтобы вывести сообщение “Слишком большое число!”, как задумал автор программы, программа проваливается в бесконечную рекурсию и выполнение программы прекращается из-за переполнения стека. Для иллюстрации вышесказанного приводится выдержка из трассировки: … CALL: calculate(7, _) CALL: factorial (7, _) FAIL: factorial (7, _) REDO: factorial (7, _) 6=6 CALL: factorial (6, _) FAIL: factorial (6, _) REDO: factorial (6, _) … REDO: factorial (1, _) 0=0 CALL: factorial (0, _) RETURN: *factorial (0,1) оставшаяся точка возврата 1=1 RETURN: factorial (1,1) … RETURN: factorial (6,720) 5040=5040 RETURN: factorial (7,5040) 5040<1000 FAIL: calculate(7, _) неудача, начинается поиск с возвратом REDO: factorial (0, _) а вот и последствия, возвращаемся и -1=-1 проваливаемся в бесконечную рекурсию CALL: factorial (-1, _) FAIL: factorial (-1, _) REDO: factorial (-1, _) -2=-2 CALL: factorial (-2, _) FAIL: factorial (-2, _) REDO: factorial (-2, _) -3=-3 CALL: factorial (-3, _) … Теперь, для сравнения, как все происходит, если точка возврата ликвидирована с помощью отсечения: … factorial (0, 1):- !. factorial (N, Factorial_N):- M=N–1, factorial (M, Factorial_M), Factorial_N=Factorial_M*N. calculate (N, Res):- factorial (N, Res), Res<1000, !, write (“Все в порядке!”). calculate (_, _):- write (“Слишком большое число!”). … Вновь пример трассировки: … REDO: factorial (1, _) 0=0 CALL: factorial (0, _) RETURN: factorial (0,1) точки возврата нет!!! 1=1 RETURN: factorial (1,1) … RETURN: factorial (6, 720) 5040=5040 RETURN: factorial (7, 5040) 5040<1000 FAIL: calculate (7, _) REDO: calculate (7, _) write("Слишком большое число!") работает, как и было задумано!!! … Вывод из всего вышеизложенного – никогда не оставлять ненужные точки возврата, убирая их с помощью отсечения. Если программа объемная, то достаточно сложно понять, куда выполняется откат и где оставлена лишняя точка возврата. Рассмотрим еще один пример рекурсивной программы. Поскольку в PDC Prologe’е нет стандартного предиката для возведения в степень, приходится эту операцию реализовывать самостоятельно. Для решения этой задачи также очень удобно использовать рекурсию, так как для того чтобы вычислить xn, можно вычислить x(n-1) и умножить полученный результат на x. Для вычисления x(n-1) воспользоваться тем же способом: вычислить x(n-2) и умножить полученный результат на x. Продолжать эти действия до тех пор, пока не придет черед вычисления x(n-n), что, как известно равно 1 (любое число в нулевой степени равно единице x0=1). Вот как это реализуется на Prolog’е: PREDICATES %первый аргумент – основание степени, второй – показатель степени, % третий – результат power (real, integer, real) CLAUSES %любое число в нулевой степени равно 1 power (_, 0, 1):- !. %xn=x(n–1)*x power (X, N, X_powerN):- M=N–1, power (M, X_powerM), Xpower_N=Xpower_M*X. GOAL write (“Основание степени? ”), readreal (X), write (“Показатель степени? ”), readint (N), power (X, N, Result), write (X, “ в степени ”, N“ =”, Result). Результат работы программы: 3 в степени 2=9 Как видно, рекурсивные задачи, решаемые с помощью Prolog’а, отличаются краткостью и приближенностью к естественному языку. Но таким образом организованная рекурсия имеет один, но существенный недостаток. При достаточно глубокой рекурсии переполняется стек вызовов, и выполнение программы аварийно завершается. Можно ли избежать такой ситуации? Да, это возможно, при специальным образом организованной рекурсии. Такая рекурсия называется хвостовой. Прежде чем перейти к рассмотрению хвостовой рекурсии, рассмотрим для начала следующий пример. Предположим, имеются некоторые абстрактные процедуры F1, F2, F3 и F4. Пусть в процессе выполнения процедуры F1 выполняется вызов процедуры F2, при выполнении которой, в свою очередь, вызывается процедура F3, которая, в свою очередь, вызывает F4. В этом случае стек вызовов будет выглядеть следующим образом:
Сохранять состояние вызывающей процедуры необходимо для того, чтобы продолжить ее выполнение после завершения вызова. Но, а если вызов процедур F2, F3 и F4 будет последним действием в вызывающих процедурах? Тогда можно не сохранять состояние вызывающей процедуры, так как в ней после завершения вызова больше ничего выполняться не будет. Можно хранить в стеке вызовов только состояние последней вызванной процедуры, другими словами подменять состояние бывшей процедуры состоянием новой процедуры.
То есть считать, что процедура F1 вызывает процедуру F4 непосредственно. В этом случае, не расходуется стек вызовов. Теперь перейдем к варианту с рекурсивными вызовами процедур. Пусть в процессе выполнения процедуры F1 выполняется вызов процедуры F2, при выполнении которой, в свою очередь, рекурсивно вызывается процедура F2, которая, в свою очередь, вновь рекурсивно вызывает саму себя, то есть опять вызывает F2. В этом случае стек вызовов будет хранить только состояние последнего рекурсивного вызова, то есть стек вновь не будет переполняться!
Выполнение таким образом организованной рекурсии не будет завершаться аварийно из-за переполнения стека, сколько бы ни было рекурсивных вызовов! Аварийное завершение по другим причинам, конечно, не исключается. Можно на практике убедиться, что это действительно так. Попробуйте запустить следующую программу и посмотреть, в течение какого времени она будет благополучно работать: PREDICATES tail_recursion CLAUSES %хвостовая рекурсия tail_recursion:- write (“*”), tail_recursion. GOAL tail_recursion. Теперь можно сформулировать условия, при соблюдении которых рекурсия в Prolog’е становится хвостовой, то есть не расходует стек при неограниченном количестве рекурсивных вызовов: рекурсивный вызов должен быть последней целью в хвостовой части правила вывода. перед рекурсивным вызовом не должно быть точек возврата (это условие хвостовой рекурсии специфично для Prolog’а). Если первое условие очевидно, то необходимость выполнения второго условия может быть, на первый взгляд, не совсем понятна. Чтобы рекурсия была хвостовой, необходимо, чтобы доказательство рекурсивного вызова было действительно последним действием в хвостовой части правила. А если до рекурсивного вызова имеется цель, которую можно передоказать, то есть имеется точка возврата? Тогда придется сохранять в стеке состояние вызывающего правила! Вдруг в дальнейшем, где-то в глубинах рекурсии какая-либо цель не будет доказана? Тогда будет включен поиск с возвратом к ближайшей точке возврата, для чего и нужно сохранять состояние в стеке соответствующего правила (чтобы знать, куда вернуться). Если соблюдение первого условия сложности не представляет (легко проконтролировать, чтобы рекурсивный вызов был последней целью в теле правила), то как быть уверенным в соблюдении второго условия, в отсутствии точек возврата до рекурсивного вызова? Соблюсти второе условие очень просто. Достаточно перед рекурсивным вызовом поставить отсечение. Только и всего! Конечно, использовать отсечение следует как можно раньше в теле правила, но, в крайнем случае, его можно использовать в качестве предпоследней цели (последняя цель, естественно, рекурсивный вызов) Примеры нехвостовой рекурсии и ее преобразования в хвостовую: %пример нехвостовой рекурсии PREDICATES counter (integer) CLAUSES counter (N):- write (“N=”, N), nl, New_N=N+1, counter (New_N), nl. GOAL counter (0). Естественно, приведенный пример не является примером хвостовой рекурсии, однако получить хвостовую рекурсию достаточно просто: нужно всего лишь убрать цель nl (переход на новую строчку) после рекурсивного вызова. %пример хвостовой рекурсии PREDICATES counter (integer) CLAUSES %выполнение программы аварийно завершится из-за переполнения %разрядной сетки для integer, но не из-за переполнения стека counter (N):- write (“N=”, N), nl, New_N=N+1, counter (New_N). GOAL counter (0). В рассмотренном примере соблюдены оба условия хвостовой рекурсии: рекурсивный вызов последний в теле правила и нет точек возврата перед рекурсивным вызовом. Действительно, цели write (“N=”, N), nl и New_N=N+1 передоказать нельзя, соответственно, нет и точки возврата. %пример нехвостовой рекурсии PREDICATES counter (integer) CLAUSES counter (N):- N>0, write (“N=”, N), nl, New_N=N–1, counter (New_N). counter (N):- write (“Отрицательное N=”, N). GOAL counter (1000). В приведенном примере рекурсия хвостовой не является из-за оставленной точки возврата. Пока N будет положительным, для доказательства рекурсивной подцели будет использоваться первое правило вывода, но ведь остается неиспользованным второе правило, что и дает точку возврата. Преобразовать нехвостовую рекурсию в хвостовую можно, убрав точку возврата с помощью отсечения. Первое правило нужно переписать следующим образом: counter (N):- N>0, !, write (“N=”, N), nl, New_N=N–1, counter (New_N). Если N – положительное число, второе правило заведомо не понадобится. %пример хвостовой рекурсии PREDICATES counter (integer) CLAUSES counter (N):- N>0, !, write (“N=”, N), nl, New_N=N–1, counter (New_N). counter (N):- write (“Отрицательное N=”, N). GOAL counter (1000). %пример нехвостовой рекурсии PREDICATES counter (integer) check (integer) CLAUSES counter (N):- check (N), write (“N=”, N), nl, New_N=N–1, counter (New_N). check (N):- N>0, write (“Положительное ”). check (_):- write (“Отрицательное ”). GOAL counter (1000). В приведенном примере рекурсия также хвостовой не является вновь из-за оставленной точки возврата. Пока N будет положительным, для доказательства рекурсивной подцели будет использоваться первое правило вывода для предиката check, но ведь остается неиспользованным второе правило для того же самого предиката, что и дает точку возврата. Преобразовать нехвостовую рекурсию в хвостовую можно, убрав точку возврата с помощью отсечения, как и в первом примере. Первое правило для предиката counter можно переписать следующим образом: counter (N):- check (N), !, write (“N=”, N), nl, New_N=N–1, counter (New_N). Но более правильно, с точки зрения хорошего стиля программирования на Prolog’е, точку возврата лучше убрать в предложении для предиката check. %пример хвостовой рекурсии PREDICATES counter (integer) check (integer) CLAUSES counter (N):- check (N), write (“N=”, N), nl, New_N=N–1, counter (New_N). check (N):- N>0, !, write (“Положительное ”). check (_):- write (“Отрицательное ”). GOAL counter (1000). Не всегда так легко и просто можно преобразовать нехвостовую рекурсию в хвостовую. Иногда для этого требуется полностью переписать программу. Рассмотрим уже известный пример вычисления факториала. Рекурсия в приведенном ранее примере, очевидно, хвостовой не является. Только с помощью применения отсечения добиться хвостовой рекурсии нельзя. Придется полностью преобразовать программу. Пример: вычисление n! с применением хвостовой рекурсии. PREDICATES factorial (integer, integer) factorial_aux (integer, integer, integer, integer) CLAUSES factorial (N, Factorial_N):- factorial_aux (N, Factorial_N, 1, 1). factorial_aux (N, Factorial_N, Counter, Product):- Counter<=N, !, New_Product=Product*Counter, New_Counter=Counter+1, factorial_aux (N, Factorial_N, New_Counter, New_Product). factorial_aux (_, Factorial_N, _, Factorial_N). GOAL write (“Для какого числа Вы хотите найти факториал? ”), readint (Number), factorial (Number, Result), write (Number, “!=”, Result). В данном случае при организации рекурсии были использованы вспомогательный предикат factorial_aux с четырьмя параметрами. Переменные N и Factorial_N служат для тех же целей, что и в примере с нехвостовой рекурсией, переменная N конкретизируется значением, для которого нужно вычислить факториал, Factorial_N – собственно полученный результат. Переменные Counter и Product – вспомогательные, Counter – счетчик рекурсивных вызовов, Product – постепенно накапливающийся результат. Рассмотрим более подробно работу программы. Единственное предложение для предиката factorial служит для того, чтобы перейти от предиката с двумя параметрами к вызову предиката с четырьмя параметрами. Первое предложение для предиката factorial_aux выполняет основные вычисления. При этом результат постепенно формируется при выполнении рекурсивных вызовов и достигает нужного значения в момент, когда текущий счетчик Counter становится больше значения N. В этот момент переменная Product конкретизируется значением готового результата, то есть в момент, когда рекурсия должна быть остановлена, значение факториала уже рассчитано. В приведенном примере результат готов в тот момент, когда условие Counter<=N более не выполняется (соответственно цель Counter<=N не доказывается), переменная Product конкретизируется значением рассчитанного факториала. Теперь необходимо передать полученное значение из четвертого параметра во второй. Для этого служит второе предложение для предиката factorial_aux. Цель Counter<=N не доказывается и выполняется поиск с возвратом ко второму предложению для предиката factorial_aux. Использование одноименных переменных для второго и четвертого параметров в этом предложении как раз и обеспечивает переприсваивание полученного значения. Все, что теперь остается сделать – это передать полученное значение факториала из рекурсивных вызовов, никак не изменяя его. Следует отметить применение отсечения в первом предложении для предиката factorial_aux. Отсечение в данном случае служит для того, чтобы убрать точку возврата, если цель Counter<=N успешно доказывается, соответственно второе предложение для предиката factorial_aux использовано заведомо не будет. Во втором предложении также нет проверки условия Counter>N, так как это излишне. Переход ко второму предложению будет выполнен, только если Counter будет больше, чем N. В качестве первого и третьего параметров используются анонимные переменные, так как в данном случае не важно ни значение переменной N, ни значение текущего счетчика Counter. Второе предложение можно переписать в более подробном варианте, factorial_aux (_, Factorial_N, _, Product):- Factorial_N=Product. однако так, как это предложение записано в примере выше, с точки зрения стиля программирования на Prolog’е, будет более грамотно. Дерево целей для случая вычисления факториала 3!. 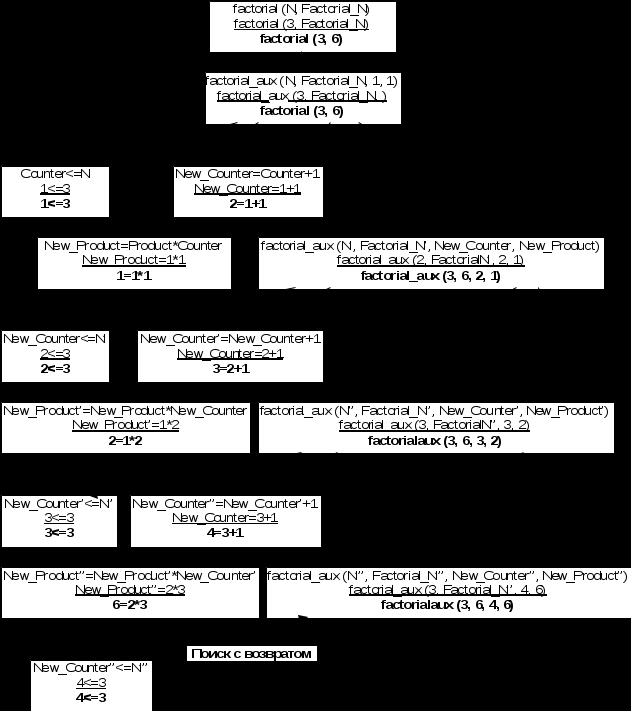 |
