цуим. Цифровые_устройства. Основы теории конечных автоматов, приобретение практических навыков рас
 Скачать 1.61 Mb.
|
|
3.Совершенная дизъюнктивная нормальная форма  Каждому члену СДНФ соответствует единичное значение функции. 4. Проведем склеивание и поглощение, получим сокращенную форму. Склеиваются следующие пары членов: 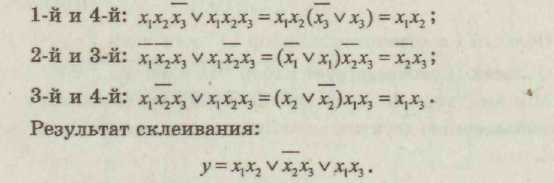 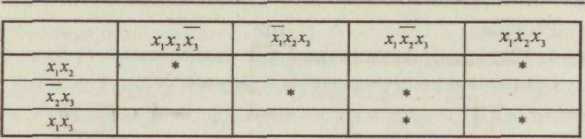 5. Сокращенная форма содержит лишний член. Для перехода к минимальной форме строим импликантную таблицу. Импликанты  составляют ядро, поэтому немогут быть исключены. Исключаем из сокращенной формы импликанту  6. Получаем минимальную дизъюнктивную форму  7. Для проверки полученного результата проведем минимизацию другим методом — с использованием карт Карно.  Минимальная дизъюнктивная форма представляет собой дизъюнкцию двух конъюнкций, соответствующих двум областям:  Минимальные ДНФ, полученные различными методами, совпадают. 8. Построим структурную схему устройства по полученной минимальной ДНФ (рис. 7). 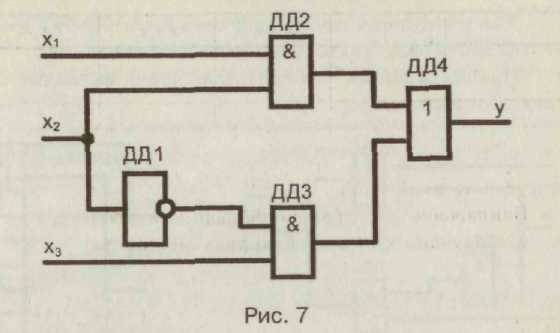 Структурная схема содержит всего 4 элемента вместо 6 в первоначальной схеме. Значительно сокращено число межэлементных соединений. Однако в схеме использованы 3 различных элемента НЕ (ДД1), И (ДД2, ДДЗ), ИЛИ (ДД4). 9. Синтезируем схему в базисе 2И-НЕ. 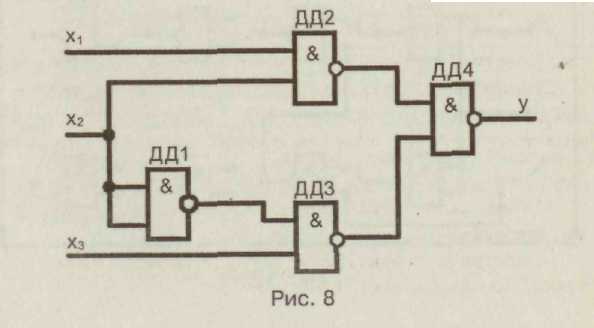  10. Построим структурную схему устройства в базисе 2И-НЕ. Для построения схемы из 4 элементов 2И-НЕ достаточно взять одну микросхему типа К555ЛАЗ. 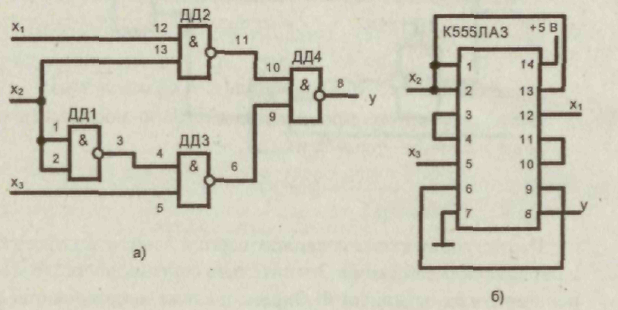 Принципиальная электрическая схема выглядит следующим образом (рис. 9) Рис. 9 11. По этой схеме собирается лабораторная установка для проведения экспериментальных исследований (рис. 10). 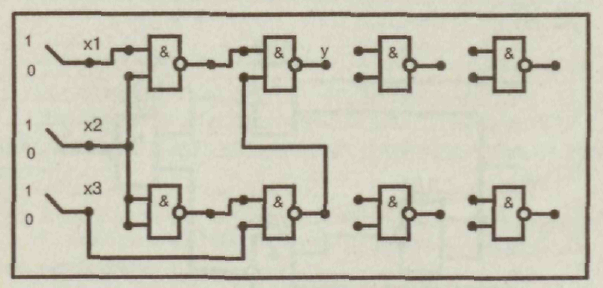 Рис. 10 На входы х1, х2, х3подаем стандартные сигналы 000, 001,010,011, 100, 101, 110, 111 и вольтметром на выходе V проверяем логические уровни на соответствие таблице истинности. 12. Для построения комбинационного автомата в базисе 2ИЛИ-НЕ составляем совершенную конъюнктивную нормальную форму  Каждому члену произведения СКНФ соответствует нулевое значение функции. 13. Проведем склеивание и поглощение, получим сокращенную форму. Склеиваются следующие пары членов: 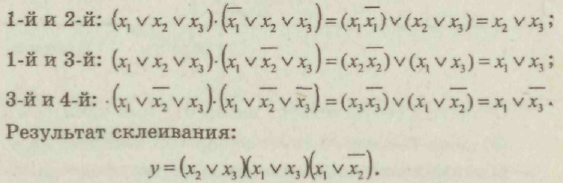 14. Для перехода к минимальной форме строим имп-ликантную таблицу. 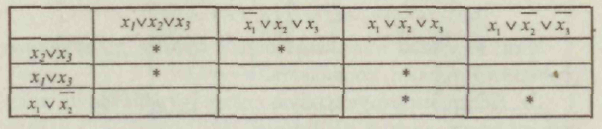 Импликанты х2 v х3, х1 v х2составляют ядро, поэтому не могут быть исключены. Исключаем из сокращенной формы импликанту х1 v х3. 14. Получаем минимальную конъюнктивную форму:  Прямой подстановкой значений переменных х1, х2 х3можно убедиться, что данная минимальная конъюнктивная форма соответствует таблице истинности. 15. Для проверки полученного результата проведем минимизацию также и другим методом — с использованием карт Карно. 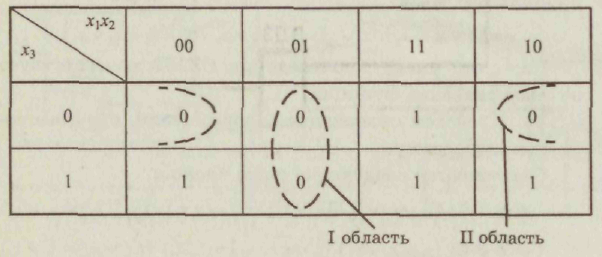 Области I соответствует набор 01* или член (х1 v х2) Области II соответствует набор *00 или член (х2 v х3). Минимальная конъюнктивная форма представляет собой конъюнкцию двух дизъюнкций, соответствующих двум областям:  Минимальные конъюнктивные формы, полученные разными методами, совпадают. 16. Построим структурную схему устройства по полу- ченной минимальной КНФ (рис. 11). Структурная схема содержит 4 элемента. Причем используются различные элементы: НЕ (ДД1), ИЛИ (ДД2, ДДЗ), И (ДД4). 17. Синтезируем схему в базисе ИЛИ-НЕ. Для этого используем формулы де Моргана. В результате преобразований получим 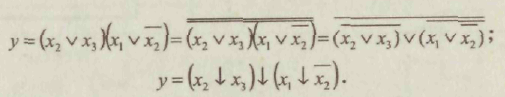 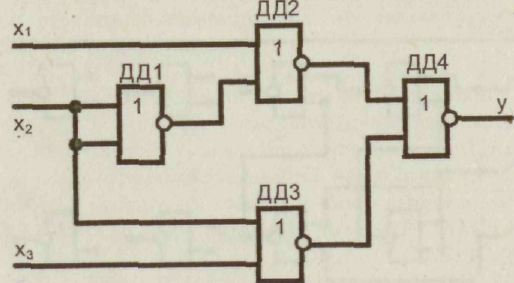 Рис. 12 Построим структурную схему устройства в базисе 2ИЛИ-НЕ (рис. 12). Для технической реализации схемы из 4 элементов 2ИЛИ-НЕ достаточно взять одну микросхему К 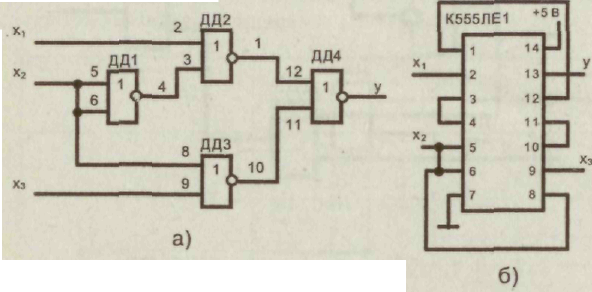 555ЛЕ1. Принципиальная электрическая схема выглядит следующим образом, (рис. 13).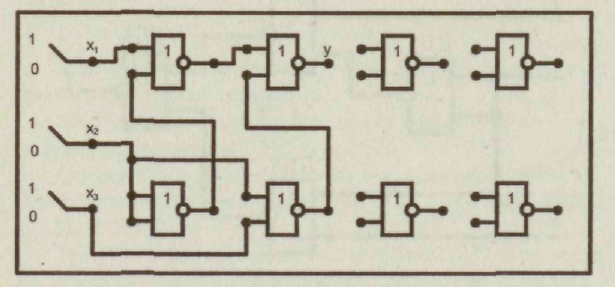 Рис. 13 На этой схеме наглядно видно, какие монтажные соединения необходимо выполнить на микросхеме К555ЛЕ1. 19. Собираем лабораторную установку для экспериментальной проверки результатов расчета (рис. 14). Рис. 14 На входы х1 х2х3 подаем стандартные сигналы 000, 001, 010, 011, 100, 101, 110, 111 и вольтметром на выходе у измеряем уровень напряжения. Проверяем соответствие таблице истинности. Исходная схема и варианты заданий 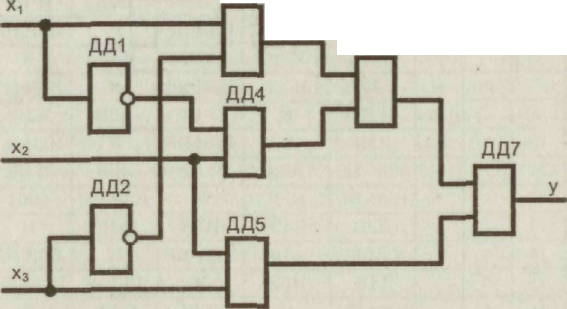 ДД1, ДД3 — инверторы, прочерк в таблице соответствует отсутствию инвертора, знак «*» соответствует наличию инвертора в схеме.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||