цуим. Цифровые_устройства. Основы теории конечных автоматов, приобретение практических навыков рас

• Название: Основы теории конечных автоматов, приобретение практических навыков рас
• Дата: 30.11.2021
• Размер: 1.61 Mb.
• Имя файла: Цифровые_устройства.docx
• Тип: Документы; #287063
• страница: 1 из 3

ДОМАШНЕЕ ЗАДАНИЕ

ПО ДИСЦИПЛИНЕ

«ЦИФРОВЫЕ УСТРОЙСТВА

И МИКРОПРОЦЕССОРЫ»

Введение

Главной целью домашнего задания является закрепле­ние теоретических знаний по теме «Основы теории конеч­ных автоматов», приобретение практических навыков рас­чета, анализа и синтеза простейших комбинационных схем на логических элементах и проведения эксперименталь­ных исследований по определению логических функций, устройств на интегральных микросхемах и устройств, по­строенных на ПЭВМ в системе Еlесtгоnics WоrkBеnсh.

На выполнение задания отводится 10 часов самостоя­тельной работы.

По окончании выполнения домашнего задания пред­ставляется пояснительная записка в сброшюрованном виде на листах формата 11 (297 х 210 мм). На титульном листе должны быть указаны наименование кафедры; наимено­вание дисциплины; заголовок домашнего задания; номер варианта, фамилия и инициалы студента; фамилия и ини­циалы преподавателя, дата и место выполнения.

В тексте пояснительной записки приводится содержа­ние задания, исходные данные и условия, вычерчиваются необходимые схемы. Все основные положения, приводимые в расчетах, должны сопровождаться обоснованием. При записи цифровых данных и результатов измерений необходимо указывать единицы измерений. Все записи, таблицы, схемы должны выполняться с соблюдением тре­бований ЕСКД. При выполнении экспериментальных ис­следований необходимо указывать используемое лабора­торное оборудование, макеты, измерительные приборы и их характеристики, К пояснительной записке приклады­ваются программы и результаты расчета на ПЭВМ, вы­черчиваются графики и осциллограммы. В конце поясни­тельной записки ставится личная подпись студента» вы­полнявшего домашнее задание.

Варианты задач домашнего задания для каждого обу­чаемого приведены в приложении и определяются поряд­ковым номером в журнале.

1. Содержание домашнего задания

Домашнее задание предполагает последовательное ре­шение следующих задач:

1. 
   По принципиальной электрической схеме провести анализ и установить функциональную зависимость в виде формул алгебры логики и таблицы истинности.
   
2. 
   По заданной таблице истинности составить совер­шенную дизъюнктивную нормальную форму (СДНФ) и совершенную конъюнктивную нормальную форму(СКНФ).
   

3. 
   Минимизировать логическую функцию любым из­ вестным методом.
   
4. 
   Синтезировать комбинационное устройство в задан­ном базисе И-НЕ, ИЛИ-НЕ.
   
5. 
   Синтезировать комбинационное устройство в заданном базисе двухвходовых элементов 2И-НЕ, 2ИЛИ-НЕ.
   
6. 
   Экспериментально проверить результаты расчета и работу синтезированного устройства на лабораторном ма­кете на микросхемах 555 серии.
   
7. 
   Экспериментально проверить работу синтезирован­ного устройства на ПЭВМ в системе Electronics Workbench.
   

2. Методические указания

по выполнению задания.

Основные теоретические

положения

Интегральные логические микросхемы имеют широ­кий набор различных логических элементов, функциональ­ных узлов цифровых устройств. Они отличаются высокой надежностью, малыми габаритами и массой, малым по­треблением энергии. Реальные цифровые комбинацион­ные устройства выполняются с использованием интеграль­ных микросхем.

Дискретный автомат — комбинационное устройство без памяти можно представить в виде п, т — многополюсни­ка (рис. 1).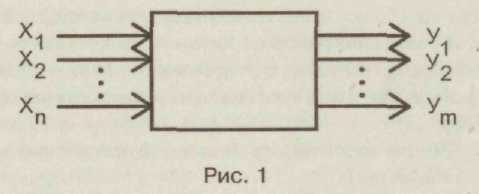



Условия функционирования дискретного автомата мож­но представить в виде системы логических функций, на­зываемых функциями выходов: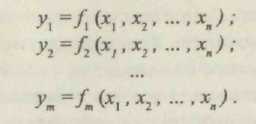



Задача анализа условия функционирования сводится к определению всех функций выхода автомата по извест­ной принципиальной электрической схеме реального уст­ройства. Результат анализа представляется в виде функ­ций алгебры логики и таблицы истинности. Другими сло­вами, необходимо установить функциональную зависи­мость между входными переменными дискретного авто­мата и значениями выходных дискретных сигналов в виде формул алгебры логики и таблицы истинности.

Анализ дискретного автомата целесообразно проводить в следующей последовательности:

l.Ha функциональной схеме дискретного автомата выходы всех логических элементов (ЛЭ) обозначить сим­волами промежуточных переменных.

2. 
   Определить и записать функции непосредственных связей, устанавливающие зависимости выхода каждого ЛЭ от его входов.
   
3. 
   Путем подстановок исключить все внутренние переменные. Получить зависимости выходов комбинационно­го устройства от его входов.
   
4. 
   Составить таблицу истинности.
   

После составления таблицы истинности целесообразно перейти к совершенной дизъюнктивной нормальной фор­ме (СДНФ) и к совершенной конъюнктивной нормальной форме (СКНФ).

Дизъюнктивной нормальной формой (ДНФ) называет­ся такая форма представления функции, при которой ло­гическое выражение строится в виде дизъюнкции (логи­ческой суммы) ряда членов, каждый из которых является простой конъюнкцией (логическим произведением) аргу­ментов или их инверсий. Каждый аргумент или его ин­версия в конъюнкцию входит один раз. Если в каждом члене ДНФ представлены все аргументы (или их инвер­сии) функции, то такая форма называется совершенной ДНФ (СДНФ).

Совершенная дизъюнктивная нормальная форма из таблицы истинности получается по следующему простому алгоритму. Она построена из суммы конъюнкций, кото­рые составлены в соответствии только с теми комбинаци­ями значений переменных, на которых функция прини­мает значение единицы. В конъюнкцию собираются в ка­честве сомножителей без знака отрицания все аргументы, значения которых в наборе равны 1, и со знаком отрица­ния (инверсии) те аргументы, значения которых в наборе равны 0. Число конъюнкций в совершенной дизъюнктив­ной нормальной форме равно числу единичных значений функции на всех возможных комбинациях значений ее аргументов (переменных). Так как члены СДНФ связаны операцией дизъюнкции, то при обращении в единицу од­ного из членов функция оказывается равной единице. Любая функция имеет единственную СДНФ.

Конъюнктивной нормальной формой (КНФ) называет­ся форма представления функции в виде конъюнкции (ло­гического произведения) ряда членов, каждый из кото­рых является простой дизъюнкцией аргументов или их инверсий. Каждый аргумент или его инверсия в дизъюнк­цию входит один раз. Если в каждом члене КНФ пред­ставлены все аргументы (или их инверсии), то такая фор­ма называется совершенной конъюнктивной нормальной формой (СКНФ).

Совершенная конъюнктивная нормальная форма из таблицы истинности получается по следующему простому алгоритму. Она построена из логического произведения дизъюнкций, которые составлены в соответствии только с теми комбинациями значений переменных, на которых функция принимает нулевое значение. В дизъюнкцию собираются в качестве слагаемых без знака отрицания все аргументы, значения которых в наборе равны 0, и со зна­ком отрицания (инверсии) те аргументы, значения кото­рых в наборе равны 1.

Выражение для СКНФ содержит столько членов, сколь­ко нулей имеется среди значений функции в таблице ис­тинности. Таким образом, каждому набору значений ар­гументов, на коте ром функция равна нулю, соответствует определенный член СКНФ, принимающий на этом наборе значений нуль. Так как члены СКНФ связаны операцией конъюнкции, то при обращении в нуль одного из членов функция оказывается равной нулю. Любая функция име­ет единственную СКНФ.

Структурная схема логического устройства может быть построена непосредственно по канонической форме (СДНФ или СКНФ) реализуемой функции. Но получающиеся схе­мы чаще всего неоправданно сложные, требуют использо­вания большого числа логических элементов, имеют низ­кие экономичность и надежность. Представление функ­ции в виде СДНФ или СКНФ может быть сокращено. Методы упрощения функции называются методами ми­нимизации функций.

Для минимизации алгебраических выражений исполь­зуются известные соотношения булевой алгебры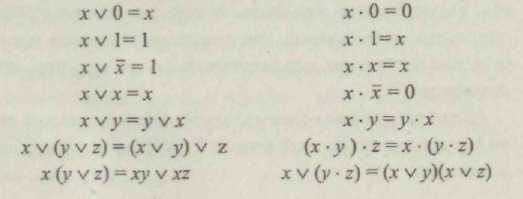









Из этих основных соотношений следуют, например, та кие полезные соотношения, как










из дискретного анализа известно, что существуют та­кие формулы представления функции, которые дальше уже нельзя упростить. Они называются сокращенными. Известно также, что не всякая сокращенная форма явля­ется минимальной. Однако минимальную по числу пере­менных следует искать среди сокращенных форм. Пере­ход к сокращенной форме основан на последовательном применении двух операций: операции склеивания и опе­рации поглощения.

Для выполнения операции склеивания в выражении функции выявляются пары членов вида


различающиеся лишь тем, что один из аргументов в одном из членов представлен без инверсии, а в другом — с инверсией. Затем проводится склеивание таких пар членов:

Член wпоглощает член н> г. При проведении этой опе­рации из логического выражения вычеркиваются все чле­ны, поглощаемые членами, которые введены в результате операции склеивания. Операции склеивания и поглоще­ния выполняются последовательно до тех пор, пока это возможно.







Результаты склеивания wвводятся в выражение функции. Операция поглощения основана на равенстве

• 
  исходной формой для минимизации логического
  выражения является СКНФ;
  
• 
  пары склеиваемых членов имеют вид
  

Для получения минимальной конъюнктивной нормаль­ной формы логической функции имеются следующие осо­бенности:





• операция поглощения проводится в соответствии с выражением

Сокращенная форма может содержать лишние члены, исключение которых из выражения не повлияет на значе­ние функции. Дальнейшее упрощение логического выра­жения достигается исключением из выражения лишних членов. В этом заключается содержание минимизации.

Целью минимизации логической функции является уменьшение стоимости ее технической реализации. Кри­терий минимизации далеко не однозначен и зависит как от типа решаемой задачи, так и от технологии. С развити­ем микроэлектроники критерии минимизации претерпе­ли существенные изменения. Стоимость БИС и СБИС оп­ределяется в основном площадью схемы на кристалле и мало зависит от числа входящих в нее транзисторов и других элементов. На первое место при проектировании самих ИС выдвигается требование регулярности внутрен­ней структуры и минимизации числа внешних соедине­ний даже за счет увеличения числа элементов и внутрен­них соединений. Эти требования диктуются требования­ми повышения надежности электронных средств.

Однако при проектировании аппаратуры с применени­ем БИС и СБИС, требование уменьшения числа корпусов ИС и их межсоединений по-прежнему остается важным.

Минимизацию логической функции можно проводить любым известным методом, например, методами Квайна — Мак-Класки, методом Петрика, с использованием карт Вейча, карт Карно. Методы минимизации изучаются в теоретическом курсе.

В результате минимизации получается логическая функция, для технической реализации которой необходи­мо использовать разнообразные логические элементы: И, ИЛИ, НЕ. В то. же время с точки зрения обеспечения ре­гулярной структуры устройство требуется строить на од­нотипных элементах.

Программируемые логические СБИС и полузаказные СБИС на основе базовых матричных кристаллах содержат отдельные нескоммутированные между собой элементар­ные логические элементы 2И-НЕ либо 2ИЛИ-НЕ, кото­рые могут быть соединены между собой в соответствии с заданным алгоритмом обработки логических сигналов.

Для синтеза функции в базисе ИЛИ-НЕ получают нор­мальную минимальную конъюнктивную форму, дважды ее инвертируют, далее проводят преобразование по фор­муле де Моргана.




При синтезе в базисе И-НЕ должна быть получена минимальная нормальная дизъюнктивная форма. Преоб­разование проводят по другой формуле де Моргана в виде


Обычно задается не только тип логического элемента, но и число его входов. При этом реальное число входов заданных логических элементов не соответствует числу переменных в полученных после соответствующего преоб­разования выражениях. Рассмотрим ситуацию, когда число входов логического элемента меньше числа переменных, входящих в реализуемую с их помощью функцию алгеб ры логики. На рис. 2 показан способ реализации трехбук­венного члена логического выражения функции на раз­личных типах элементов с двумя входами 2ИЛИ-НЕ (рис. 2, а), 2И-НЕ (рис. 2, б).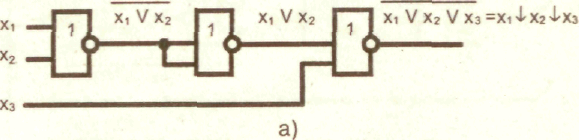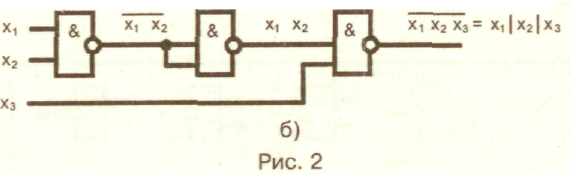





Для технической реализации логической функции в этих случаях следует провести соответствующее преобразование групп членов на основе тождественных соотношений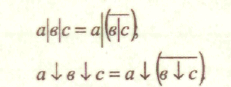



Для экспериментальной проверки результатов расчета необходимо собрать схему на лабораторных макетах и, по­давая на входы варианты комбинаций, входных сигналов х_г х_г, х , определить значения выходной переменной. Схема лабораторного макета для синтеза схемы в ба­зисе ИЛИ-НЕ показана на рис. 3, а. Она построена на микросхемах К555ЛЕ1. Лабораторный макет для синтеза комбинационных устройств в базисе 2И-НЕ (рис. 3, б) вы­полнен на микросхемах К555ЛАЗ.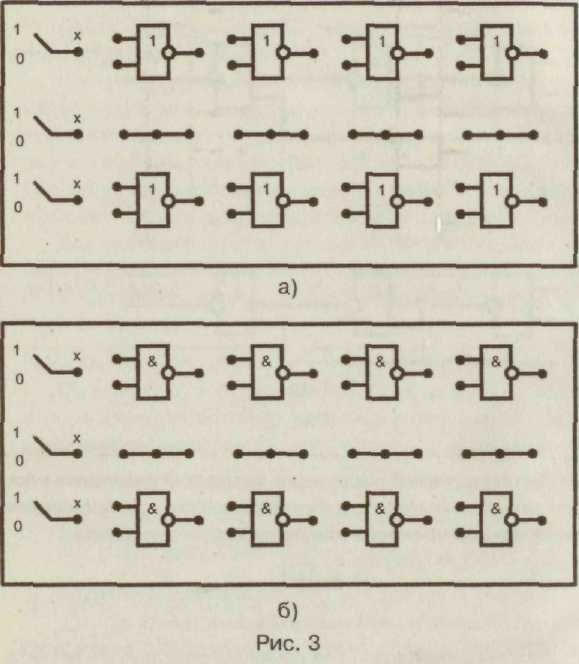


Условное графическое обозначение микросхем К555ЛАЗ и К555ЛЕ1 приведены на рис. 4. а, б.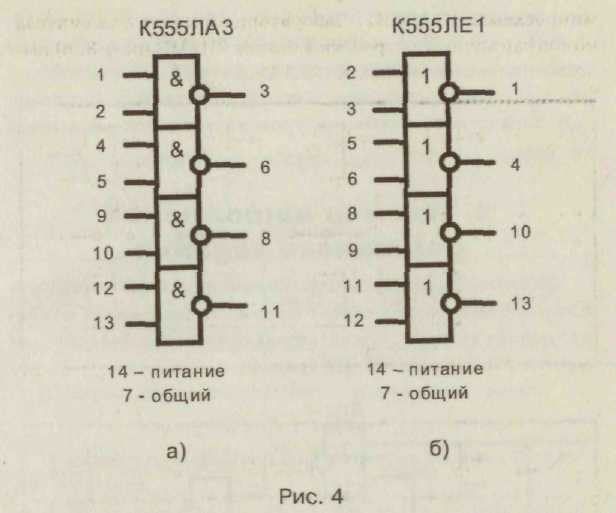




Питание микросхем 555 серии — стандартное для мик­росхем ТТЛ, ТТЛШ и составляет 5В.
Моделирование работы устройства на ЭВМ в системе Electronics Workbench можно проводить на всех этапах расчета и выполнения домашнего задания. Для сборки не­обходимо использовать элементы НЕ, И, ИЛИ, И-НЕ, ИЛИ-НЕ (рис. 5).





К входам схем подключить генератор слов, и к выходу логический пробник. Генератор слов запрограммирован на формирование последовательности из восьми слов, соот ветствующих числам от 0 до 7: 0 = 000; 1 = 001; 2 = 010; 3 = 011; 4 = 100; 5 = 101; 6 = ПО; 7 = 111. В пошаговом режиме, последовательно подавая на вход полученной схе­мы все слова последовательности, определить при помо­щи логического пробника уровень сигналов на выходе схемы.