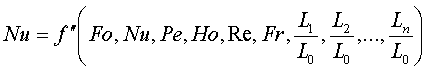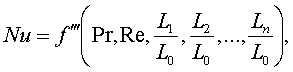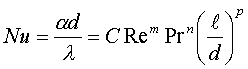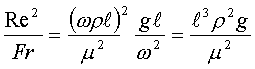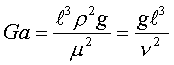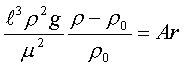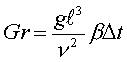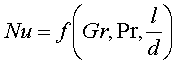Основы теплопередачи (краткие сведения с формулами). Основы теплопередачи
 Скачать 215.5 Kb. Скачать 215.5 Kb.
|
1=const и, значит, критерий Pr можно исключить из обобщённых уравнений для определения ОСНОВЫ ТЕПЛОПЕРЕДАЧИ Перенос энергии в форме тепла, происходящий между телами, имеющими различную температуру, называется теплообменом. Тела, участвующие в теплообмене, называются теплоносителями. Теплопередача – процесс распространения тепла. Способы переноса тепла: теплопроводность (реализуется внутри твёрдых тел), конвекция (возникает в результате перемешивания в жидкостях и газах), тепловое излучение (лучеиспускание). В реальных условиях тепло передаётся комбинированным способом. Например, при теплообмене между твёрдой стенкой и газовой средой тепло передаётся одновременно конвекцией, теплопроводностью и излучением (теплоотдача). Ещё более сложным является процесс передачи тепла от более нагретой жидкости (газа) через разделяющую их поверхность (теплопередача). Расчёт теплообменной аппаратуры включает: Определение теплового потока путём составления и решения тепловых балансов. Определение поверхности теплообмена из основного уравнения теплопередачи. Тепловой баланс Количество теплоты (Дж/с), которое отдаёт горячий теплоноситель, Аналогично количество теплоты (Дж/с), которое получит холодный теплоноситель, где G – массовый расход горячего (холодного) теплоносителя, кг/с, c - удельная теплоёмкость теплоносителя, Дж/(кгК), tн - начальная температураи tк – конечная температура теплоносителя. Из-за потерь теплоты в окружающую среду через наружные стенки аппарата холодный теплоноситель получит не всю теплоту, отданную горячим теплоносителем, т.е. Уравнение теплового баланса Уравнение справедливо, если теплоносители не изменяют агрегатного состояния. Если в качестве горячего теплоносителя используют насыщенный водяной пар, то количество теплоты, выделяющейся при конденсации пара, где D – массовый расход пара, кг/с, r – скрытаятеплота парообразования, Дж/кг, тогда Если в аппарате охлаждается образовавшийся конденсат, необходимо учесть теплоту, выделяемую конденсатом: где cкон – удельная теплоёмкость конденсата, Дж/(кгК), tп – температура греющего пара, равная температуре конденсации, 0С, tкон – температура конденсата, покидающего аппарат, 0С. В современных тепловых аппаратах тепловые потери благодаря тепловой изоляции не превышают 3…5% количества теплоты, выделяемой горячим теплоносителем, и в приближённых расчётах могут не учитываться. Конвекция включает в себя два механизма переноса тепла – за счёт теплопроводности и за счёт перемешивания, а их вклад в процесс зависит от гидродинамических характеристик движения жидкости или газа. Основное уравнение теплоотдачи Количество теплоты, передаваемой от горячего теплоносителя, прямо пропорционально площади теплопередающей поверхности F, действующей средней разности температур Δt, продолжительности процесса τ и коэффициенту теплоотдачи Коэффициент теплоотдачи 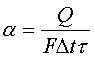 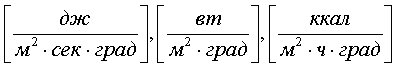 Коэффициент теплоотдачи зависит от: - скорости жидкости - тепловых свойств жидкости (удельной теплоёмкости ср, теплопроводности - геометрических параметров – формы и определяющих размеров стенки (для труб – их диаметр d и длина L), а также шероховатости Вследствие сложной зависимости коэффициента теплоотдачи Для определения коэффициента теплоотдачи 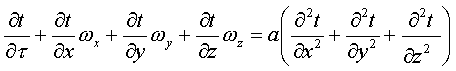 где 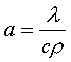 , , 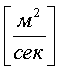 где с – теплоёмкость, Дифференциальное уравнение конвективного теплообмена или уравнение Фурье-Кирхгофа: 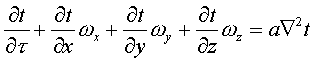 Коэффициент температуропроводности Для твёрдых тел Следовательно, 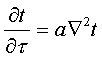 При установившемся процессе теплообмена 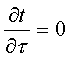 Для практического использования уравнения Фурье-Кирхгофа его представляют в виде функции от критерия подобия. 1. Подобие граничных условий (подобие процессов теплопереноса на границе между стенкой и потоком жидкости) характеризуется критерием Нуссельта: 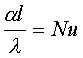 Nu является мерой соотношения толщины пограничного слоя 2. Условие подобия в ядре потока выражает критерий Фурье (равенство критериев Фурье в сходственных точках тепловых потоков - необходимое условие подобия неустановившихся процессов теплообмена): 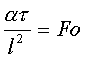 3. Критерий Фурье является аналогом критерия гомохронности Ho при гидродинамическом подобии (учитывает неустановившийся характер движения в подобных потоках). 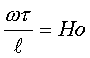 4. Критерий Пекле является мерой соотношения между теплом, переносимым путём конвекции и путём конвекции и путём теплопроводности при конвективном теплообмене: 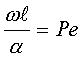 5. Критерий Рейнольдса отражает влияние силы трения на движение жидкости (характеризует отношение инерционных сил к силам трения в подобных потоках): 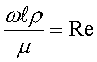 6. Критерий Фруда отражает влияние силы тяжести, или собственного веса, на движение жидкости (является мерой отношения силы инерции к силе тяжести в подобных потоках): 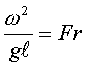 Необходимыми условиями подобия процессов переноса тепла является соблюдение гидродинамического (характеризуется равенством критериев Ho, Re, Fr в сходственных точках подобных потоков)и геометрического подобия (характеризуется постоянством отношения основных геометрических размеров стенки L1, L2, …Ln к некоторому характерному размеру L0 = d – обычно диаметру трубы). Таким образом, обобщённое (критериальное) уравнение конвективного теплообмена выражается функцией вида: 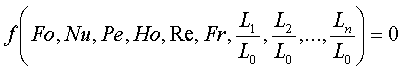 или с учётом того, что критерий Нуссельта является определяемым, так как в него входит искомая величина коэффициента теплоотдачи: 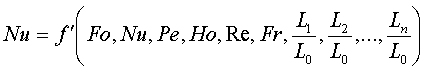 7. 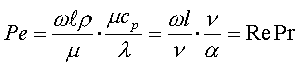 где 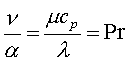 - критерий Прандтля (характеризует подобие физических свойств теплоносителей в процессах конвективного теплообмена) является мерой подобия полей температур и скоростей). - критерий Прандтля (характеризует подобие физических свойств теплоносителей в процессах конвективного теплообмена) является мерой подобия полей температур и скоростей). Значения критерия Прандтля для капельных жидкостей порядка 3 – 300 и значительно уменьшаются с возрастанием температуры, а для газов постоянны и зависят от атомности газа (Pr | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тип задачи (движение жидкости) | Вид функции | Критериальное уравнение | Развёрнутое критериальное уравнение | Область применения | |||||||||||||
| Внутри труб | Nu =(Re,Pr) | Nu=0.023Re0.8 Pr0.4 | 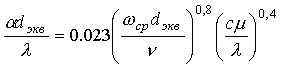 (*) (*) | Развитое турбулентноедвижение Re>104 | |||||||||||||
| Nu=0.008Re0.9 Pr0.43 | Переходный режим 2300 | ||||||||||||||||
| Nu=0.17Re0.33Pr0.43Gr0.1 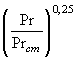 | Ламинарный режим | ||||||||||||||||
| В аппаратах с мешалкой | Nu =(Re,Pr) | Nu=СReм mPrж n 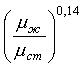 (**) (**)Значение коэффициента C и показателей степеней m и n
| | ||||||||||||||
| В аппаратах с естественной конвекцией | Nu =(Gr,Pr) | Nu =С(GrPr)n | С | n | Ламинарный GrPr<500 | ||||||||||||
| 1.18 | 0.125 | ||||||||||||||||
| 0,54 | 0,25 | Переходный GrPr=500 - 2х107 | |||||||||||||||
| 0,135 | 0,33 | Турбулентный GrPr>2х107 | |||||||||||||||
(*) – эквивалентный диаметр, S – площадь поперечного сечения потока, П – смоченный периметр сечения (для труб круглого сечения dэкв равен внутреннему диаметру трубы),
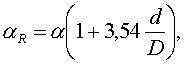
где d – внутренний диаметр трубы змеевика, D – диаметр витка змеевика.
(**)
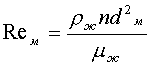 - критерий Рейнольдса, модифицированный для мешалок, dм - диаметр мешалки, n - число оборотов мешалки в 1 сек,
- критерий Рейнольдса, модифицированный для мешалок, dм - диаметр мешалки, n - число оборотов мешалки в 1 сек, Теплоотдача при изменении агрегатного состояния
Конденсация паров
Сухой насыщенный пар, поступающий в аппарат в качестве горячего теплоносителя, конденсируется на теплопередающей поверхности, выделяя большое количество теплоты. При этом образующаяся жидкая фаза – конденсат – выделяется на поверхности в виде отдельных капель. Происходит капельная конденсация. В реальных аппаратах поверхность теплоотдачи ограничена, а количество пара, поступающего на конденсацию, велико. Это приводит к быстрому слиянию капель и образованию плёнки, покрывающей всю теплопередающую поверхность. Общее критериальное уравнение для этого случая теплоотдачи имеет вид:
где Ku – критерий Кутателадзе – критерий фазового перехода, который служит мерой отношения теплоты, затрачиваемой на фазовое превращение, к теплоте переохлаждения (перегрева) жидкой фазы при температуре её насыщения:
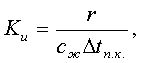
где r – скрытая теплота парообразования (теплота конденсации), Дж/кг, сж - удельная теплоёмкость конденсата, Дж/(кг. К),
так как
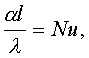
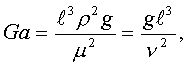
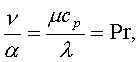
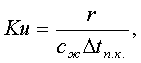
то
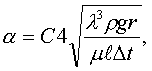
где
C – коэффициент, зависящий от формы поверхности.
Для вертикальных плоских и трубчатых поверхностей C = 2.04, l= H (высота вертикальной стенки трубы), тогда
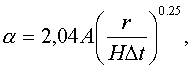
где
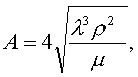 для горизонтальной поверхности С =1,28, l = dн (наружный диаметр трубы), тогда
для горизонтальной поверхности С =1,28, l = dн (наружный диаметр трубы), тогда 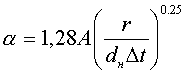
Ориентировочные интервалы значений коэффициентов теплоотдачи в промышленных теплообменных устройствах
| | Вт / (м2град) | Ккал / (м2ч град) |
| При нагревании и охлаждении - воздуха - перегретого пара - масел - воды | 1,16 – 58 23,2 – 116 58 – 1 740 232 – 11 600 | 1,0 – 50 20 – 100 50 – 1 500 200 – 10 000 |
| При кипении воды | 580 – 52 200 | 500 – 45 000 |
| При плёночной конденсации водяных паров | 4 640 – 17 400 | 4 000 – 15 000 |
| При конденсации паров органических веществ | 580 – 2 320 | 500 – 2 000 |
Уравнение теплопередачи для плоской стенки при постоянных температурах теплоносителей
и для непрерывных процессов
Коэффициент теплопередачи
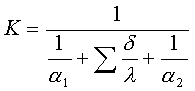
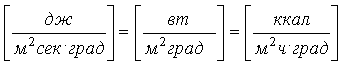
Коэффициент теплопередачи K показывает, какое количество тепла переходит в единицу времени от более нагретого к менее нагретому теплоносителю через разделяющую их стенку поверхностью 1 м2 при разности температур между теплоносителями 1 град.
Уравнение теплопередачи для цилиндрической стенки при постоянных температурах теплоносителей
где
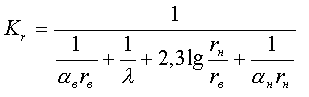
линейный коэффициент теплопередачи, отнесённый к единице длины трубы, а не к единицы её поверхности, т.е.
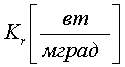 ,
,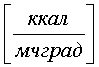 .
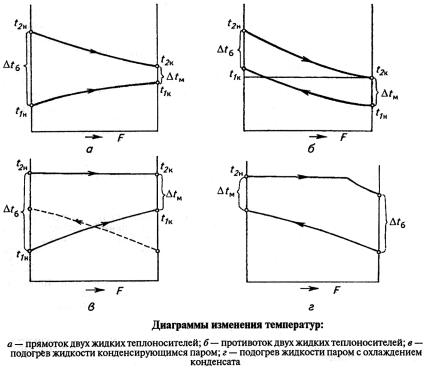
. Расчет средней разности температур при различных направлениях движения теплоносителей
Перемещаясь вдоль поверхности теплообмена, теплоносители непрерывно изменяют свою температуру.
Диаграммы изменения температур
Если разность температур на входе в аппарат превышает разность на выходе не более чем в два раза, т.е.
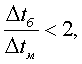 среднюю разность определяют как среднюю арифметическую:
среднюю разность определяют как среднюю арифметическую: 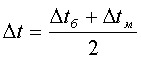
Если разности температур отличаются более чем в два раза, т.е.
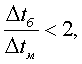 среднюю разность определяют как среднюю логарифмическую:
среднюю разность определяют как среднюю логарифмическую: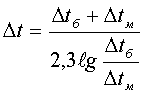
В случае, когда теплоносители движутся навстречу один другому в противотоке (рис. б), действующая разность температур в каждом сечении аппарата гораздо ближе к средней разности
Теплообменниками называют аппараты, предназначенные для передачи тепла от одних веществ к другим.
Вещества, участвующие в процессе передачи тепла, называются теплоносителями. Теплоносители, имеющие более высокую температуру, чем нагреваемая среда, и отдающие тепло, называют нагревающими агентами, а теплоносители с более низкой температурой, чем среда, от которой они воспринимают тепло, - охлаждающими агентами. Вещества, получающие тепло от источников и отдающие его через стенку теплообменника нагреваемой среде, называют промежуточными теплоносителями.