ОВ. ОПТИЧЕСКОЕ ВОЛОКНО_ЧАСТЬ 2. Основные характеристики потерь и искажений сигналов в оптическом волокне (Часть 2)
 Скачать 280.24 Kb. Скачать 280.24 Kb.
|
|
Основные характеристики потерь и искажений сигналов в оптическом волокне (Часть 2) Волокно характеризуется двумя важнейшими параметрами: затуханием и дисперсией. Чем меньше затухание (потери) и чем меньше дисперсия распространяемого в волокне сигнала, тем больше может быть длина линии связи. 1. Затухание в оптическом волокне Затухание в оптическом волокне - это мера ослабления оптической мощности, распространяемой вдоль ОВ между двумя его поперечными сечениями на данной длине волны. Затухание в ОВ выражается в дБ. Коэффициент затухания в OB - это величина затухания на единице длины волокна и выражается в дБ/км. Коэффициент затухания в ОВ обуславливается следующими факторами: потери за счет Рэлеевского рассеяния; потери за счет поглощения в инфракрасной и ультрафиолетовой областях частотного диапазона; кабельные потери; потери на макро- и микроизгибах. 1.1. Собственные потери Затухание с одной стороны, обусловлено наличием в оптическом волокне неоднородностей, расстояние между которыми меньше длины волны, а с другой - тепловыми флуктуациями показателя преломления. Свет, попадая на неоднородности, рассеивается в разных направлениях. В результате часть его теряется в оболочке. Составляющую коэффициента затухания ОВ, вызванную Рэлеевским рассеянием, можно определить из выражения 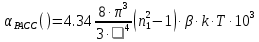 где: n1- ПП сердцевины и равен 1,48 -1,50; k= 1,38-10-23 Дж/К - постоянная Больцмана; Т = 1500 К - температура затвердевания стекла при вытяжке; β= 8,1∙10-11 м2 /Н - коэффициент сжимаемости стекла (для кварца). Введя постоянный коэффициент: 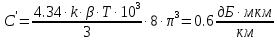 получим итоговую формулу для расчета затухания в ОВ, вызванного Рэлеевским рассеянием: 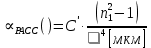 Потери за счет поглощения в ультрафиолетовой области частотного диапазона [дБ/км] определяются по формуле: 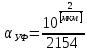 Потери в инфракрасной области спектра: 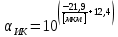 Полное затухание в волокне, измеряемое в дБ/км, определяется в виде суммы собственных и кабельных потерь: 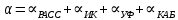 (2,17) (2,17)Величина кабельных потерь 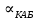 составляет 0,15-0,2 от собственных потерь. Они обусловлены скруткой, деформациями и изгибами волокон, возникающих при наложении покрытий и защитных оболочек при производстве кабеля, а также в процессе его прокладки. составляет 0,15-0,2 от собственных потерь. Они обусловлены скруткой, деформациями и изгибами волокон, возникающих при наложении покрытий и защитных оболочек при производстве кабеля, а также в процессе его прокладки.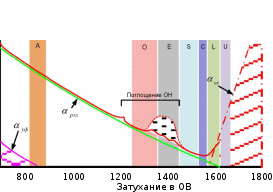 1.2. Потери на макро- и микроизгибах В ОВ кроме затухания, обусловленного потерями на рассеяние и поглощение в материале сердцевины, существуют потери, вызванные отклонениями структуры ОВ от оптимальной. И главной причиной этих потерь являются искривления оси ОВ и границы раздела сердцевина-оболочка. Различают макроизгибы, обусловленные конструкторско-технологическими или эксплуатационными факторами и случайные, хаотически расположенные по длине ОВ, - микроизгибы. Микроизгибы представляют собой мелкие локальные нарушения прямолинейности волокна, характеризуемые смещениями его оси в поперечных направлениях на участке микроизгиба. Основными причинами появления микроизгибов являются локальные поперечные механические усилия различного происхождения, приложенные к очень малым участкам волокна и появляющимися в процессе вытяжки волокна, перемотки и его хранения. Потери на микроизгибах: 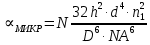 где h- высота микроизгиба, [мкм]; h≈(0,01÷0,1)d; N- число микроизгибов на 1 км ОВ; d- диаметр сердцевины, [мкм]; D- диаметр ОВ, [мкм]. 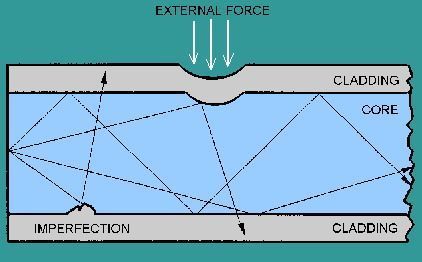 Потери на макроизгибах: Потери на макроизгибах: 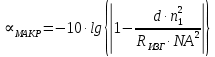 где RИЗГ- радиус изгиба (рассчитывается при R=1,2,5,10 см)  2. ДИСПЕРСИЯ ОПТИЧЕСКОГО ВОЛОКНА. ПОЛОСА ПРОПУСКАНИЯ ОВ 2.1 . Полоса пропускания и дисперсия в ОВ Рабочая полоса частот (полоса пропускания) ОВ определяет число передаваемых по нему каналов связи и зависит от дисперсии ОВ. Полоса пропускания МОВ обратно пропорциональна величине уширения импульсов. Если импульсы на входе и выходе ОВ имеют гауссовскую форму, то полоса пропускания определяется по формуле: 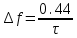 , ,где 𝜏- уширение импульсов на уровне 0,5 их амплитуды. Коэффициент широкополосности есть полоса пропускания ОВ, выраженная в МГц∙км, т.е: 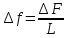 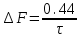 где 𝜏 - дисперсия на единицу длины. Дисперсия - уширение импульсов - определяется как квадратичная разность длительностей импульсов на выходе и входе кабеля длины L по формуле: 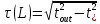 где tin- длительность импульса на входе кабеля; tout- длительность импульса н выходе кабеля; Обычно дисперсия нормируется в расчёте на 1 км, и измеряется в пс/км. Виды дисперсии представлены на рис. 2.6. 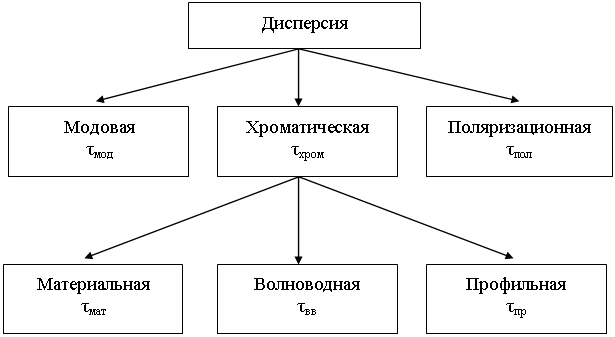 Чем меньше значение дисперсии, тем больший поток информации можно передать по волокну при заданной длине. Результирующая дисперсия г определяется из выражения: 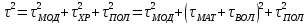 где: τМОД- межмодовая дисперсия; 𝜏ХР- хроматическая дисперсия, которая состоит из материальной 𝜏МАТ и волноводной 𝜏ВВ составляющих; 𝜏ПМД - поляризационно-модовая дисперсия. 2.2. Межмодовая дисперсия Межмодовая дисперсия возникает вследствие различной скорости распространения мод в МОВ и зависит от длины линии передачи. Для СППП: 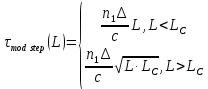 Для ГППП: 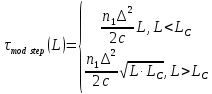 где LC-длина межмодовой связи (для ступенчатого волокна порядка 5-7 км, для градиентного - порядка 10-11 км). Как видно из уравнений, дисперсия для коротких линий (L < LC) увеличивается по закону L, а для длинных линий (L>LC) - по закону 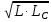 Для оптимального ППП: 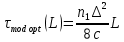 , , В настоящее время, коэффициент широкополосности градиентных ОВ составляет 500-600 МГц∙км на длине волны 0,85 мкм и 600-1200 МГц∙км на длине волны 1,3мкм. 2.3. Хроматическая дисперсия ООВ Хроматическая дисперсия ООВ состоит из материальной и волноводной составляющих и имеет место при распространении, как в одномодовом, так и в многомодовом волокне. Однако ее величина в МОВ крайне мала по сравнению с межмодовой дисперсией. Материальная дисперсия обусловлена зависимостью показателя преломления от длины волны, причём эта зависимость для одномодового волокна является дифференциальной. Уширение импульсов за счет материальной дисперсии на 1 км (пс/км): 𝜏мат()=∆∙M(), где ∆- ширина спектральной линии источника излучения (нм), M()-коэффициент удельной материальной дисперсии (пс/(нм∙км)). M()= 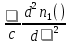 Для определения 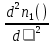 необходимо воспользоваться формулой Селмейера и вычислить ее в MathCad. Эмпирическая формула для расчета M(): необходимо воспользоваться формулой Селмейера и вычислить ее в MathCad. Эмпирическая формула для расчета M():M()= 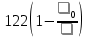 Формула справедлива для 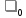 = 1,270 ÷1,290 мкми может быть использована только для оценки результатов расчета по предыдущей формуле. = 1,270 ÷1,290 мкми может быть использована только для оценки результатов расчета по предыдущей формуле.2.4. Волноводная дисперсия Волноводная дисперсия обусловлена зависимостью коэффициента распространения моды от длины волны. Уширение импульсов за счет волноводной дисперсии на 1 км (пс/км): 𝜏 ВОЛН() = ∆∙В() где В()-удельная волноводная дисперсия (пс/(нм∙км)). В()= 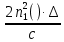 Результирующее значение коэффициента удельной хроматической дисперсии (пс/(нм∙км)) определяется как: D()=M()+В(). В зависимости от длины волны значение M()меняет знак. Значение В()всегда положительно. Длина волны, на которой D()=0 называется длиной волны нулевой дисперсии. Важным с практической точки зрения по ОВ всех типов является наклон кривой удельной хроматической дисперсии S0. 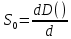 При заданной 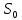 и 0 коэффициент удельной хроматической дисперсии для окон прозрачности (=1,280 ÷ 1,620 мкм) можно определить по формуле: и 0 коэффициент удельной хроматической дисперсии для окон прозрачности (=1,280 ÷ 1,620 мкм) можно определить по формуле: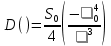 , , где 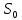 - наклон в точке нулевой дисперсии, - наклон в точке нулевой дисперсии,  - рабочая длина волны, - рабочая длина волны, 0 - длина волны нулевой дисперсии. Формула справедлива только для SMF - волокон. Для ОВ со смещенной дисперсией DSF (G.653) 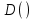 определяется по формуле: определяется по формуле: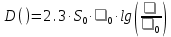 Уширение импульсов за счет хроматической дисперсии на 1 км (пс/км) определяется по формуле: 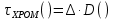 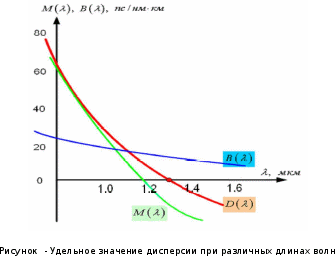 2.5. Поляризационная модовая дисперсия Поляризационная модовая дисперсия 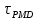 - возникает вследствие различной скорости распространения двух взаимно перпендикулярных поляризационных составляющих основной моды НЕ11 ООВ и наблюдается при В>2.5 Гбит/с и малых значениях ал . - возникает вследствие различной скорости распространения двух взаимно перпендикулярных поляризационных составляющих основной моды НЕ11 ООВ и наблюдается при В>2.5 Гбит/с и малых значениях ал .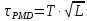 где Т- коэффициент удельной дисперсии 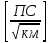 (типичное значение для кварцевого волокна Т = 0.08 ÷ 0.2 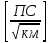 ) )Результирующая дисперсия ООВ:  . .3. КОМПЕНСАЦИЯ ДИСПЕРСИИ 3.1. Общие положения Для компенсации дисперсии в одномодовых волокнах используют специальный тип ОВ- DC волокно(DCF - DispersionCompensatingFiber-волокно для компенсации дисперсии). Профиль показателя преломления в DC волокнах выполнен в виде узкого центрального пика, окруженного кольцом с меньшим скачком показателя преломления:  На коротких длинах волн мода ведется в основном центральным пиком. С увеличением длины волны диаметр моды увеличивается, а модовый показатель преломления, соответственно, уменьшается. При этом изменяется коэффициент дисперсии волокна, величина которого пропорциональна (со знаком минус) второй производной по длине волны от эффективного показателя преломления волокна. Эта производная проходит через максимум, когда поле моды достигает кольца, окружающего центральный пик. Таким способом удается создавать волокна, обладающие большим (по модулю) отрицательным коэффициентом дисперсии. Обычно DC волокно наматывается на катушку, образуя модуль - модуль компенсации дисперсии (DCM - DispersionCompensationModule),который включается в определенных точках магистрали, так что среднее значение дисперсии ЭКУ (элементарного кабельного участка) 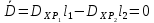 Возможности компенсации дисперсии волокон могут быть оценены с помощью коэффициента относительной крутизны дисперсионной кривой RDS, который определяется как отношение крутизны дисперсионной кривой к величине хроматической дисперсии : RDS = S/D, где Dи Sесть величина дисперсии и крутизна дисперсионной кривой на единицу длины соответственно. Если RDSволокна DSCF(DispersionanditsSlopeCompensationFiber - волокно со специально подобранной величиной дисперсии и наклона коэффициента дисперсии)является таким же, как и передающего волокна, то становится возможной полная компенсация наклона дисперсионной кривой передающего волокна путем подбора длины DSCF, подобно тому, как осуществляется компенсация полной дисперсии волокна. Степень компенсации наклона (Скн) может быть представлена следующим выражением : CКН=RDSDSCF/ RDSIF Если RDS волокна DSCF компенсатора и волокна одинаковы, то степень компенсации наклона составляет 100% и результирующая дисперсия после компенсации становится близкой к нулевому значению. Другой важной характеристикой DSCFкомпенсаторов является показатель качества, или эффективность (FOM). Он определяется как величина дисперсии на единицу потерь в волокне : FOM = Ddscf/𝜶dscf Примеры решения задач к разделу 1 «Затухание в оптическом волокне» 1. Рассчитать коэффициент затухания в ООВ для центральной длины волны стандартного диапазона при ПП сердцевины n1 = 1,46. Потери в кабеле не учитывать. Решение Центральная длина волны С диапазона = 1550нм, тогда потери на Релеевское рассеяние: 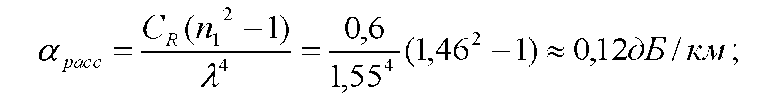 потери за счет поглощения в УФ и ИК диапазонах: 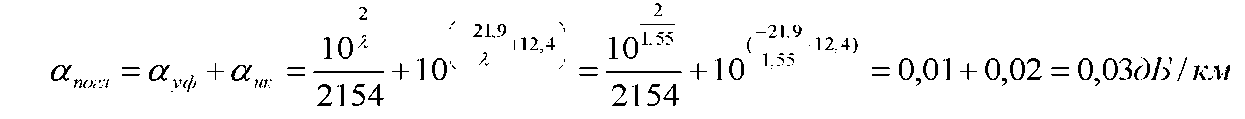 Суммарные потери: Это теоретический предел затухания на данной длине волны. Типичное значение α=0,22дБ/км обусловлен наличием микроизгибов. 2. Многомодовое ОВ (рек G.651 МСЭ-Т), с числовой апертурой NA= 0,3, имеет диаметр сердцевины d= 50 мкм и ПП n1 = 1,47 .Рассчитать потери на макроизгибах при RИЗГ= 5 см. Решение: 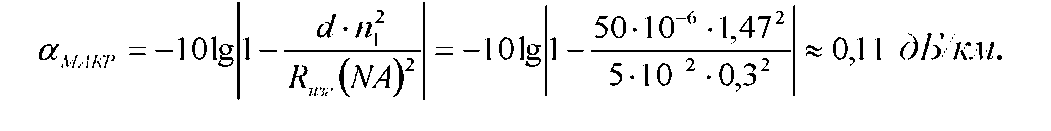 3. Одномодовое ОВ (рек G.652 МСЭ-Т) имеет следующие параметры: n1 = 1,46; NA= 0,12; d=8мкм, D=125 мкм. Рассчитать потери на микроизгибах, если высота микроизгибов h=0,2 мкм, а их число на 1км N=1. Решение: Потери на микроизгибах: 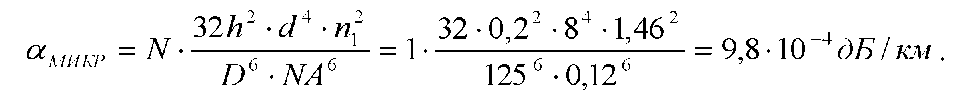 4. Одномодовое ОВ (рек. G.652) с параметрами n1 = 1,46; NA= 0,12; d=8мкм, D=125 мкм, имеет собственные потери 0,15 дБ/км. Определить допустимое значение числа микроизгибов на длине 1 км, если h=0,2 мкм. Решение: В соответствии с рек. G.652 затухание в ОВ должно быть не более 0,22дБ/км. Т.к. собственные потери составляют 0,15 дБ/км, то максимально допустимые потери на микроизгибах будут равны 0,22-0,15=0,07 дБ/км. Из формулы (2.18) выразим N, получим: 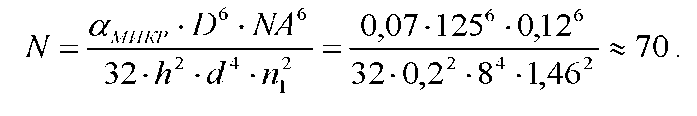 Задачи к разделу «Затухание в оптическом волокне» 1. Определить затухание света в ОВ обусловленное рэлеевским рассеянием, в 3-ем окне прозрачности при 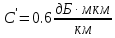 . сравнить с затуханием для 1-го и 2-го окон прозрачности. . сравнить с затуханием для 1-го и 2-го окон прозрачности.2. Рассчитать коэффициент затухания в ОВ на длине волны = 1310нм, n1 = 1,45 . Кабельные потери не учитывать. 3. Одномодовое ОВ (рек G.652 МСЭ-Т), с числовой апертурой NA= 0,12, имеет диаметр сердцевины d= 8 мкми ПП n1 = 1,46 .Рассчитать потери на макроизгибах при RИЗГ= 5 см. Построить график зависимости затухания от радиуса изгиба. 4. Одномодовое ОВ (рек. G.652 МСЭ-Т) с параметрами n1 = 1,46; NA= 0,12; d= 8 мкм,D=125 мкм, имеет собственные потери 0,15 дБ/км. Определить максимально допустимое значение h, если число микроизгибов на длине 1 км равно 50. Примеры решения задач к разделу 2 «Дисперсия оптического волокна. Полоса пропускания ОВ» 1. Рассчитать величину межмодовой дисперсии для МОВ с ГППП, СППП и оптимальным ППП. Для каждого случая определить коэффициент широкополосности. Исходные данные для расчета: n1 = 1,464, ∆= 0,013. Решение Для ОВ со ступенчатым ППП: 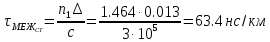 Для ОВ с градиентным ППП: 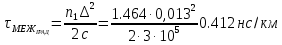 Для ОВ с оптимальным ППП: 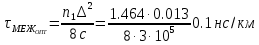 Определим коэффициент широкополосности: Для ОВ со ступенчатым ППП: 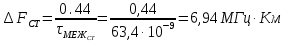 Для ОВ с градиентным ППП: 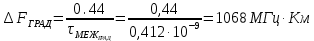 Для ОВ с оптимальным ППП: 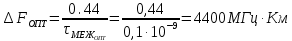 Как видно из полученных результатов, ОВ с ГППП значительно превосходит по техническим характеристикам ОВ со СППП. 2. Оптическое волокно имеет числовую апертуру NA=0,145. Рассчитать максимальный диаметр сердцевины, при котором соблюдается одномодовый режим, если ОВ работает на длине волны = 1,55мкм. Решение Значение максимального диаметра сердцевины ООВ вычислим, используя формулу (3.35): 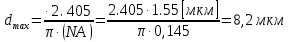 3. Определить возможность работы ОВ с числовой апертурой NA= 0.145 и диаметром сердцевины d=8 мкм, в одномодовом режиме, на средней длине волны С-диапазона, если погрешность изготовления диаметра сердцевины δd = ±0,5мкм. Решение 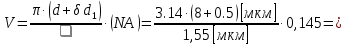 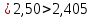 При наличии заданной погрешности изготовления волокно выйдет из одномодового режима, следовательно диаметр сердцевины должен быть уменьшен. 4. Рассчитать диаметр поля моды для ООВ при d= 9 мкм; NA=0,12; V= 2,189 на длине волны = 1,55 мкм. Решение Рассчитаем диаметр поля моды по формулам (2.32)-(2.35): 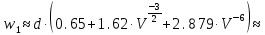 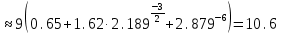 мкм 90.65+1.62 мкм 90.65+1.62; 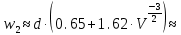 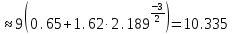 мкм мкм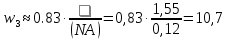 мкм мкм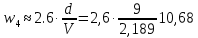 мкм мкм5. Рассчитать коэффициент широкополосности ∆F ООВ при В() = 20пс/нм∙ км,M()= 10пс/нм∙ км, ∆ = 0,1нм и L = 1км. Решение D()= M()+В()= 20 +10 = 30 пс / нм∙ км, 𝜏ХР() = ∆• D() • L = 0,1 • 30 • 1 = 3пс, ∆F = 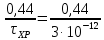 = 147 ГГц . = 147 ГГц .7. Оценить максимально допустимое расстояние оптического сегмента, на которое можно передать одноканальный сигнал с частотой В=100ГГц без ретрансляции, исходя из ограничений, вносимых поляризационной модовой дисперсией, если T = 1пс /√км. Решение На основании (2.48) получим: τPMD= 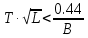 , ,Отсюда: 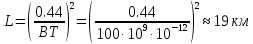 8. Вычислить наклон нулевой дисперсии, 0 = 1320 нм, = 1550 нм,D() = - 16,5пс / нм∙км. Решение Из выражения для удельной хроматической дисперсии следует, что наклон нулевой дисперсии (S0) определяется как 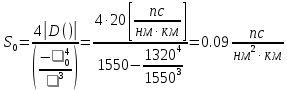 9. Выбрать тип модуля компенсации дисперсии, который необходимо включить в линейный тракт сети SDH, реализованной на основе стандартного ОВ (Rec. G. 652). Исходные данные Скорость передачи (STM-64) В=5Гбит/с рабочая длина волны =1,55мкм ширина спектра излучения на уровне 3 дБ ∆≤0,1 нм уровень мощности, вводимой в ОВ р1=0 дБм пороговая чувствительность рR= -30 дБм энергетический запас М=6 дБм Параметры ОК Коэффициент затухания α=0,25 дБ/км удельная хроматическая дисперсия D=20 пс/км∙нм средняя строительная длина l =2 км Параметры линейного тракта: Nрс =2; αрс=0,3 дБ; анс=0,1дБ. Решение: 1) Определим длину регенерационного участка по затуханию и дисперсии без учета компенсатора  Км Км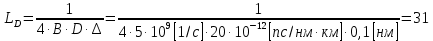 Км КмНеобходимо увеличить длину регенерационного участка по дисперсии так, чтобы она была сравнима с длиной регенерационного участка по затуханию; 2) Ближайшее значение компенсируемой модулем длины линии LDCравно 40 км; при этом общая длина компенсируемой линии LDсоставит 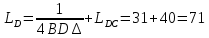 Км КмВыберем в качестве компенсатора модуль DCM - 40. Такой модуль вносит дополнительные потери aDC= 5 дБ. При этом длина регенерационного участка по затуханию будет составлять 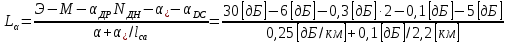 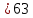 63ei Км  Пусть в качестве источника излучения используется более мощный (например, с уровнем вводимой мощности р1 = 3 дБм) и определим как изменится длина регенерационного участка по затуханию: Пусть в качестве источника излучения используется более мощный (например, с уровнем вводимой мощности р1 = 3 дБм) и определим как изменится длина регенерационного участка по затуханию: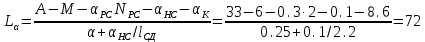 Км Км Следовательно, для увеличения длины регенерационного участка затуханию необходимо увеличить мощность ЛД в 2 раза либо увеличить чувствительность фотоприемника на 3 дБ. 10. Оценить максимальную длину регенерационного участка в линии с SMF волокном (Rec. G. 652) длиной 80 км и модулем DK - 80 для скорости передачи 10 Гбит/с (STM - 64). Решение: 1) Определим полную дисперсию, накопившуюся в линии: ∆τ = D∙L = 17[пс/нм ∙ км]∙ 80[км] = 1360пс/нм 2) Используя формулу (4.8), определим, на сколько процентов не скомпенсирована полная дисперсия на краю рабочего диапазона (С - диапазон: 1530 ÷ 1565 нм): NR(1530) = 1 + 16(1530 -1550)/1000 = 0,321 = 32% NR(1565) = 1 +16(1565 -1550)/1000 = 0,241 = 24% Видно, что на краю диапазона полная дисперсия не скомпенсирована примерно на 25%, что при полной дисперсии линии 1360 пс/нм составляет величину около 340 пс/нм. 3) Так как при скорости передачи 10 Гбит/с полная дисперсия в линии должна быть меньше 1000 пс/нм, то получаем, что длина этого участка может достигать 3 ∙ 80 км = 240 км. 11. Определить максимальную степень компенсации наклона дисперсионной кривой передающего ОВ типа DSF (Rec. G. 653), если в качестве компенсатора используется волокно DSCF (табл. 3). Решение: 1) По формуле RDS = S/D, определим коэффициент относительной крутизны дисперсионной кривой для ОВ типа DSF: на длине волны 1590 нм его дисперсия составляет 2,9 пс/нм∙км, а наклон дисперсионной кривой - 0,07 пс/нм2 ∙км 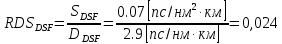 нм-1 нм-1Максимальную степень компенсации наклона обеспечивает DSCF компенсатор №3 из табл. .3 CКН=RDSdscf / RDSif= 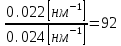 % % 12. Оценить возникающие потери, возникающие при соединении DSF волокна и отрезка SMF волокна. Решение: r 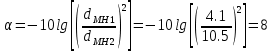 дБ дБЗадачи к разделу «Основные характеристики потерь и искажений сигналов в оптическом волокне» 1. Определить числовую апертуру и коэффициент широкополосности градиентного ОВ при n1=1.47; ∆= 0.01. 2. Рассчитать полосу пропускания ∆F для МОВ со ступенчатым ППП длиной 1 км при ∆ = 0.044; n1 = 1.465 и сравнить с градиентным. 3. Рассчитать коэффициент широкополосности ∆F градиентного ОВ при ∆= 0.01; n1 = 1.4654 и сравнить с оптимальным. 4. Рассчитать критическую длину волны при d=8 мкм, n1 = 1,445, ∆=0,004. 5. Рассчитать максимальный диаметр сердцевины, при котором соблюдается одномодовый режим, если = 1.6 мкм; NA = 0.12. 5. Рассчитать τХР, при М() = -10 пс/км∙нм; В() =20 пс/км∙нм, ∆= 0.1 нм; L = 1 км и определить реализуемую при этом максимальную скорость передачи. 6. Какой вид дисперсии 𝜏PMDили 𝜏CHR преобладает в SMF на = 1,55мкм если L = 49км, Т = 1пс/4кми ∆= 0,1нм. 7. Каково значение коэффициента хроматической дисперсии для Rec. G.652 на рабочей длине волны = 1620нм. 8. Каково соотношение 𝜏PMDи 𝜏CHR на длине L = 25км,если D() = 2пс/км∙нм, Т = 0,5пс/√км, ∆ = 0,05нм. 9. Определить АэффООВ на центральной длине волны C диапазона ( n1 = 1,45, n2 = 1,445 ). 10. Рассчитать 𝛕PMD и максимальную скорость передачи при: Т = 0,2пс/√км и L = 4 км. 11. Какова должна быть величина удельной хроматической дисперсии, чтобы обеспечить при скорости 10 Гбит/с длину линии связи L=50 км. (∆<<0.01)? 12. Используя данные таблицы 1 (вариант 2), определить тип модуля компенсации дисперсии, который необходимо использовать, если скорость передачи будет равна 10Гбит/с. 13. Оценить максимальную длину регенерационного участка в линии с SMF волокном (Rec. G. 652) длиной 60 км и модулем DK - 60 (см. таблицу2) для скорости передачи 10 Гбит/с (STM - 64). |
