Тренировка меры углов 1. Основные положения системы отсчетов и меры углов в артиллерии. Элементы вычислений
 Скачать 225.5 Kb. Скачать 225.5 Kb.
|
|
Основные положения системы отсчетов и меры углов в артиллерии. Элементы вычислений. 1.Деление угломера, его сущность, зависимость линейных и угловых величин. Формула тысячных. В артиллерии обычное измерение углов в градусах и минутах для практической работы неудобно – на боевой позиции некогда вести сложные расчеты, связанные с переходом от размеров цели или расстояний между различными целями к их видимой угловой величине в градусах или наоборот. Поэтому за единицу меры угловых величин в артиллерии принято деление угломера. Одно деление угломера – это центральный угол, соответствующий дуге в 1/6000 окружности (рис. 1). Длина дуги, соответствующей углу в одно деление угломера, равна: Поэтому деления угломера называются также «тысячными делениями» или сокращенно «тысячными». В  практике иногда применяют термины «малое деление угломера», «большое деление угломера». «Малым делением угломера» называют одно деление угломера (одну «тысячную дальности»). «Большим делением угломера» называют 100 делений угломера (100 «тысячных»). Так как окружность содержит 360о, или 360·60=21600/, то одно деление угломера равно: делений (одно «большое деление угломера») равны 3/,6·100 = 360/ = 6о. 1о = Формула тысячных. При системе измерения углов в «тысячных» существует простая зависимость между угловыми и линейными величинами, а именно: линейное расстояние между равноудаленными от наблюдателя точками равно угловому расстоянию между ними в делениях угломера, умноженному на 0,001 дальности. Эта зависимость выражается формулой: где А – линейное расстояние между точками; – угловое расстояние между точками в делениях угломера; Д – расстояние от наблюдателя до точек. при необходимости получения более точного результата найденную величину А увеличивают на 5%. 2. Определение дальности, угла, линейной величины предмета по формуле тысячных. Перевод делений угломера в градусы и минуты, перевод градусов и минут в деления угломера. Пример 1. Определить расстояние до рейки высотой 2 м при условии, что рейка видна под углом в 10 делений угломера. Решение. Пример 2. Расстояние между двумя целями, удаленными от батареи на 4200 м, равно 260 м. Определить угол в делениях угломера между этими целями. Решение. Пример 3. Угловое расстояние между двумя равноудаленными от наблюдателя предметами равно 25 делениям угломера. Определить линейное расстояние между этими предметами, если дальность Д до них равна 5000 м. Решение. Линейное расстояние между предметами будет равно Если требуется получить более точные расчеты, необходимо в полученный результат внести поправку на ошибку округления, т.е. увеличить результат на 5%: Окончательный результат: 125 + 6 = 131 м. Пример 4. Угловое расстояние между двумя равноудаленными от наблюдателя предметами равно 25 делениям угломера. Определить линейное расстояние между этими предметами, если дальность Д до них равна 5000 м. Решение. Линейное расстояние между предметами будет равно Если требуется получить более точные расчеты, необходимо в полученный результат внести поправку на ошибку округления, т.е. увеличить результат на 5%: Окончательный результат: 125 + 6 = 131 м. Пример 5. Определить расстояние до рейки высотой 2 м при условии, что рейка видна под углом в 10 делений угломера. Решение. Пример 6 . Расстояние между двумя целями, удаленными от батареи на 4200 м, равно 260 м. Определить угол в делениях угломера между этими целями. Решение. Аналогично определяются линейные размеры предмета, расстояние до которого известно. Чтение и запись углов вделениях угломера производят двумя способами. Первый способ - при записи отделяют черточкой тысячи и сотни от десятков и единиц, а при чтении произносят отдельно число сотен и число единиц. Если величина угла меньше 100 делений угломера или в ней отсутствуют десятки, то вместо сотен и десятков пишут и произносят «0» (ноль). В помещенной ниже таблице показано, как записывают и произносят различные углы, выраженные в делениях угломера:
Второй способ - чтение и запись углов производят как чтение и запись обычных чисел, добавляя в случае необходимости наименование меры угла, например, «влево15», «19 делений угломера», «635 тысячных». Для перевода величин углов, выраженных в делениях угломера, в величины, выраженные в градусах и минутах (и наоборот), пользуются соотношениями: 60-00 = 360°; 30-00 = 180°; 15-00 = 90°; 10-00 = 60°; 1-00 = 6°; 0-01 = 0°,06 = 3´,6. Перевод делений угломера в градусы и минуты, перевод градусов и минут в деления угломера. Для перевода величин углов, выраженных в делениях угломера в величины, выраженные в градусах и минутах и наоборот можно использовать следующие соотношения:
Однако на практике, при решении задач с помощью микрокалькуляторов, обычно данный перевод осуществляют следующим образом: а) перевод углов, выраженных в делениях угломера в градусы и минуты: например: 3-80 = 3,8 · 6о = 22о,8 = 22о 48/ б) перевод углов, выраженных в градусах и минутах в деления угломера: например: 35о24/ = 35о,4 : 6 = 5,9 = 5-90. При этом для перевода угловых минут и секунд в десятые и сотые доли градуса используют следующий прием: Пример 1.: Выразить в градусной мере угол 28о35/40//. Решение. 28о35/40// = 28о+35/ : 60 + 40// : 3600 = 28о+0,58о+0,01о = 28о,59 А для перевода долей градуса в минуты и секунды поступают так: Пример 2.: Представить в стандартном виде угол 46о,47, выраженный в градусной мере. Решение. 46о,47 = 46о+0,47 · 60 = 46о28/,2 46о28/,2 = 46о28/+0,2 · 60 = 46о28/12// 46о,47 = 46о28/12// система отсчетов в артиллерии Шкалы артиллерийских углоизмерительных приборов, как правило, нанесены в делениях угломера, причем большинство приборов имеет две шкалы - шкалу «грубого отсчета» (кольцо лимба), по которой считывают (устанавливают) число больших делений угломера, и шкалу «точного отсчета» (барабан или шкала микроскопа), по которой считывают (устанавливают) число малых делений угломера измеряемых (устанавливаемых) углов. Направление отсчета углов определяется в зависимости от того, что выражают собой эти углы; при этом могут быть два случая: а) углы отсчитываются от некоторой исходной линии в двух противоположных направлениях; б) углы отсчитываются от некоторой исходной линии только в одну сторону: либо по ходу часовой стрелки, либо против хода часовой стрелки. В первом случае углы рассматриваются как алгебраические величины и должны иметь соответствующие знаки: вправо - плюс, влево - минус (вверх - плюс, вниз - минус). Во втором случае углы знака не имеют, а при действиях с ними они рассматриваются как положительные величины. Для горизонтальных углов в артиллерии приняты две системы отсчета: а) по ходу часовой стрелки (шкала дирекционных углов) отсчитываются дирекционные углы и магнитные азимуты; б) против хода часовой стрелки (угломерная шкала) отсчитываются «угломеры», «отметки» и углы ветра. На шкалах артиллерийских углоизмерительных приборов, нанесенных по ходу часовой стрелки (стереодальномеры, буссоли, разведыпатсльные теодолиты, перископы), отсчету на приборе соответствует угол на местности (рис. 2), измеряемый в горизонтальной плоскости по ходу часовой стрелки от начального направления, которому соответствует отсчет «0», до направления оптической оси прибора в заданном направлении.  На шкалах артиллерийских углоизмерительных приборов, нанесенных против хода часовой стрелки (стереодальномеры, стереотрубы, буссоли, панорамы), отсчету на приборе соответствует угол на местности (рис. 3), измеряемый в горизонтальной плоскости против хода часовой стрелки от начального направления, которому, соответствует отсчет «0», до направления оптической оси прибора в данном направлении.  В соответствии с этим деления шкалы прибора с неподвижным указателем (орудийная панорама) оцифрованы походу часовой стрелки (рис.4); у приборов же с подвижным указателем (стереотруба) шкалы оцифрованы против хода часовой стрелки (рис. 5). 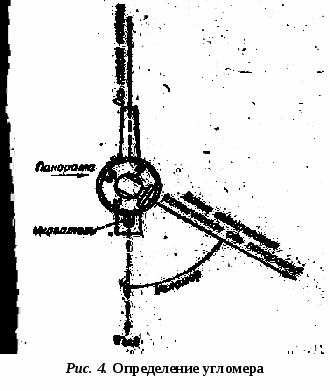 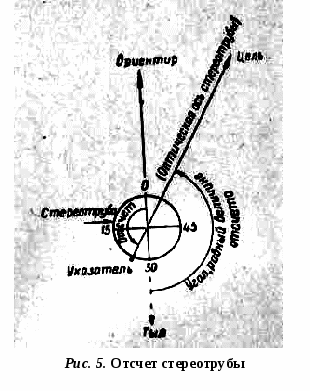 Угломером называется значение угла, устанавливаемого по шкалам угломерного кольца и барабана панорамы. Установке угломера соответствует угол в горизонтальной плоскости, отсчитываемый против хода часовой стрелки от линии, параллельной оси канала ствола и продолженной в «тыл» орудия (миномета) до направления оптической оси панорамы (рис. 4). Тот же угол, измеряемый на местности с помощью панорамы, называется «отметкой». Основной угломер - установка угломера, при которой после выполнения горизонтальной наводки ось канала ствола орудия (миномета) будет направлена в основном направлении. Отсчет прибора означает горизонтальный угол на местности между начальным направлением (продолжением направления линии 0-30 или 30-00) и направлением на цель (рис 6). 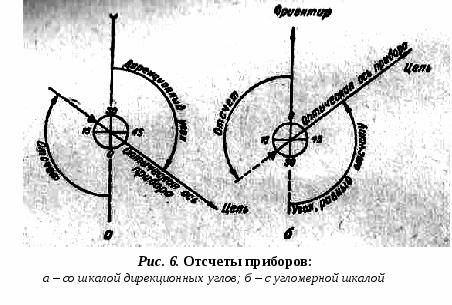 Основной отсчет - отсчет, при котором оптическая ось прибора направлена в ориентир, назначенный для ориентирования прибора, а линия 30-0 направлена в основном направлении. Установка угломера (отсчет) определяет направление наведенного орудия (прибора). Поэтому по величине установки угломера можно знать относительное расположение цели и точки наводки (рис. 7), а по отсчету - расположение цели относительно направления, в котором ориентирован прибор. 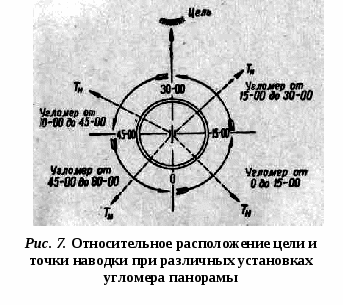 При измерении вертикальных углов и при вертикальной наводке орудия различают угол места цели (репера, ориентира), угол прицеливания и угол возвышения (рис. 8). 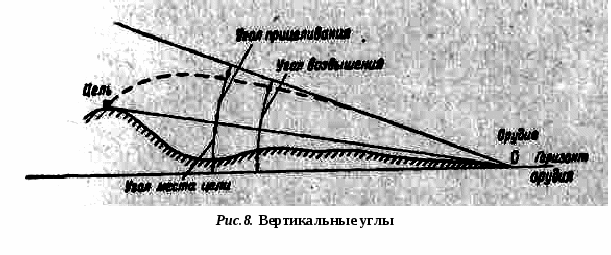 Углом места цели (репера, ориентира) называется угол в вертикальной плоскости между горизонтом орудия (прибора) и линией орудие (прибор) - цель. Углом прицеливания называется угол в вертикальной плоскости между линией орудие - цель и осью канала ствола наведенного орудия. Углом возвышения называется угол в вертикальной плоскости между горизонтом орудия и осью канала ствола наведенного орудия. Чтение и запись вертикальных углов, выраженных в делениях угломера, а также установок уровня производится так же, как мы с вами рассмотрели в первом вопросе данного занятия. А чтение и запись установок прицела по шкале «тысячных» производится так же, как чтение и запись обычных чисел. 3. Способы определения дальности, угловых и линейных величин в полевых условиях По карте.Для определения дальности по карте следует прочертить направление на цель. Для этого измеряют угол между ориентиром и целью или дирекционный угол цели, строят угол на карте и прочерчивают направление на цель. Затем изучают местность в этом направлении, сопоставляют ее с картой вдоль прочерченной линии и Определяют положение цели относительно рубежей, местных предметов и ориентиров, после чего на прочерченную линию наносят точку цели и определяют дальность до нее. Вычислением. Чтобы определить дальность до цели вычислением, необходимо знать линейную величину того или иного предмета, находящегося вблизи цели, затем измерить угловую величину предмета и по формуле зависимости линейных и угловых величин определить дальность. Линейные величины некоторых предметов, м
Пример. С наблюдательного пункта замечена пулеметная огневая точка вблизи телеграфного столба, угловая величина которого, измеренная биноклем, 0-08. Дальность до цели найдем по формуле С помощью ориентиров и рубежей, до которых известно расстояние или положение которых определено по карте. Пример. Наблюдательный пункт противника расположен на выс. «Песчаная». Дальность до выс. «Песчаная» определена по карте и равна 1800 м, следовательно, дальность до наблюдательного пункта 1800 м. Глазомерно. Чтобы определить дальность до цели глазомерно, необходимо знать видимость местных предметов на различных дальностях.
На слух. Слышемость различных звуков ночью
4. Порядок решения прямой и обратной геодезической задачи. Прямая геодезическая задача (ПГЗ) – это способ определения координат точки по известным прямоугольным координатам исходной точки, расстоянию между ними и дирекционному углу с исходной точки на определяемую. Дано: ХА, УА, АВ, (АВ) Найти: ХВ, УВ. Из рисунка видно, что ХВ=ХА + ΔХ, а УВ=УА + ΔУ. Из решения прямоугольного треугольника найдем приращение координат ΔХ=АВ·cos (АВ), ΔУ=АВ·sin (АВ) Поэтому: ХВ=ХА + АВ·cos (АВ) УВ=УА + АВ·sin (АВ) Х 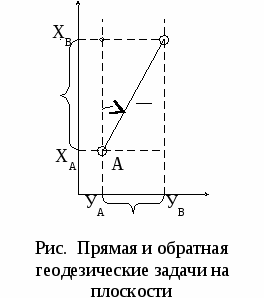 С В Х (АВ) АВ     У УУ Данные формулы являются математическим выражением прямой геодезической задачи. При решении ПГЗ необходимо учитывать знак приращений координат. Из рисунка видно: 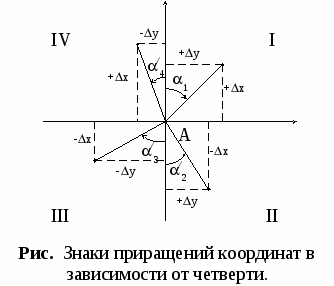 Х Х
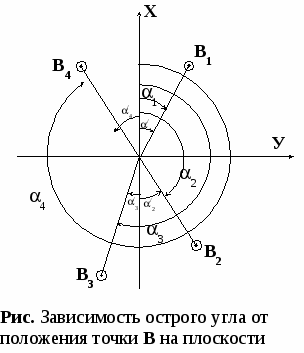
В1 У В3 В2 Поэтому при решении ПГЗ надо четко знать какой знак, в зависимости от дирекционного угла будет иметь приращение. При аналитическом решении ПГЗ приращение координат ΔХ и ΔУ определяются с помощью СТМ, артиллерийской логарифмической линейки (АЛЛ), микрокалькулятора, НИХ, таблиц логарифмов. Кроме того, ПГЗ можно решать с помощью курсопрокладчика, вычислителя 1В520 и ПУО. При решении ПГЗ на АЛЛ и СТМ необходимо знать, что к функции cos переходят следующим образом: cos = sin(15-00-). Также необходимо знать, что дирекционный угол к I четверти приводится следующим образом:
При решении ПГЗ на микрокалькуляторе, необходимо знать, что дирекционный угол предварительно необходимо перевести в градусы. О  братная геодезическая задача (ОГЗ) – это способ определения дирекционного угла (АВ) и расстояния АВ с одной точки на другую по известным прямоугольным координатам точек. братная геодезическая задача (ОГЗ) – это способ определения дирекционного угла (АВ) и расстояния АВ с одной точки на другую по известным прямоугольным координатам точек.Дано: ХА, ХВ, УА, УВ. Н  айти: АВ, (АВ) он же айти: АВ, (АВ) он же При решении ОГЗ в общем случае определяется не дирекционный угол (АВ) , а острый угол (АВ)' ', т.е. угол, приведенный к I четверти. Из решения прямоугольного треугольника определяется : '=arсtg где ΔУ = УВ – УА, ΔХ = ХВ – ХА Переход от (АВ)' к (АВ) осуществляется в зависимости от знаков приращения координат: Р  асстояние АВ = асстояние АВ =
При решении ОГЗ на артиллерийской логарифмической линейке (АЛЛ), дирекционный угол находится через угол : = аrсtg 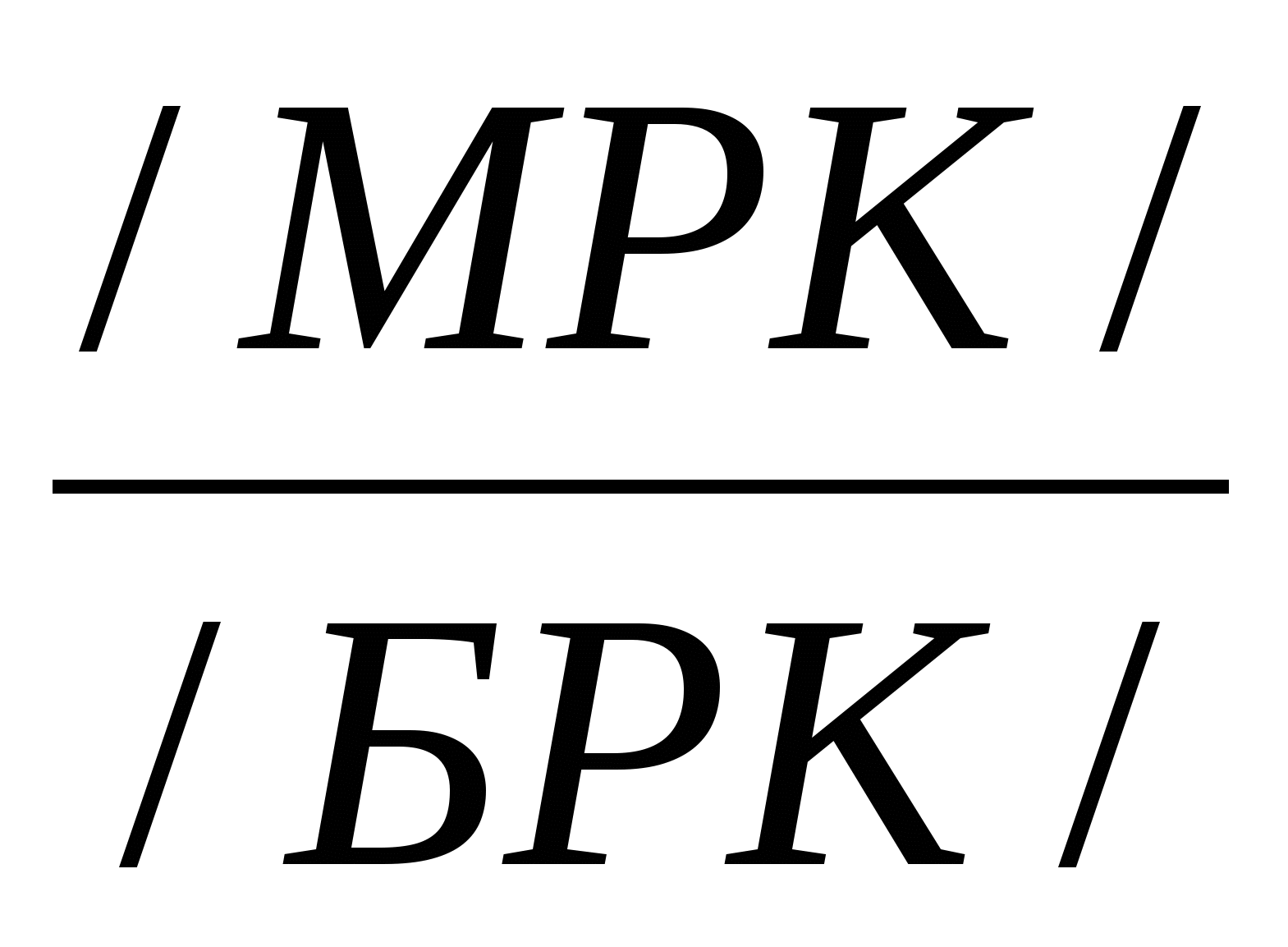 , где , гдеМРК – меньшая разность координат, а БРК – большая разность координат. Далее по таблице переводится в дирекционный угол
расстояния определяется как: 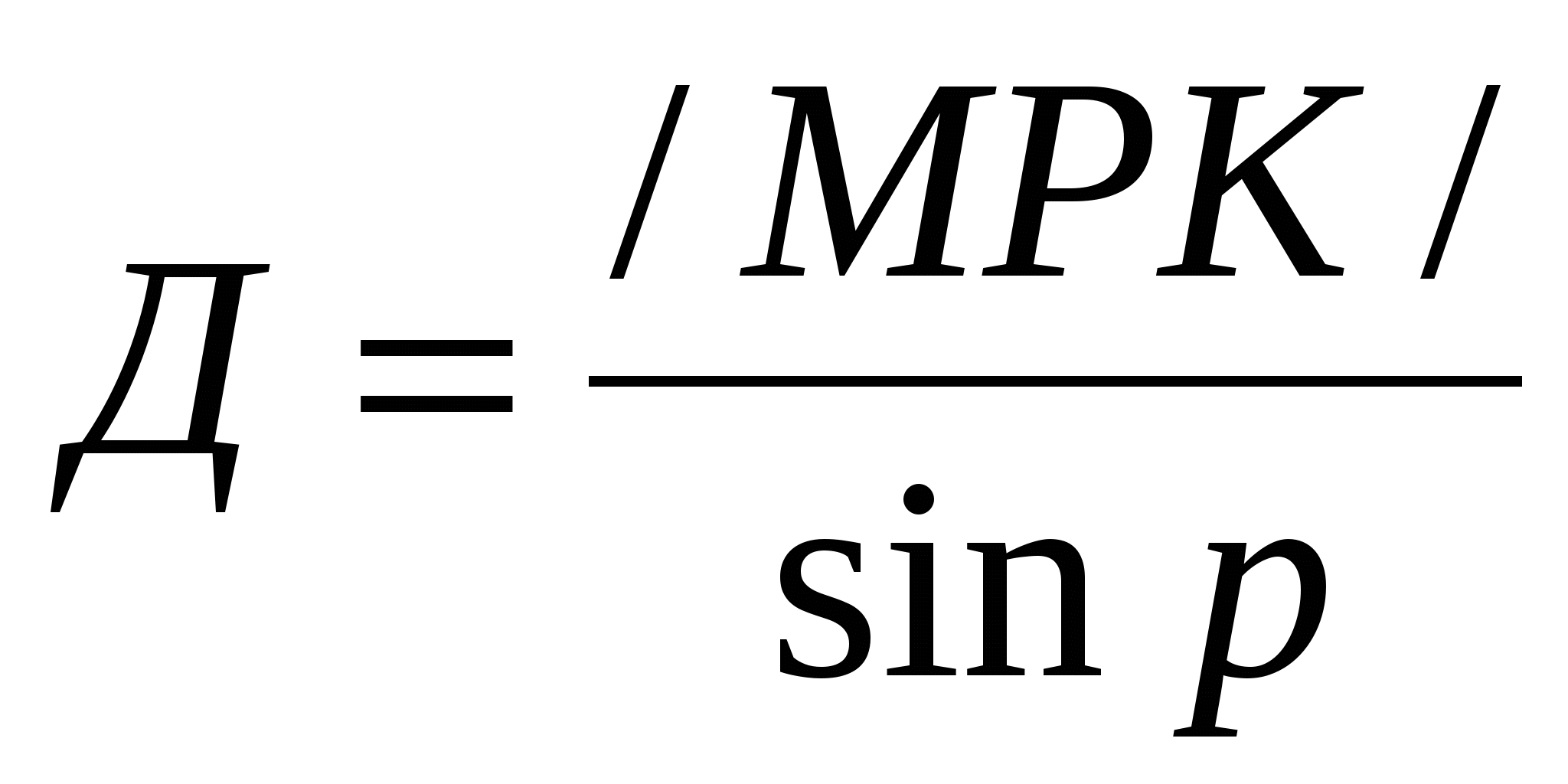 . .Решить ОГЗ можно с помощью таблиц логарифмов, АЛЛ, СТМ, микрокалькулятора, ПУО, вычислителя 1В520, таблиц Кравченко. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||