статья. Статья. Основные понятия теории уравнений и неравенств Прежде чем переходить к решению уравнений и неравенств, важно вспомнить теорию. Введём список основных понятий Уравнение равенство, содержащее в себе переменную, значение которой требуется найти.
 Скачать 145.99 Kb. Скачать 145.99 Kb.
|
|
Основные понятия теории уравнений и неравенств Прежде чем переходить к решению уравнений и неравенств, важно вспомнить теорию. Введём список основных понятий: Уравнение – равенство, содержащее в себе переменную, значение которой требуется найти. Корень (решение) уравнения – это значение переменной, при котором уравнение обращается в верное числовое равенство. Решить уравнение - найти его корни или доказать, что корней нет. Неравенство – два числа или математических выражения, соединенных одним из знаков: <, >, ≤, ≥. Основные свойства уравнений: Любой член уравнения можно перенести из одной части в другую, изменив его знак на противоположный. Обе части уравнения можно умножить или разделить на одно и то же число, не равное нулю. Решение неравенства – то значение неизвестного, при котором это неравенство обращается в верное числовое неравенство. Решить неравенство – найти все его решения или установить, что их нет. Методы решения уравнений и неравенств Теперь, после перечисления основных понятий, следует вспомнить известные нам из школьной программы способы решения уравнений и неравенств. Метод разложения на множители Для разложения на множители используют формулы сокращённого умножения (ФСУ), вынесение общего множителя за скобку, способ группировки, деление многочлена на многочлен. Суть данного метода в том, чтобы путем равносильных преобразований представить левую часть исходного уравнения, содержащую неизвестную величину в какой-либо степени, в виде произведения двух выражений, содержащих неизвестную величину в меньшей степени. При этом справа от знака равенства должен оказаться ноль. Метод замены переменной Цель данного метода в том, чтобы удачным образом заменить сложное выражение, содержащее неизвестную величину, новой переменной, в результате чего уравнение принимает более простой вид. Далее полученное уравнение решается относительно новой переменной, после чего происходит возврат к исходной переменной. Метод решения уравнений с помощью теоремы Виета Важно!!! Не ко всем квадратным уравнениям имеет смысл использовать эту теорему. Применять теорему Виета имеет смысл только к приведённым квадратным уравнениям. Приведенное квадратное уравнение – это уравнение, в котором старший коэффициент «a = 1». В общем виде приведенное квадратное уравнение выглядит следующим образом: х2 + px + q = 0. разница с обычным общим видом квадратного уравнения ax2 + bx + c = 0 в том, что в приведённом уравнении x2 + px + q = 0 коэффициент а = 1. Теорема Виета для приведённых квадратных уравнений «x2 + px + q = 0» гласит что справедливо следующее: х1 + x2 = −p, x1 · x1 = q, где x1 и x2 — корни этого уравнения. Нестандартные методы решения алгебраических уравнений и неравенств. Метод рационализации Приведем алгоритм решения уравнений и неравенств методом рационализации: Нахождение ОДЗ уравнения/неравенства Привести данное неравенство к стандартному виду: слева дробь (или произведение), справа – ноль. Заменить выражения левой части на более простые, эквивалентные им по знаку. Решить полученное неравенство, например, методом интервалов. Учёт ОДЗ Иногда знание ОДЗ позволяет доказать, что уравнение (или неравенство) не имеет решений, а иногда позволяет найти решение уравнения (или неравенства) непосредственно подстановкой чисел из ОДЗ. Приведём алгоритм решения уравнений и неравенств методом учёта ОДЗ: Найти ОДЗ уравнения/неравенства. Подставить значение ОДЗ в исходное уравнение/неравенство, чтобы проверить, является ли оно корнем. Метод мажорант (оценки) Этим методом можно решать нестандартные уравнения; уравнения повышенной сложности, например, уравнения в левой и правой части которой находятся функции, имеющие различную природу; уравнения или системы уравнений, в которых количество переменных превышает количество уравнений; задачи с параметром. Метод мажорант также называют методом оценки левой и правой частей, входящих в уравнения и неравенства. Мажорантой данной функции f(х) на множестве Р, называется такое число М, что либо f(х) ≤ М для всех х ϵ Р, либо f(х) ≥ М для всех х ϵ Р. Мажоранты многих элементарных функции известны. Их нетрудно указать, зная область значений функции. Приведём алгоритм решения уравнений и неравенств методом использования монотонности функции: Определить монотонность и область определения функции (ООФ). Методом подбора найти корень уравнения/неравенства. Исходя из монотонности функции делаем вывод о количестве корней. Использование графиков При решении уравнений и неравенств иногда полезно рассмотреть эскиз графиков их правой и левой частей. Тогда этот эскиз графиков поможет выяснить, на какие множества надо разбить числовую ось, чтобы на каждом из них решение уравнения (или неравенства) было очевидно. Обратим внимание, что эскиз графика лишь помогает найти решение, но писать, что из графика следует ответ, нельзя, ответ ещё надо обосновать. Приведём алгоритм решения уравнений и неравенств с помощью использования графиков: Определить ОДЗ уравнения/неравенства. Представить левую и правую части уравнения/неравенства как функции и построить их графики. По графику определить решение уравнения/неравенства. Доказать справедливость ответа. Угадывание корня уравнения Иногда внешний вид уравнения подсказывает, какое число является корнем уравнения. Приведём алгоритм решения уравнений методом угадывания корня: Методом подбора определить корень уравнения. Найти ОДЗ уравнения. Привести многочлен к стандартному виду. Определить остальные корни уравнения. Разработка интерактивного тренажера «Нестандартные методы решения уравнений и неравенств» В качестве продукта проекта был выбран интерактивный тренажер, который позволит практиковаться в решении уравнений и неравенств с помощью новых, нестандартных методов решения. Размещение тренажера на сетевой платформе позволит сделать данный продукт доступным для всех, кто хочет разобраться в этой теме. Анализ и характеристика сетевого сервиса, с помощью которого будет создаваться продукт При создании продукта были проанализированы следующие сетевые сервисы: LearningApps, Quizizz Wordwall, PurposeGames Платформы были проанализированы по критериям: Понятный и удобный интерфейс сайта Возможность составления разнотипных заданий, для создания интересного и разнообразного контента Наличие мобильной версии Возможность использования русского языка Возможность бесплатного использования ресурсов сетевого сервиса при создании и дальнейшем использовании тренажера Доступность (возможность быстрого распространения (с помощью ссылок, QR-кодов и т.п.) и использования) В данной таблице приведены результаты оценки сетевых сервисов по выбранным критериям:
В результате сравнения сетевых сервисов по указанным критериям для создания интерактивного тренажера была выбрана платформа LearningApps, которая соответствует наибольшему количеству требований. Во время создания проекта был проведен социальный опрос, целью которого было подтверждение актуальности выбранной темы и определение продукта проекта, который был бы интересен для потенциальной аудитории (учеников старшей школы). В результате были опрошены 16 человек, среди которых ученики 10-11 классов и студенты. В ходе опроса выяснилось, что 100% опрошенных часто сталкиваются с необходимостью решать уравнения и неравенства, при этом 38% из них сталкиваются с проблемами при решении таких заданий. 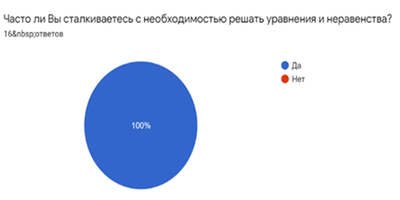  Также опрос показал, что самые распространенные проблемы при решении уравнений и неравенств среди учеников – проблема с выбором рационального решения и неочевидное решение. 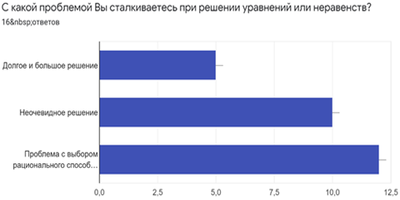 По результатам данной статистики можно сделать вывод о справедливости выдвинутой в данном исследовании проблемы. Кроме того, большинство опрошенных высказали желание узнать новые способы решения уравнений и неравенств, а также готовы практиковаться в данной теме. 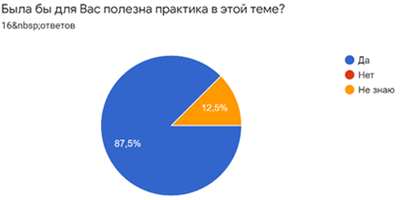  Результатами опроса подтвердился также выбор формата продукта. 75% опрошенных отметили, что им было бы удобно практиковаться в предложенной теме в формате онлайн- тренажера, что в итоге и было выбрано продуктом проекта. 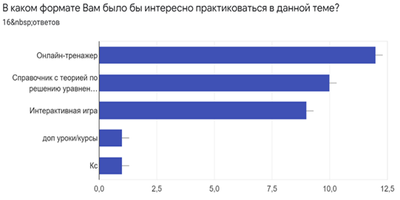 Подводя итог данной теме, стоит отметить, что использование нестандартных методов решения уравнений и неравенств, к сожалению, отодвигается на второй план, несмотря на то, что данные способы являются наиболее эффективными в решении. Именно поэтому необходимо изучать данные методы, ведь они в действительности являются незаменимыми при решении уравнений и неравенств. Список литературы Учебники: Ю. М. Колягин, М. В. Ткачева, Н. Е. Федорова, М. И. Шабунин. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс: базовый и углубленный уровни. 7-е изд. М.: Просвещение, 2019. – 384 с. Ю. М. Колягин, М. В. Ткачева, Н. Е. Федорова, М. И. Шабунин. Математика: алгебра и начала математического анализа. 11 класс: базовый и профильный уровни. 2-е изд. М.: Просвещение, 2010. – 336 с. Справочники: Олехник С.Н., Потапов М.К., Пасиченко П.И. Уравнения и неравенства. Нестандартные методы решения: справочник. 1997. – 219 с. Образовательные порталы: Образовательный портал для подготовки к экзаменам. Сдам ГИА: Решу ЕГЭ. ЕГЭ – 2021, Математика профильного уровня: задания, ответы, решения. Обучающая система Дмитрия Гущина. Задания: №13, №15. |
