УСЛОВИЕ (lab9_new). Отчет должен содержать 1 Титульный лист 2 Задание 3 Математическую модель 4 Таблицу внешних спецификаций

• Название: Отчет должен содержать 1 Титульный лист 2 Задание 3 Математическую модель 4 Таблицу внешних спецификаций
• Дата: 04.03.2019
• Размер: 364 Kb.
• Имя файла: УСЛОВИЕ (lab9_new).doc
• Тип: Отчет; #69525

Лабораторная работа 8. Работа с графикой в Delphi
Цель работы:

- научиться работать с графикой;

- научиться строить графики простейших функций с возможностью масштабирования;

- научиться выводить графики функций с использованием стандартной компоненты Chart;

- научиться строить графики функций, заданных в параметрическом виде;

- научиться воспроизводить эффект анимации.
Отчет должен содержать:

1) Титульный лист

2) Задание

3) Математическую модель

4) Таблицу внешних спецификаций

5) Иерархию модулей (подпрограмм)

6) Описание основных алгоритмов (словесное/блок-схема)

7) Проектирование тестов

8) Результаты тестирования (копии экрана)
Необходимые теоретические сведения для выполнения работы

(Источник: Языки программирования: конспект лекций по специальности 230400 "Информ. системы и технологии" / сост. О. И. Китаева;  – Иркутск: Изд-во ИрГТУ, 2012. – 1 o=электрон. опт. диск (CD-ROM.), сс. 51-57)

Графический инструментарий Delphi

1 Основа графики в Delphi

GDI - Graphics Device Interface в Windows представляет собой интерфейс, который Windows использует для рисования 2D графики. Это хотя и медленный способ отображения графики, однако, самый простой для понимания основ. Графические функции в Delphi являются надстройками над стандартными GDI функциями Windows.

Основу графики в Delphi представляет класс TCanvas – это холст (канва) с набором инструментов для рисования. Для работы с графикой определены классы TGraphic, TPicture, TGraphicObject, TCanvas. TGraphic – это абстрактный класс для инкапсуляции различных графических форматов, поддерживаемых Windows. Наследниками этого класса являются TBitmap, TIcon, TMetafile.

Класс TPicture представляет собой полнофункциональный класс, содержащий всё необходимое для работы с готовыми изображениями, является контейнером для класса TGraphic, позволяет загружать различные графические изображения, не заботясь о формате. Методы класса определяют тип изображения по расширению имени файла. Свойство Graphic класса TPicture указывает на тип используемого графического изображения.

Классы TGraphic и TPicture содержат ограниченное количество поддерживаемых ими форматов, однако на базе TGraphic можно создавать новые классы, которые будут поддерживать другие графические форматы.

Абстрактный класс TGraphicObjectявляется родительским по отношению к классам TFont, TBrush, TPen. Классы TFont, TBrush, TPen используются только в качестве свойств других классов.

Компонент TPaintBox используется в тех случаях, когда необходимо иметь прямоугольную область для выполнения графических операций. Использование этого компонента может быть альтернативой рисованию по канве формы, но TPaintBox не позволяет загружать готовые изображения.

2 Программное рисование

Форма и все визуальные управляющие компоненты Delphi обладают свойством Canvas. Конструктор Create создаёт экземпляр класса TCanvas со свойствами: Brush, Pen, Font, CopyMode, ClipRect, PenPos, Pixels.

Brush, Pen и Font называются инструментами для рисования.

Свойство PenPos – это текущая позиция карандаша – невидимый маркер, который задается горизонтальной PenPos.x и вертикальной PenPos.y координатами. Pixels[X,Y]: integer]:color представляет собой массив, содержащий цвета пикселей. Для доступа к отдельному пикселю достаточно указать его координаты.

Определим некоторые важные классы:

TPen. Используется для рисования простых линий. Обычно применяется для функции LineTo или при рисовании рамки для определённой фигуры (например для функции Rectangle).

TBrush. Кисть используется для заполнения области определённым цветом. Применяется в функциях Rectangle, FillRect или FloodFill.

TFont. Используется для задания шрифта, которым будет нарисован текст. Можно указать имя шрифта, размер и т.д.

TRegion. Позволяет задать регион (замкнутое пространство). Регионом может быть круг, квадрат или произвольная фигура.

Программное рисование рассмотрим на примере рисования цветка, растущего в траве.

Для рисования использованы классы TPen (Перо) и TBrush (Кисть) Изображение построено с помощью процедур Polygon (Многоугольник) и Ellipse (Эллипс). Процедуры заданы следующим образом:

procedure Polygon(Points: array of TPoint); Замкнутая ломаной линии – многоугольник задается как массив точек, последняя объявленная в массиве точка соединяется с первой и область внутри многоугольника закрашивается текущим цветом кисти.

procedure Ellipse(x1, y1, x2, y2: Integer); Эллипс вписан в прямоугольник, x1,y1 – координаты верхнего левого угла прямоугольника, x2,y2 - координаты нижнего правого угла.

Результат рисования представлен на рисунке 1.

Листинг программы
unit Unit1;

interface

uses

Windows, Messages, SysUtils, Classes, Graphics, Controls, Forms, Dialogs,

ExtCtrls, StdCtrls;

type

TForm1 = class(TForm)

Button1: TButton;

procedure Button1Click(Sender: TObject);

private

{ Private declarations }

public

{ Public declarations }

end;

const a:array[1..24] of integer=(95,-12,115,-32,75,-6,95,-26,115,-6,135,-26,95,14,75,-6,115,14,135,-6,95,22,115,2);

var

Form1: TForm1;

x1,y1,x2,y2:integer;

i,k,a1,a2,b1,b2:integer;

implementation

{$R *.DFM}

procedure TForm1.Button1Click(Sender: TObject);

begin

x1:=100;

y1:=100;

Refresh;

Canvas.pen.Color:=clBlack;

Canvas.Brush.Color:=$0000C400;

Canvas.Polygon([Point(x1, y1+80),Point(x1+200, y1+80),Point(x1+180, y1+60),Point(x1+170, y1+70),Point(x1+160, y1+60),Point(x1+150, y1+70)

,Point(x1+140, y1+60),Point(x1+130, y1+70),Point(x1+120, y1+60),Point(x1+110, y1+70),Point(x1+100, y1+60),Point(x1+90, y1+70),Point(x1+80, y1+60),Point(x1+70, y1+70)

,Point(x1+60, y1+60),Point(x1+50, y1+70),Point(x1+40, y1+60),Point(x1+30, y1+70),Point(x1+20, y1+60),Point(x1+10, y1+70)]);

Canvas.Polygon([Point(x1+100, y1+80),Point(x1+110, y1+80),Point(x1+110, y1+50),Point(x1+130, y1+30),Point(x1+110, y1+40),Point(x1+110, y1+10),Point(x1+105, y1-10)]);

Canvas.Brush.Color:=clYellow;

Canvas.Ellipse(x1+95,y1-15,x1+115,y1+5);

Canvas.Brush.Color:=$005B5BFF;

i:=1;

for k:=1 to 6 do

begin

Canvas.Ellipse(x1+a[i],y1+a[i+1],x1+a[i+2],y1+a[i+3]);

i:=i+4;

end;

end;

end.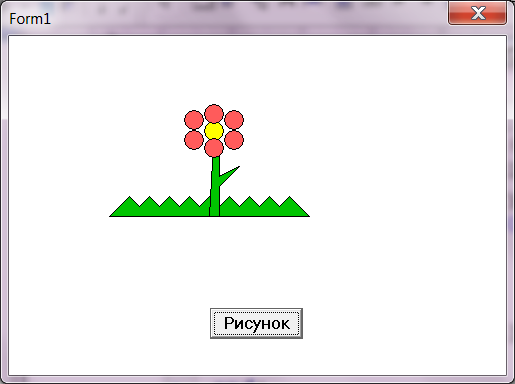


Рисунок 1 - Результат выполнения программы

3 Построение графиков функций. Преобразование координат

3.1 Вывод графика функции на экран

Построение графиков функций сопряжено с рядом особенностей использования 2D графики Delphi. Первая особенность состоит в выборе свойств канвы для прорисовки графика. Рисовать на канве можно разными способами. Первый вариант - использовать свойство канвы Pixels. Это свойство представляет собой двумерный массив, который отвечает за цвета канвы. Например, Canvas.Pixels[10,20] - соответствует цвету пикселя с координатами (10,20). Второй вариант - использовать свойство канвы Pen (перо), еще один вариант использовать в качестве точек графика окружности с радиусом 2-3 пикселя.

Вторая особенность построения графиков состоит в том, что точка, имеющая координаты (0,0) находится в верхнем левом углу экрана. Значения координаты по оси y увеличиваются на экране сверху вниз, поэтому, чтобы график функции выглядел на экране так, как привычно, человеческому глазу, необходимо выполнить преобразования координат.

Следующая особенность при построении графиков, так же связана с человеческим восприятием. График должен располагаться по всей площади экрана, отсюда возникает задача масштабирования.

Рассмотрим особенности построения 2D графика функции на примере. Применим для построения графика компонент PaintBox, для преобразования координат x и y используемфункции xp и yp, тогда для вывода графика произвольной функции F(x) достаточно написать следующий код:

With PaintBox1.Canvas do

begin

Brush.Color:=ClRed;

Pen.Color:=clRed;

While xdo

begin

Ellipse(xp(x),yp(F(x)),xp(x)+4,yp(F(x))+4);

x:=x+0.01;

end;

end;

Точки графика – окружности красного цвета, диаметром 4 пикселя.

3.2 Масштабирование графика

Очевидно, для построения графика и его масштабирования необходимо знать минимальные и максимальные значения координат x и y. В программе минимальное и максимальное значения x имеют идентификаторы xminиxmax, эти переменные нужно ввести в начале работы программы. Переменные yminиymax (минимальное и максимальное значение y) нужно вычислить, исходя из вида функции F(x). Вычисление можно выполнить с помощью следующей процедуры:

// Вычисление ymin и ymax

procedure min_max;

begin

x:=xmin;

ymax:=-1000;

ymin:=1000;

repeat

y:=F(x);

if y>ymax then ymax:=Y;

if ythen ymin:=Y;

x:=x+0.01;

until x>xmax;

end;

Решаем вопрос с масштабированием. Зная значения xmin,xmax, ymin, ymax, а также высотуHeight и ширинуWidth компонента PaintBox, определим коэффициенты масштабирования dx, по оси Ox и dyпо оси Оy, соответствующие действия выполнены в следующем фрагменте программы:

x:=xmin;

if x*xmax>0 then dx:=round(PaintBox1.Width/abs(xmax-x))

else dx:=round(PaintBox1.Width/(abs(xmax)+abs(x)));

dy:=PaintBox1.Height/(ymax-ymin);

Для программирования функций xp и yp, необходимо также, определить точку (a, b) начала координат, при выводе графика, с использованием компонента PaintBox, координаты этой точки определим с помощью следующих операторов присваивания:

a:=PaintBox1.Width div 2;

b:=PaintBox1.Height div 2;

3.3 Преобразование координат при построении графика

Теперь можно привести функции xp и yp, выполняющие преобразование координат:

function xp(x:extended):integer;

begin

xp:=round((x)*dx)+a;

end;

function yp(y:extended):integer;

begin

yp:=b-round((y)*dy);

end;

3.4 Порядок построения графика

Для составления компьютерной программы, решения задачи построения 2D графика функции можно рекомендовать следующий порядок действий:

• 
  проектируем главную форму программы, помещая на нее компоненты для управления действиями (меню, кнопки или др.) и компоненты для ввода граничных значений по оси Ox;
  
• 
  программируем вывод осей координат и вспомогательных надписей;
  
• 
  программируем вычисления значений функций, графики которых необходимо вывести на экран, их может быть несколько;
  
• 
  включаем в программу функции xp и yp, выполняющие преобразование координат и процедуру вычисления yminиymax;
  
• 
  программируем процедуру вывода графиков, используя приведенные выше фрагменты исходного кода.
  

Приведенный порядок построения графика проиллюстрируем на следующем примере: выведем график функции y=+10.

В левой части рис.2 показан проект формы для вывода графика (использованы компоненты PaintBox1, MainMenu1, Edit1, Edit2, Label1, Label2), в правой части рисунка – результат выполнения пункта меню «Оси координат».



Рисунок 2 – Последовательность построения графика
Для построения осей координат использована следующая процедура:
//вывод координатной сетки

procedure TForm1.N1Click(Sender: TObject);

var i,n,x,y:integer;

begin

With Form1.PaintBox1.Canvas do

begin

n:=round(Width/20);

Pen.Style:=psDashDot;

X:=0; Y:=0;

For i:=1 to n do

begin

MoveTo(x,y);

LineTo(Width ,y);

y:=y+20;

end;

Y:=0;

For i:=1 to n do

begin

MoveTo(x,y);

LineTo(x ,PaintBox1.Height);

x:=x+20;

end;

//вывод осей координат

Pen.Style:=psSolid;

Pen.Mode:=pmBlack;

Pen.Width:=2;

MoveTo(PaintBox1.Width div 2,0);

LineTo(PaintBox1.Width div 2,Height);

MoveTo(0,PaintBox1.Height div 2);

LineTo(PaintBox1.Width,PaintBox1.Height div 2);

//стрелки

MoveTo(PaintBox1.Width div 2,0);

LineTo(PaintBox1.Width div 2-5,15);

MoveTo(PaintBox1.Width div 2,0);

LineTo(PaintBox1.Width div 2+5,15);

MoveTo(PaintBox1.Width,PaintBox1.Height div 2);

LineTo(PaintBox1.Width-15,PaintBox1.Height div 2-5);

MoveTo(PaintBox1.Width,PaintBox1.Height div 2);

LineTo(PaintBox1.Width-15,PaintBox1.Height div 2+5);

//надписи

TextOut(380,175,'x');

TextOut(180,0,'y');

TextOut(185,200,'0');

end;

end;
Результат построения графика показан на рис.3.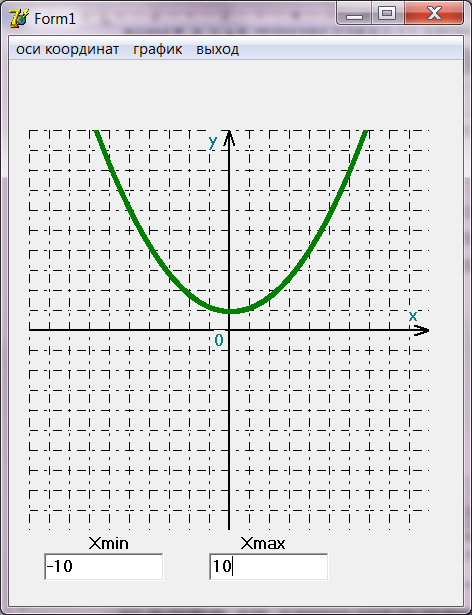


Рисунок 3 – Результат построения графика
4 Индивидуальные задания

Лабораторная работа включает 4 задания.
4.1.1 Построить графики четырех функций (табл. 1). Все графики построить различными цветами (точки/линии графика выводятся в цикле). Предусмотреть масштабирование графика. Интервал изменения аргумента, цвет графика должны задаваться пользователем.

4.1.2 Построить графики тех же функций с использованием компонент Chart с несколькими сериями Series и ColorBox для выбора цвета линий).

Таблица 1 – Варианты заданий для построения графиков функций

Вариант	f1(x)	f2(x)	f3(x)	f4(x)
	cos(x)	2cos(x)	cos(2x)	cos(x/2)
	sin(x)	2sin(x)	sin(2x)	sin(x/2)
	ex	e-x	e2x	ex/2
	x2	-x2	аx2	x2+2
	ln(x)	ln(2x)	ln(x/2)	ln(x)/2
	x3	2x3	x3/2	(x/2)3
	ln(x)	2ln(x)	ln(x2)	(ln(x))2
	ex	ex/2	ex-1	e2x
	cos(x)	Cos(x/2)	(cos(x))2	cos(2x)
	sin(x)	sin(x/2)	(sin(x))3	(sin(x))2
	x3	x3+2	2x3	2x3+2
	x2	3x2	x2/3	x2+3
	x3	2x3	x3/2	x3+2
	xsin(x)	x/2sinx	xsin(x)2	xsin(2x)
	x-sin(x/2)	x-2sinx	x-sin(2x)	x-sin(x)
	x-cosx	x-cos(2x)	x-cos(x/2)	x-cos(3x)

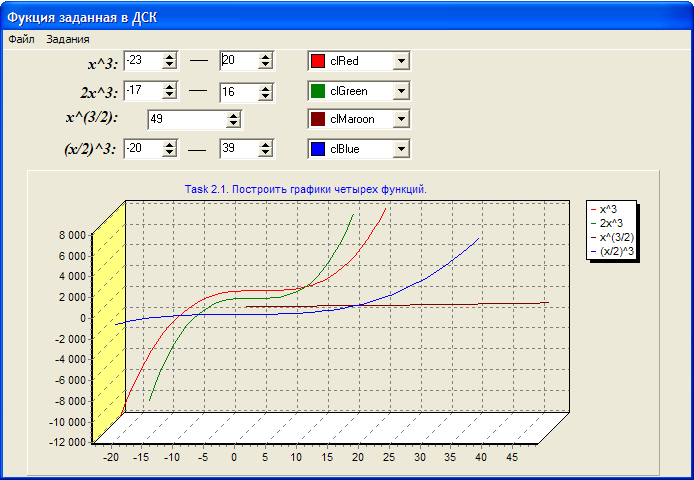Рисунок 4 – Пример результата 4.1.2
4.2. Построить график функции, заданной в параметрическом виде. Цвет, значение параметра (-ов), диапазон, и шаг изменения угла задаются пользователем.

1. Улитка Паскаля: , , , , . Рассмотреть случаи, когда , , .

2. Кардиоида: , , , .

3. Эпициклоида: , , a, b>0, . Рассмотреть случай, когда есть целое положительное число, ;

4. Астроида: , , .

5. Строфоида: , , , .

6. Конхоида Никомеда: , ; правая ветвь – , левая – ; , . Рассмотреть случаи, когда , ,.

7. Строфоида: , , , .

8. Циссоида: , , , .

9. Построить спираль вокруг начала координат с N витками и внешним радиусом R; начальное направление спирали образует с осью OX угол . Параметрическое представление спирали: ,,,.

10. Кардиоида: , , , .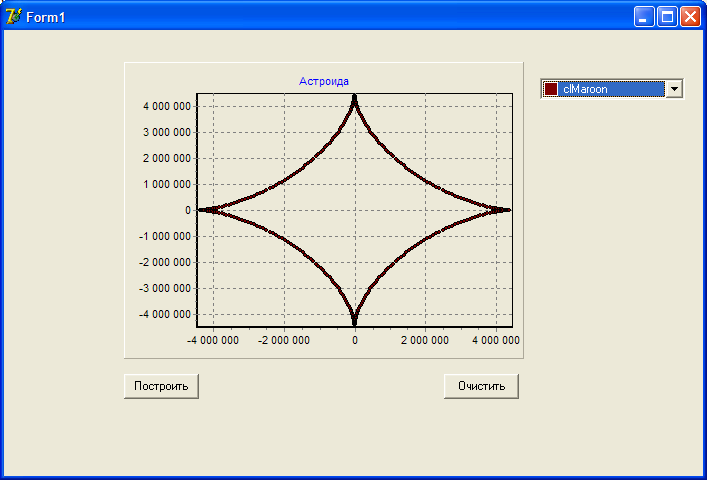


Рисунок 4 – Пример результата 4.2 (Астроида)
4.3. Анимация графических объектов. На канве главной формы обеспечить движение объекта.

1. 
   Изобразить на экране точку, движущуюся по окружности с постоянной угловой скоростью.
   
2. 
   Составить программу для управления скоростью движения точки по окружности. Управление производится пользователем путем нажатия соответствующих кнопок.
   
3. 
   Изобразить на экране две движущиеся точки, траектории которых являются концентрическими окружностями. Угловая скорость точки, движущейся по внутренней окружности, несколько меньше, чем угловая скорость точки, движущейся по внешней окружности (обе скорости – постоянные величины). При этом:
   

• 
  обе точки вращаются в одном направлении (например, по часовой стрелке);
  
• 
  точки вращаются в противоположных направлениях.
  

4. 
   Изобразить на экране правильный треугольник, вращающийся в плоскости экрана вокруг своего центра.
   
5. 
   Написать программу, которая выводит изображение вращающегося велосипедного колеса.
   
6. 
   Обеспечить движение по экрану слова, введенного пользователем, по горизонтали – от левого края к правому и обратно.
   
7. 
   Изобразить на экране правильный треугольник, вращающийся в плоскости экрана вокруг своего центра.
   
8. 
   Обеспечить движение по экрану окружности от верхнего края к нижнему и обратно.
   
9. 
   Написать программу, которая выводит изображение секундомера с двигающейся секундной стрелкой.
   
10. 
    Обеспечить движение по экрану слова, введенного пользователем, по вертикали – от верхнего края к нижнему и обратно.
    
11. 
    Изобразить на экране квадрат, вращающийся в плоскости экрана вокруг своего центра.
    

4.4. Используя компоненты Image и Timer (событие OnTimer, возникающее через заданный интервал Interval компоненты Timer) организовать смену картинок, загружаемых из созданных графических файлов, сформировать анимационный ролик (например, летящую птицу, движущиеся облака, летающую тарелку, растущий цветок и т.п.).

Примечание: желательно создаваемые графические файлы именовать номерами (1.bmp, 2.bmp…). Загрузка очередного файла производится путем применения метода загрузки картинки при возникновении события OnTimer: Image1.Picture.LoadFromFile(IntToStr(i)+'.bmp'). В обработчике этого же события следует менять значение i = 0..Количество файлов.