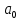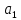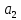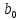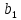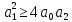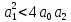Отчет по лабораторной ТАУ Типовые звенья и их характеристики. Отчет к лабораторной работе №1 по дисциплине «Теория и системы у. Отчет к лабораторной работе 1 по дисциплине Теория и системы управления Типовые звенья и их характеристики
 Скачать 277.84 Kb. Скачать 277.84 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР) Кафедра компьютерных систем в управлении и проектировании (КСУП) ОТЧЕТ к лабораторной работе №1 по дисциплине «Теория и системы управления»: Типовые звенья и их характеристики Выполнил Студент гр. 587-2 _________ Дагба К. Б.-Б. «___» _____________ 2019 г. Проверил: Ст. научный сотрудник, к.т.н. ___________ Карпов А. Г. «___» _____________ 2019 г 1 ВведениеЦель работы Целью данной работы является изучение моделей и характеристик основных типовых звеньев и ознакомление с моделирующей установкой РВЛ ТАУ. Основные соотношения Функциональные элементы, применяемые в САУ, могут иметь самое разное конструктивное исполнение и принцип действия. Но общность их математического описания позволяет выделять из их множества ограниченное число так называемых типовых звеньев. К типовым звеньям относят звенья, описываемые дифференциальными уравнениями не выше второго порядка, т. е. звенья нулевого, первого и второго порядков. В общем виде уравнение второго порядка выглядит следующим образом: 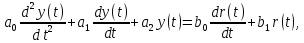 где y(t) – выход звена, а r(t) – вход звена. Названия наиболее часто используемых звеньев и их параметры приведены в таблицы 1.1. Таблица 1.1 – Типовые звенья и их параметры.
1.3 Задание1. Путем выполнения простейших экспериментов познакомиться с функциональными возможностями используемых в лабораторной работе инструментальных средств – цифрового электронного модуля РВЛ, включающего в себя: осциллограф, панель управления каналами осциллографа, регулятор уровня синхронизации, sin–генератор, импульсный генератор. 2. Для каждого звена (см. табл. 1.1) по его передаточной функции записать операторное уравнение. 3. По передаточной функции каждого звена построить его временные (функцию веса и переходную функцию) и частотные характеристики – ЛАЧХ, ФЧХ и АФЧХ. 4. Для инерционных звеньев по логарифмическим частотным характеристикам определить частоты сопряжения и среза. 5. Определить значение полюсов и нулей передаточных функций звеньев и оценить их влияние на характер переходного процесса. 2 Ход работыСоставим дифференциальные уравнения для соответствующих звеньев: – безынерционное звено: 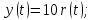 – апериодическое звено первого порядка: 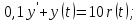 – апериодическое звено второго порядка: 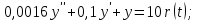 – колебательное звено: 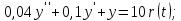 – идеальное интегрирующее: 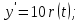 – интегрирующее звено с замедлением: 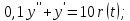 – идеальное дифференцирующее: 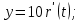 – дифференцирующее с замедлением звено: 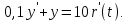 Согласно имеющемуся заданию, произведем расчет простейших звеньев. 2.1 Безынерционное (усилительное) звено Произведем замену 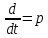 , чтобы перейти к операторному уравнению, получим: , чтобы перейти к операторному уравнению, получим: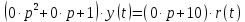 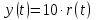 Передаточная функция: W(p) = F(p) / F1(p) = K = 10. Весовая (импульсная переходная) функция: w(t) = h'(t) = 0. На рисунке 2.1 представлен график весовой функции. 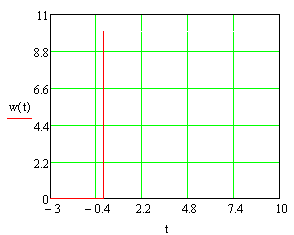 Рисунок 2.1 – График весовой функции На рисунке 2.2 представлен график переходной характеристики.  Рисунок 2.2 – График переходной характеристики Фазовая частотная характеристика (ФЧХ): 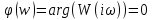 На рисунке 2.3 представлен график ФЧХ.  Рисунок 2.3 – График ФЧХ Логарифмическая амплитудная частотная характеристика (ЛАЧХ): 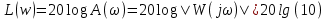 На рисунке 2.4 представлен график ЛАЧХ.  Рисунок 2.4 – График ЛАЧХ Амплитудно-фазовая частотная характеристика (АФЧХ): 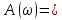 10 10На рисунке 2.5 представлен график АФЧХ. 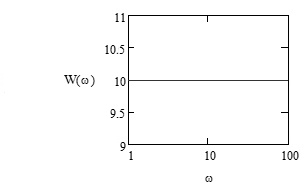 Рисунок 2.5 – График АФЧХ 2.2 Апериодическое звено 1-го порядка Произведем замену 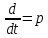 , чтобы перейти к операторному уравнению, получим: , чтобы перейти к операторному уравнению, получим: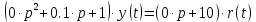 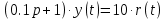 Передаточная функция:  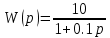 Весовая функция: 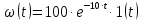 На рисунке 2.6 представлена весовая функция. 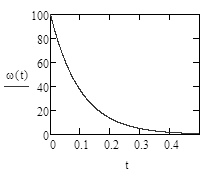 Рисунок 2.6 – График весовой функции На рисунке 2.7 представлена переходная характеристика. 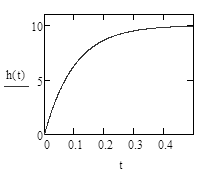 Рисунок 2.7 – График переходной характеристики Амплитудная частотная характеристика (АЧХ): 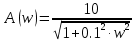 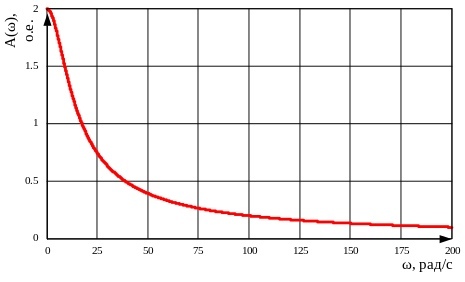 На рисунке 2.8 представлен график АЧХ. На рисунке 2.8 представлен график АЧХ.Рисунок 2.8 – График АЧХ Фазовая частотная характеристика (ФЧХ): 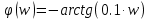 На рисунке 2.9 представлен график ФЧХ. 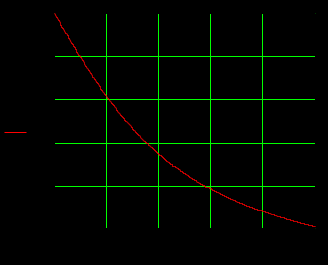 Рисунок 2.9 – График ФЧХ Логарифмическая амплитудно-частотная характеристика (ЛАЧХ): 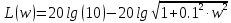 На рисунке 2.10 представлен график ЛАЧХ. 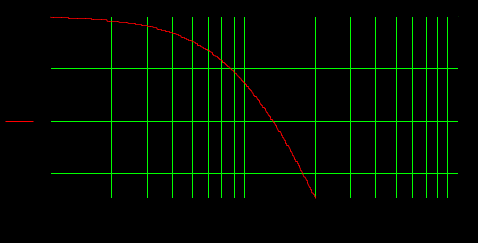 Рисунок 2.10 – График ЛАЧХ Амплитудно-фазовая частотная характеристика (АФЧХ): 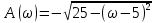 На рисунке 2.11 представлен график АФЧХ. 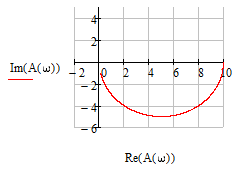 Рисунок 2.11 – График АФЧХ 2.3 Апериодическое звено 2-го порядка Произведем замену 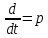 , чтобы перейти к операторному уравнению, получим: , чтобы перейти к операторному уравнению, получим: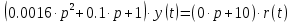 ( 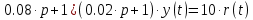 Передаточная функция: 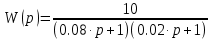 Весовая (импульсная переходная) функция: w(t): 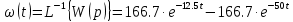 На рисунке 2.12 представлен график весовой функции. 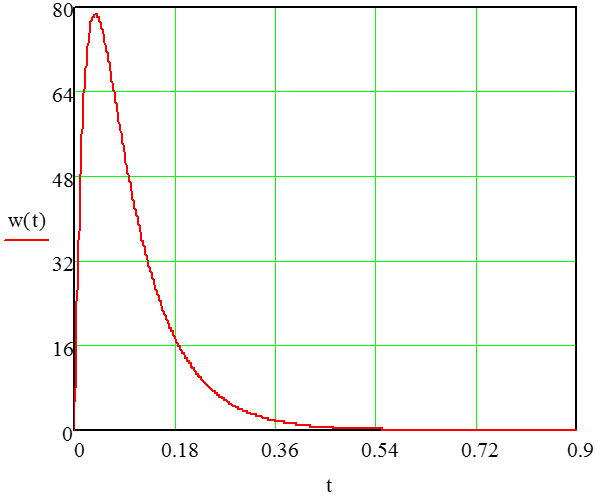 Рисунок 2.12 – График весовой функция Переходная характеристика: 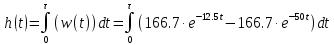 На рисунке 2.13 представлен график переходной характеристики. 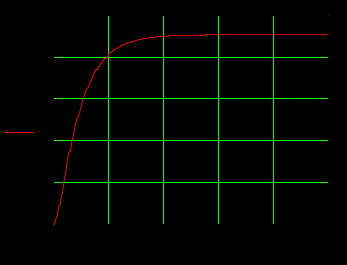 Рисунок 2.13 – График переходной характеристики Амплитудная частотная характеристика (АЧХ): 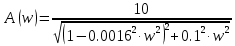 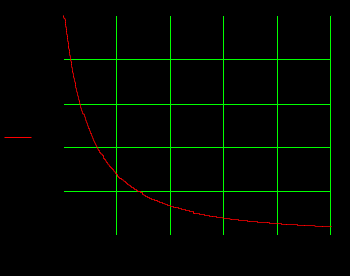 На рисунке 2.14 представлен график АЧХ. На рисунке 2.14 представлен график АЧХ.Рисунок 2.14 – График АЧХ Фазовая частотная характеристика (ФЧХ): 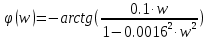 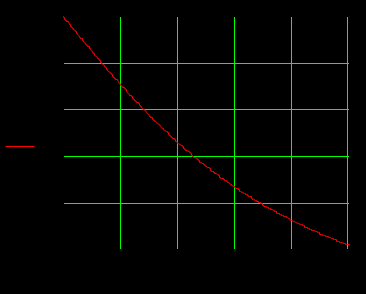 На рисунке 2.15 представлен график ФЧХ. На рисунке 2.15 представлен график ФЧХ.Рисунок 2.15 – График ФЧХ Логарифмическая амплитудно-частотная характеристика (ЛАЧХ): 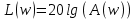 На рисунке 2.16 представлен график ЛАЧХ. 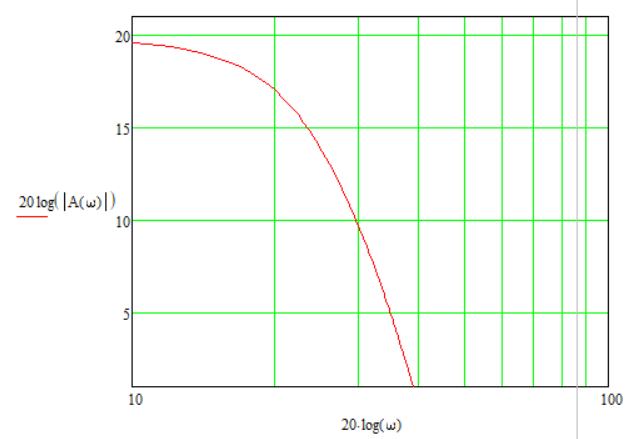 Рисунок 2.16 – График ЛАЧХ Амплитудно-фазовая частотная характеристика (АФЧХ): 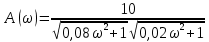 На рисунке 2.17 представлен график АФЧХ. 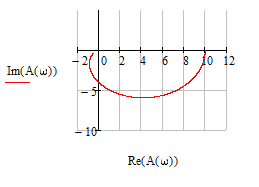 Рисунок 2.17 – График АФЧХ 2.4 Колебательное звено Произведем замену 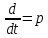 , чтобы перейти к операторному уравнению, получим: , чтобы перейти к операторному уравнению, получим: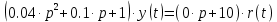 Передаточная функция: 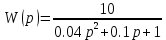 Весовая функция: 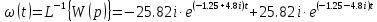 На рисунке 2.18 представлена весовая функция. 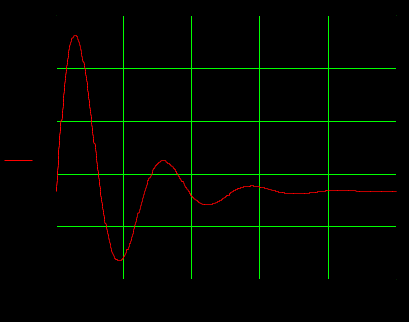 Рисунок 2.18 – График весовой функции Переходная характеристика: 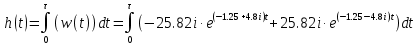 На рисунке 2.19 представлена переходная характеристика. 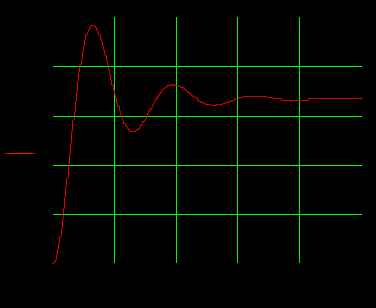 Рисунок 2.19 – График переходной характеристики Амплитудная частотная характеристика (АЧХ): 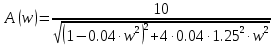 На рисунке 2.20 представлен график АЧХ. 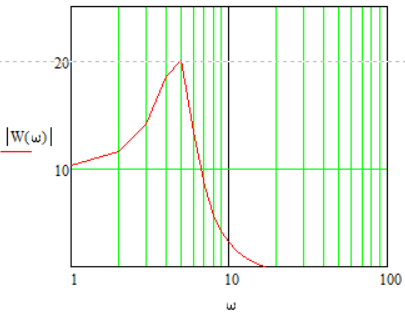 Рисунок 2.20 – График АЧХ Фазовая частотная характеристика (ФЧХ): 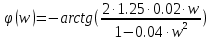 На рисунке 2.21 представлен график ФЧХ. 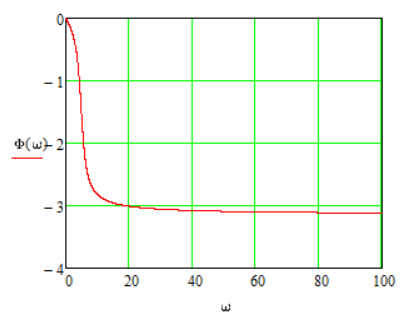 Рисунок 2.21 – График ФЧХ Логарифмическая амплитудно-частотная характеристика (ЛАЧХ): 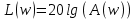 На рисунке 2.22 представлен график ЛАЧХ. 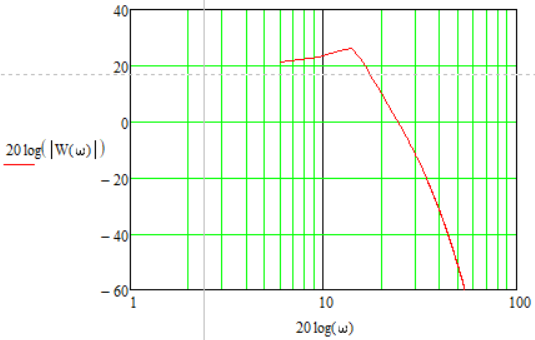 Рисунок 2.22 – График ЛАЧХ Амплитудно-фазовая частотная характеристика (АФЧХ): 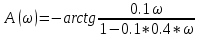 На рисунке 2.23 представлен график АФЧХ. 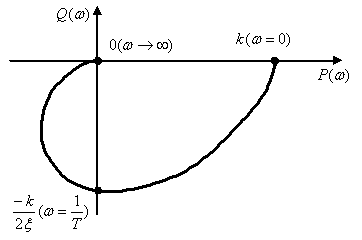 Рисунок 2.23 – График АФЧХ 2.5 Идеально интегрирующее звено Произведем замену 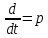 , чтобы перейти к операторному уравнению, получим: , чтобы перейти к операторному уравнению, получим: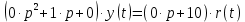 Передаточная функция: 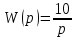 Весовая функция: 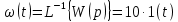 На рисунке 2.24 представлен график весовой функции. 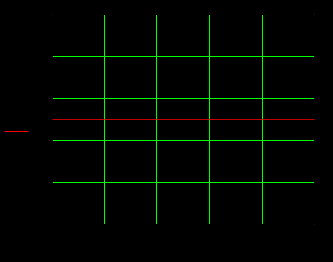 Рисунок 2.24 – График весовой функции Переходная характеристика: 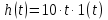 На рисунке 2.25 представлен график переходной характеристики. 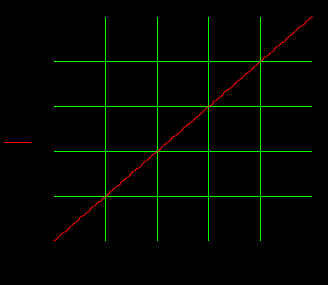 Рисунок 2.25 – График переходной характеристики Амплитудная частотная характеристика (АЧХ): 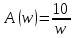 На рисунке 2.26 представлен график АЧХ. 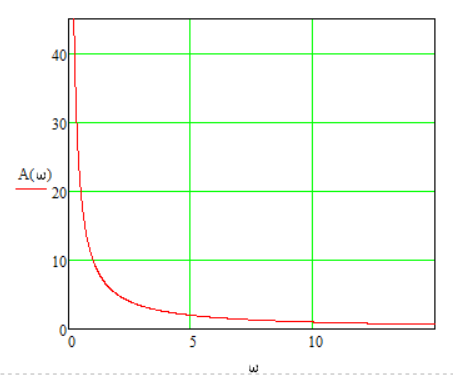 Рисунок 2.26 – График АЧХ Фазовая частотная характеристика (ФЧХ): 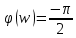 На рисунке 2.27 представлен график ФЧХ. 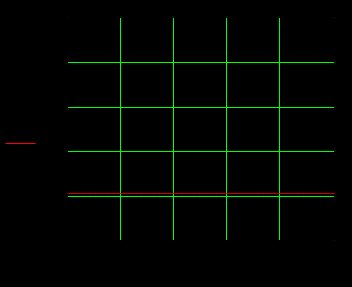 Рисунок 2.27 – График ФЧХ Логарифмическая амплитудно-частотная характеристика (ЛАЧХ): 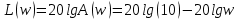 На рисунке 2.28 представлен график ЛАЧХ. 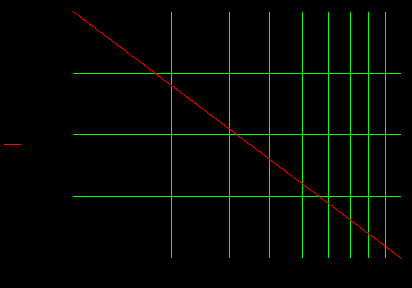 Рисунок 2.28 – График ЛАЧХ Амплитудно-фазовая частотная характеристика (АФЧХ): 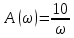 На рисунке 2.29 представлен график АФЧХ. 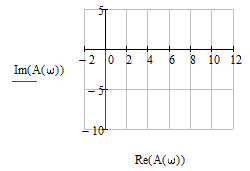 Рисунок 2.29 – График АФЧХ 2.6 Интегрирующее звено с замедлением Произведем замену 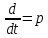 , чтобы перейти к операторному уравнению, получим: , чтобы перейти к операторному уравнению, получим: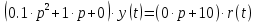 Передаточная функция: 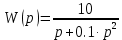 Весовая функция: 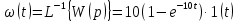 На рисунке 2.30 представлен график весовой функции. 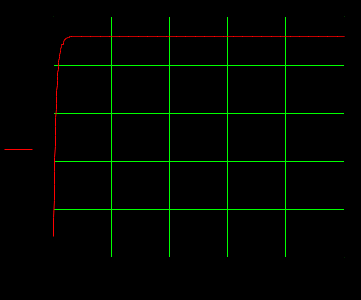 Рисунок 2.30 – График весовая функции Переходная характеристика: 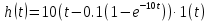 На рисунке 2.31 представлен график переходной характеристики. 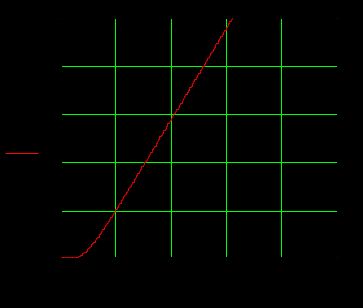 Рисунок 2.31 – График переходной характеристики Амплитудная частотная характеристика (АЧХ): 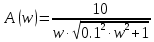 На рисунке 2.32 представлен график АЧХ. 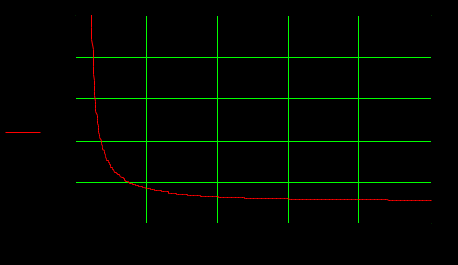 Рисунок 2.32 – График АЧХ Фазовая частотная характеристика (ФЧХ): 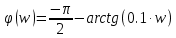 На рисунке 2.33 представлен график ФЧХ. 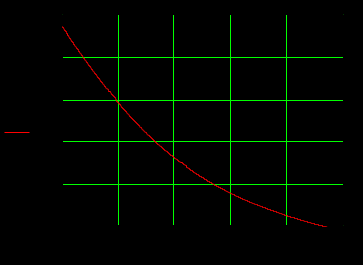 Рисунок 2.33 – График ФЧХ Логарифмическая амплитудно-частотная характеристика (ЛАЧХ): 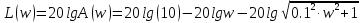 На рисунке 3.34 представлен график ЛАЧХ. 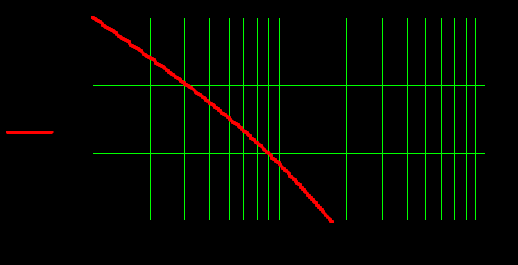 Рисунок 3.34 – График ЛАЧХ Амплитудно-фазовая частотная характеристика (АФЧХ): 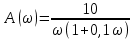 На рисунке 2.35 представлен график АФЧХ. 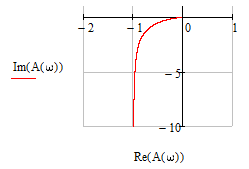 Рисунок 2.35 – График АФЧХ 2.7 Идеальное дифференцирующее звено Произведем замену 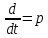 , чтобы перейти к операторному уравнению, получим: , чтобы перейти к операторному уравнению, получим: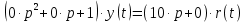 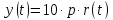 Передаточная функция: 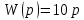 Весовая функция: 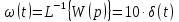 На рисунке 2.36 представлен график весовой функции. 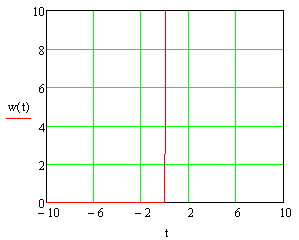 Рисунок 2.36 – График весовой функции Переходная характеристика: 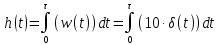 На рисунке 2.37 представлен график переходной характеристики. 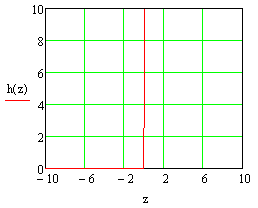 Рисунок 2.37 – График переходной характеристики Амплитудная частотная характеристика (АЧХ): 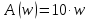 На графике 2.38 представлен график АЧХ. 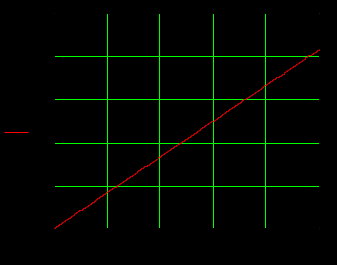 Рисунок 2.38 – График АЧХ Фазовая частотная характеристика (ФЧХ): 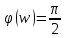 На графике 2.39 представлен график ФЧХ. 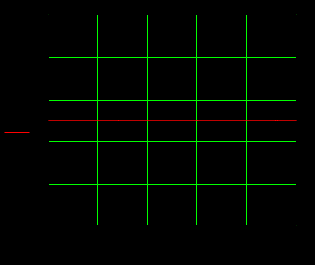 Рисунок 2.39 – График ФЧХ Логарифмическая амплитудная частотная характеристика (ЛАЧХ): 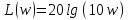 На рисунке 2.40 представлен график ЛАЧХ. 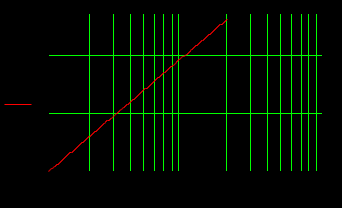 Рисунок 2.40 – График ЛАЧХ Амплитудно-фазовая частотная характеристика (АФЧХ): 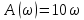 На рисунке 2.41 представлен график АФЧХ. 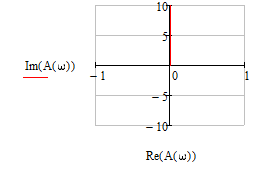 Рисунок 2.41 – График АФЧХ 2.8 Дифференцирующее звено с замедлением Произведем замену 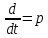 , чтобы перейти к операторному уравнению, получим: , чтобы перейти к операторному уравнению, получим: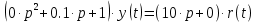 Передаточная функция: 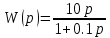 Весовая функция: 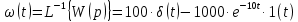 На рисунке 2.42 представлен график весовой характеристики. 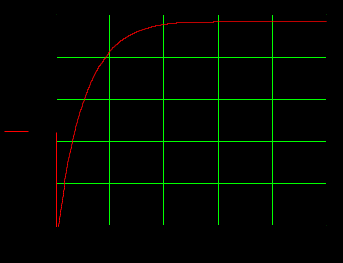 Рисунок 2.42 – График весовой характеристики Переходная характеристика: 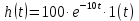 На рисунке 2.43 представлен график переходной характеристики. 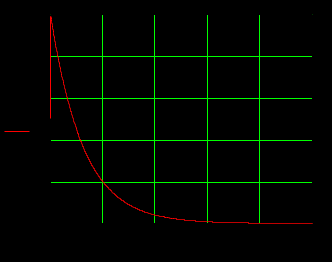 Рисунок 2.43 – График переходной характеристики Амплитудная частотная характеристика (АЧХ): 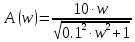 На рисунке 2.44 представлен график АЧХ. 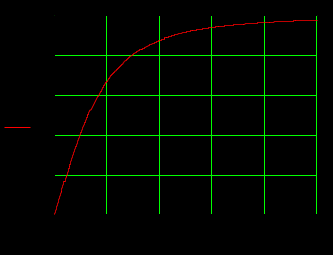 Рисунок 2.44 – График АЧХ Фазовая частотная характеристика (ФЧХ): 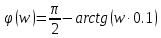 На рисунке 2.45 представлен график ФЧХ.  Рисунок 2.45 – График ФЧХ Логарифмическая амплитудно-частотная характеристика (ЛАЧХ): 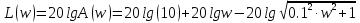 На рисунке 2.46 представлен график ЛАЧХ. 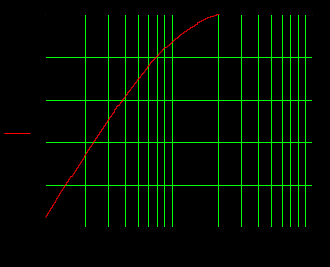 Рисунок 2.46 – График ЛАЧХ Амплитудно-фазовая частотная характеристика (АФЧХ): 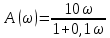 На рисунке 2.47 представлен график АФЧХ. 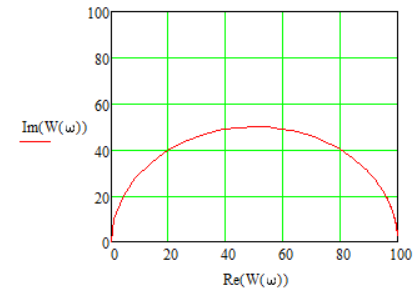 Рисунок 2.47 – График АФЧХ Для инерционных звеньев по логарифмическим частотным характеристикам определяем частоты сопряжения и среза. Инерционное 1-го порядка (апериодическое) звено: 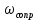 = 10 рад/с = 10 рад/с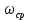 = 99,49 рад/с = 99,49 рад/сИнерционное 2-го порядка (апериодическое) звено: 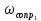 = 12,5 рад/с = 12,5 рад/с 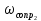 = 50 рад/с = 50 рад/с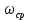 = 38 рад/с = 38 рад/сИнерционное 2-го порядка (колебательное) звено: 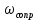 = 5 рад/с = 5 рад/с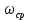 = 25 рад/с = 25 рад/сИдеально интегрирующее звено: 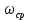 = 10 рад/с = 10 рад/сИдеально интегрирующее звено с замедлением: 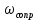 = 10 рад/с = 10 рад/с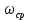 = 8 рад/с = 8 рад/сИдеально дифференцирующее звено: 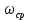 = 1 рад/с = 1 рад/сДифференцирующее звено с замедление: 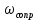 = 10 рад/с = 10 рад/с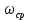 = 0,1 рад/с = 0,1 рад/сЗаключениеВ ходе данной лабораторной работы были изучены восемь основных типовых звеньев. Для каждого звена были найдены передаточная, весовая, переходные функции, амплитудно-частотная характеристика, фазовая частотная характеристика и логарифмическая амплитудно-частотная характеристика. По передаточной функции записаны операторные уравнения. Для инерционных звеньев по логарифмическим частотным характеристикам определены частоты сопряжения и среза. С помощью системы Mathcad были получены их графики. Также были составлены и решены дифференциальные уравнения. Томск 2019 |