Решение оптимизационной задачи с помощью надстройки EXCEL ЛР6 Пл. Отчет по дисциплине Информационные технологии в профессиональной деятельности Лабораторная работа 6. Тема Решение оптимизационной задачи с помощью надстройки excel Поиск решения
 Скачать 219.54 Kb. Скачать 219.54 Kb.
|
 Белова Ю.Н., МГУТУ, 2022 г. МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕХНОЛОГИЙ И УПРАВЛЕНИЯ ИМ. К.Г. РАЗУМОВСКОГО (ПЕРВЫЙ КАЗАЧИЙ УНИВЕРСИТЕТ) (ФГБОУ ВО МГУТУ им. К.Г.РАЗУМОВСКОГО (ПКУ))   Институт: Системной автоматизации, информационных технологий и предпринимательства  09.03.01 «Информатика и вычислительная техника» Кафедра: Информационные системы и технологии Направление подготовки – ОТЧЕТ ПО ДИСЦИПЛИНЕ «Информационные технологии в профессиональной деятельности» Лабораторная работа №6. Тема: «Решение оптимизационной задачи с помощью надстройки EXCEL «Поиск решения»»  Вариант № 17 Вариант № 17
Москва, 2022 г. Экономическая постановка задачи Для поддержания нормальной жизнедеятельности человеку ежедневно необходимо потреблять не менее 118 г белков,56 г. жиров, 500 г. Углеводов, 8 г. Минеральных солей. Количество питательных веществ, содержащихся в 1 кг каждого вида потребляемых продуктов, а также цена за 1 кг каждого из этих продуктов приведены в следующей таблице:
Составить дневной рацион, содержащий не менее минимальной суточной нормы потребности человека в необходимых питательных веществах при минимальной общей стоимости потребляемых продуктов. Математическая постановка задачи. Обозначим неизвестные переменные: x1 – количество потребляемого за сутки мяса x2 – количество потребляемого за сутки рыбы х3 – количество потребляемого за сутки молока х4 – количество потребляемого за сутки масла х5 – количество потребляемого за сутки сыра х6 – количество потребляемого за сутки крупы х7 – количество потребляемого за сутки картофеля Требуется найти наилучшие значения x1-х7 Наилучшими для данной задачи являются такие значения, которые минимизируют общую стоимость потребляемых продуктов. Целевая функция: Z= 18*x1 +10*х2+2,8*х3+34*х4+29*х5+5*х6+1*х7 → min Формируем ограничения: Поскольку х1-7 выражают количество потребляемых продуктов, то они не могут быть отрицательны, т.е. х1 ≥0, х2 ≥0, х3 ≥0, х4≥0, х5 ≥0, х6≥0, х7≥0 Ограничения на минимальную суточную норму могут быть записаны следующим образом: Х1*180+Х2*190+ Х3*30+ Х4*10+ Х5*260+ Х6*130+Х7*21≥118 Х1*20+Х2*3+ Х3*40+ Х4*865+ Х5*310+ Х6*30+Х7*2≥56 Х1*0+Х2*0+ Х3*50+ Х4*6+ Х5*20+ Х6*650+Х7*200≥500 Х1*9+Х2*10+ Х3*7+ Х4*10+ Х5*60+ Х6*20+Х7*10≥8 Таким образом, задача состоит в том, чтобы найти значения Х, удовлетворяющим условиям: Х1-7≥0 Х1*180+Х2*190+ Х3*30+ Х4*10+ Х5*260+ Х6*130+Х7*21≥118 Х1*20+Х2*3+ Х3*40+ Х4*865+ Х5*310+ Х6*30+Х7*2≥56 Х1*0+Х2*0+ Х3*50+ Х4*6+ Х5*20+ Х6*650+Х7*200≥500 Х1*9+Х2*10+ Х3*7+ Х4*10+ Х5*60+ Х6*20+Х7*10≥8 И минимизирующие функцию S=18 x1 +10 х2+2,8 х3+34 х4+29 х5+5 х6+1* х7 Формирование шаблона решения задачи в EXCEL 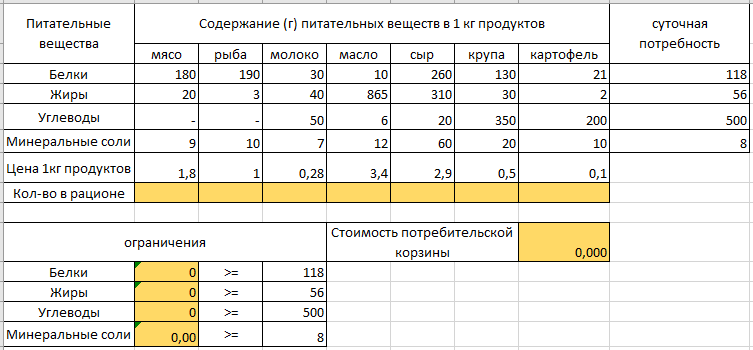 Ячейки, в которых должен появиться ответ, закрашены желтым цветом. Шаблон решения с указанием формул в расчетных ячейках. 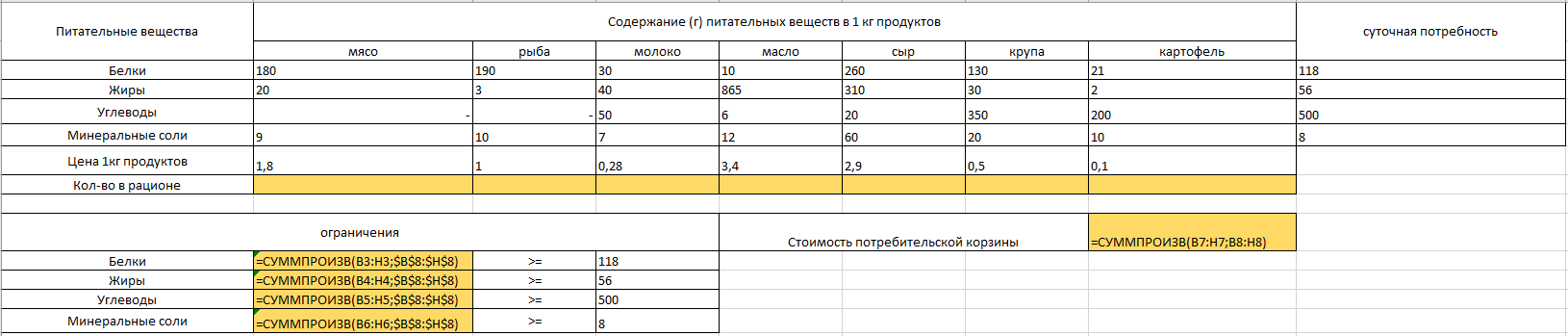 Настройка и запуск поиска решения Окно «Поиск решения» с необходимыми настройками 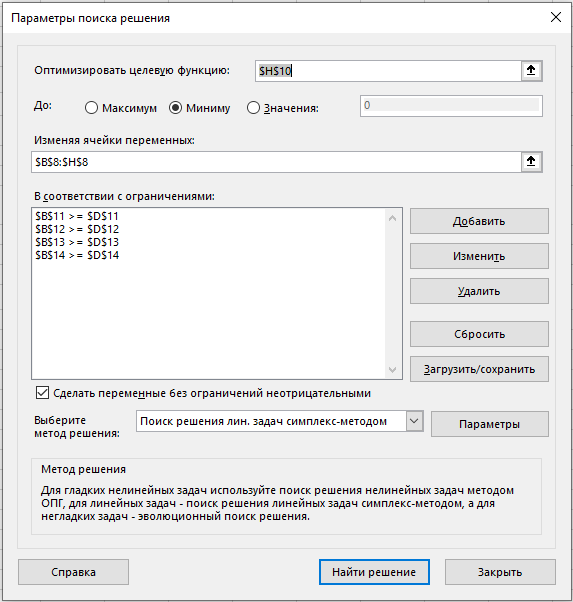 Результаты решения задачи оптимизации 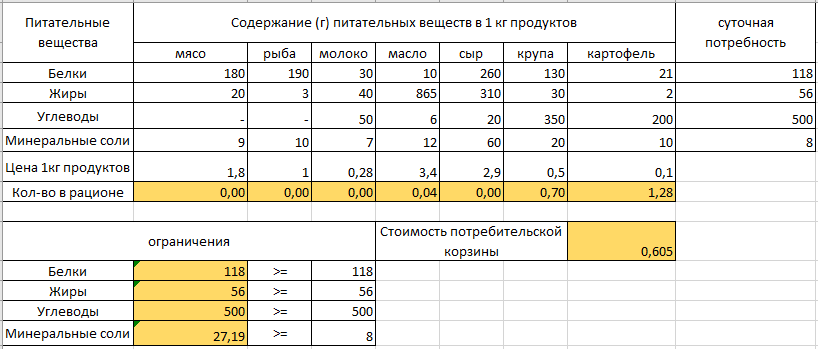 Отчет о результатах (создается через Поиск решения) 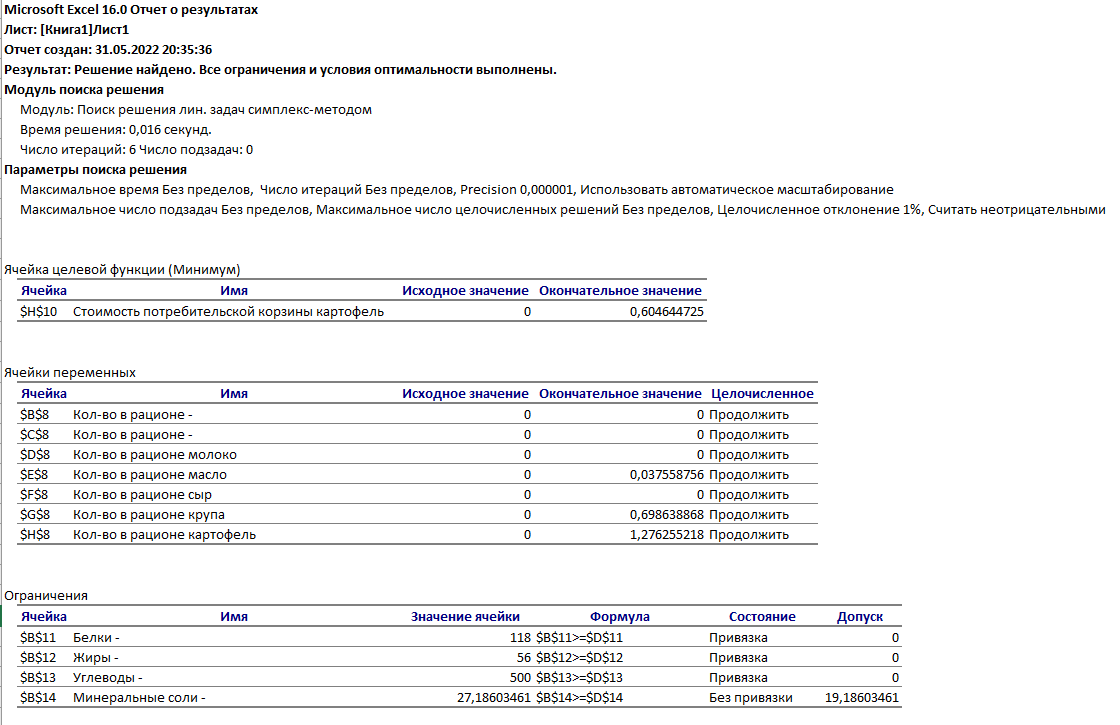 Вывод по решению задачи оптимизации. Задача оптимизации о нахождении оптимального плана питания, дающего минимальные затраты на продукцию, решена симплекс-методом с помощью надстройки MS Excel «Поиск решения». | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
