графы дискретная математика. инд раб графы 2. Отчет по индивидуальной работе 2 по дисциплине Дискретная математика
 Скачать 470.29 Kb. Скачать 470.29 Kb.
|
|
МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Хакасский государственный университет им. Н.Ф. Катанова» (ХГУ им. Н.Ф. Катанова) Инженерно-технологический институт (ИТИ) Кафедра информационных технологий и систем (ИТиС) ОТЧЕТ ПО ИНДИВИДУАЛЬНОЙ РАБОТЕ №2 по дисциплине «Дискретная математика» Выполнил: студент группы 220 Доржу А.Ш Проверил: Молчанова. Е.А Абакан 2021 ВАРИАНТ – 3 Задание Найти компоненты сильной связности 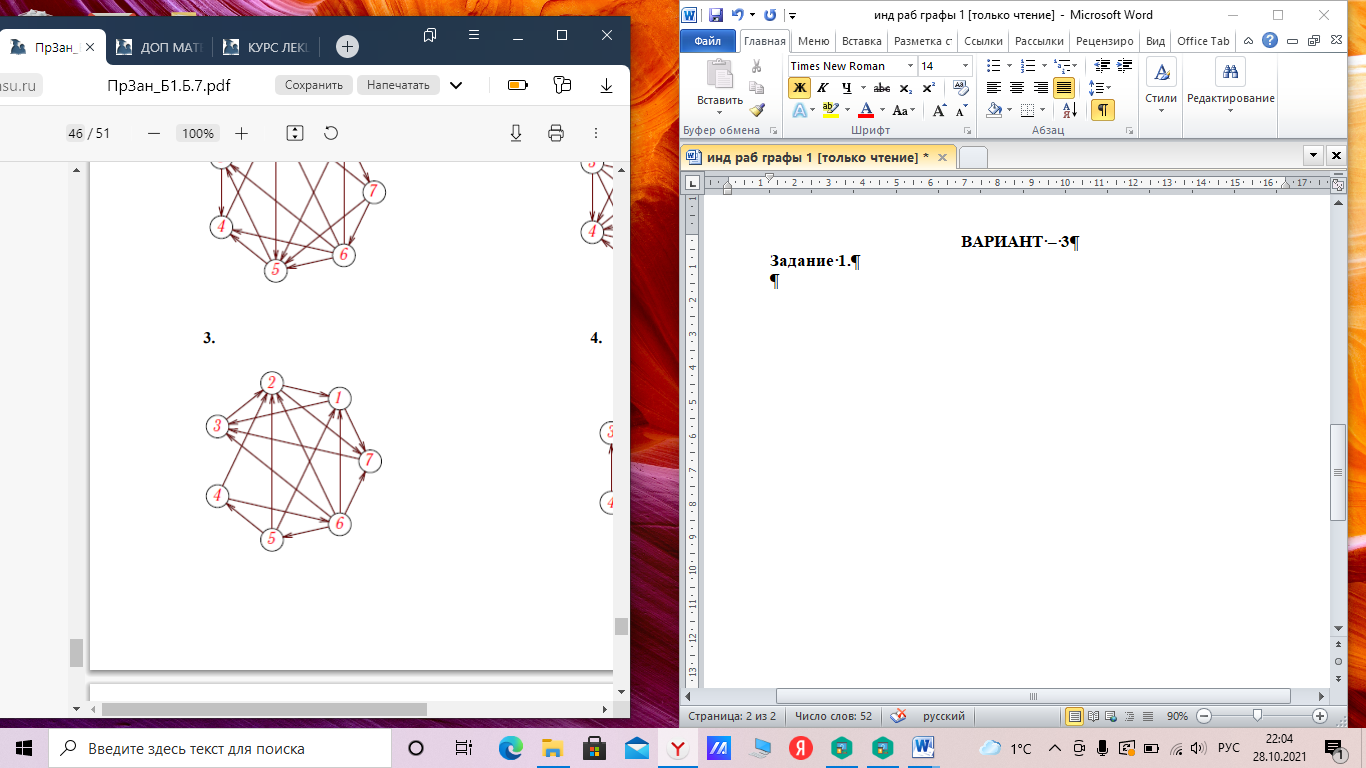 Построим матрицу смежности. Так как в данном графе количество вершин N=7, матрица смежности будет иметь размерность 7×7. A(D) = 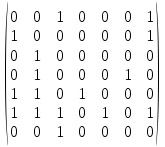 Найдем матрицу достижимости для данного орграфа по T(D)= [E+A+A 2 +A 3 +… A N-1 ] [A(D)]2 =  [A(D)]3 = 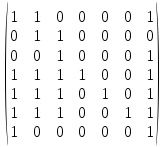 [A(D)]4 = 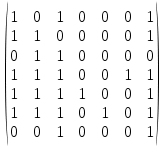 [A(D)]5 = 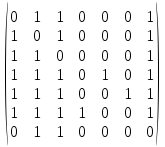 [A(D)]6 = 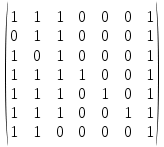 Найдем T(D) , 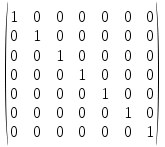 + +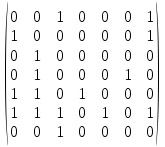 + + + ++ 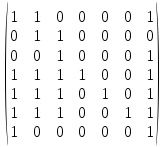 + +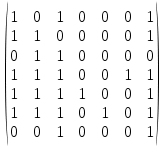 + +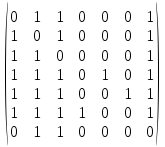 + ++ 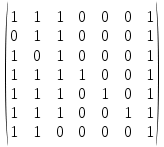 = = 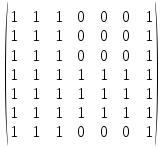 Таким образом, матрица сильной связности, полученная по S(D)=T(D)&TT (D), где TT -транспонированная матрица, &-поэлементное умножение, будет следующей: S(D) = 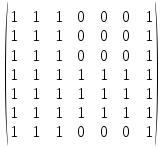 & &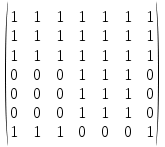 Присваиваем P=1 S1=S(D) составляем множество вершин первой компоненты сильной связности D1: это те вершины, которым соответствуют единицы в первой строке матрицы S(D). Таким образом, первая компонента сильной связности состоит из вершин V1= {v1, v2, v3, v7}. Составляем матрицу смежности для компоненты сильной связности D1 исходного графа D − в ее качестве возьмем подматрицу матрицы A(D), состоящую из элементов матрицы A, находящихся на пересечении строк и столбцов, соответствующих вершинам из V1: A(D1  Вычеркиваем из матрицы S1(D) строку и столбец, соответствующие вершине V1, чтобы получить матрицу S2(D) S2 (D) =  Присваиваем P=2. Множество вершин второй компоненты связности составят те вершины, которым соответствуют единицы в первой строке матрицы S2(D), то есть V2= {v4, v5, v6}. Составляем матрицу смежности для компоненты сильной связности D2 исходного графа D − в ее качестве возьмем подматрицу матрицы A(D), состоящую из элементов матрицы A, находящихся на пересечении строк и столбцов, соответствующих вершинам из V2: A(D2  Вычеркиваем из матрицы S2(D) строки и столбцы, соответствующие вершинам из V2, чтобы получить матрицу S3(D), которая состоит из пустого множества: S3(D)= ( ) присваиваем P=3. Таким образом, третья компонента сильной связности исходного графа отсутствует. Таким образом, выделены 2 компоненты сильной связности ориентированного графа D: 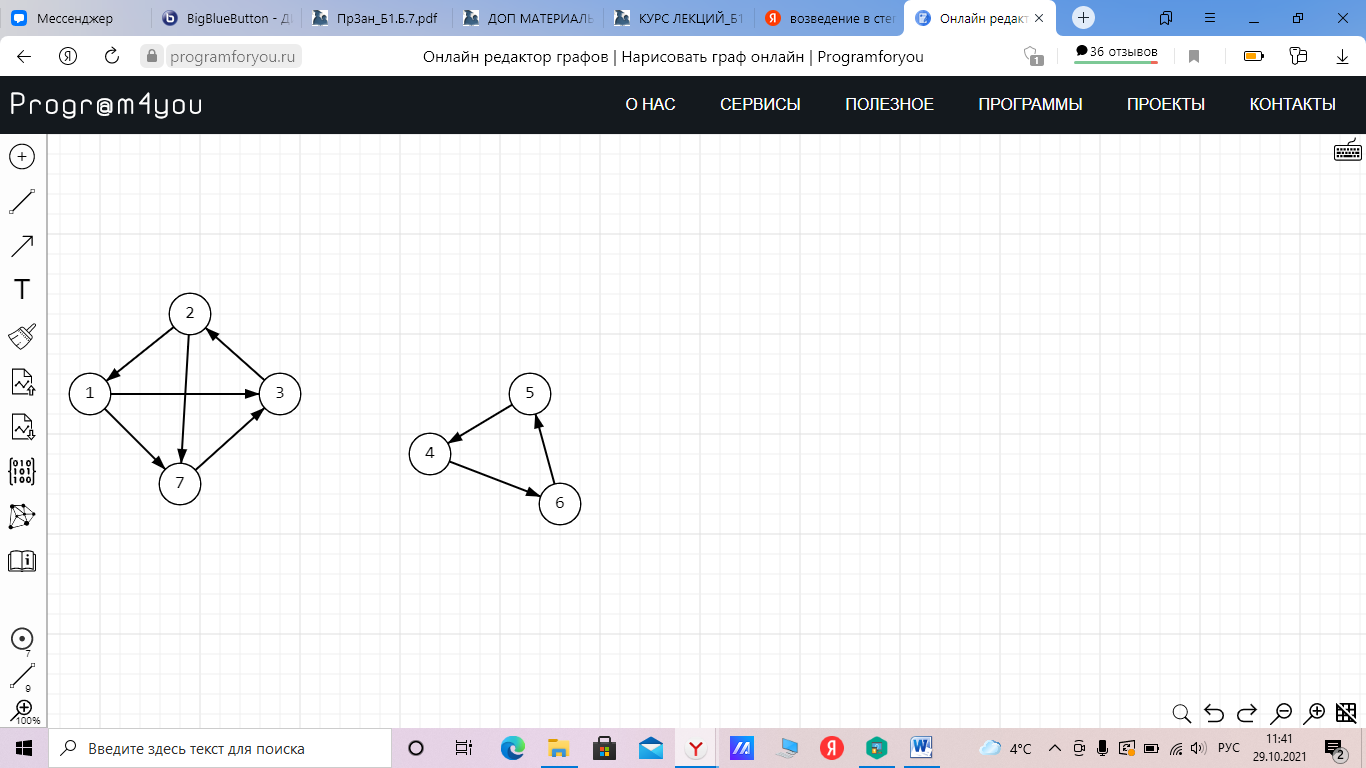 |
