Отчет по индивидуальному домашнему заданию 3 Тема Основы фрактальной геометрии Вариант 8 Студент группы 1104 Кадол Г. Ю. Преподаватель Рассадина А. А
 Скачать 351.61 Kb. Скачать 351.61 Kb.
|
|
МИНОБРНАУКИ РОССИИ "САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ "ЛЭТИ"" ИМ. В.И.УЛЬЯНОВА(ЛЕНИНА) Кафедра МИТ ОТЧЕТ По индивидуальному домашнему заданию №3 Тема: Основы фрактальной геометрии Вариант 8 Студент группы 1104: Кадол Г.Ю. Преподаватель: Рассадина А.А. Санкт-Петербург 2022 Задания №1: Рассчитать фрактальная размерность математических фракталов в соответствии с данными по индивидуальному заданию и сделать выводы. Дано: Кривая дракона Решение: Придумал ее физик Хейтуэй, Бэнксом, Хартер. Описана в 1967 году Гарднером в журнале «Scientific American». Для построения классического фракатал Дракон Хартера возьмем отрезок, на втором шаге повернем его на 90 вокруг одной из вершин и добавим новый полученный отрезок к исходному. Получим уголок из двух отрезков. Повторим описанную процедуру. Повернем уголок на 90о вокруг вершины и добавим полученную ломаную к исходной. Повторяя названные действия и уменьшая ломаные, будем получать изображение, напоминающие фигуру дракона. Получение кривой дракона с помощью геометрического построения Бенкс придумал способ, позволяющий получать кривые дракона с помощью геометрического построения. Сначала берется отрезок единичной длины. Затем он заменяется на два отрезка, образующих боковые стороны равнобедренного прямоугольного треугольника, для которых исходный отрезок является гипотенузой. В результате отрезок как бы прогибается под прямым углом. Направление прогиба чередуется. Первый отрезок прогибается вправо (по ходу движения слева направо), второй - влево, третий - опять вправо и т.д. Таким образом, после каждого шага число имеющихся отрезков удваивается, а длина каждого соответственно уменьшается в 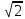 раз. раз.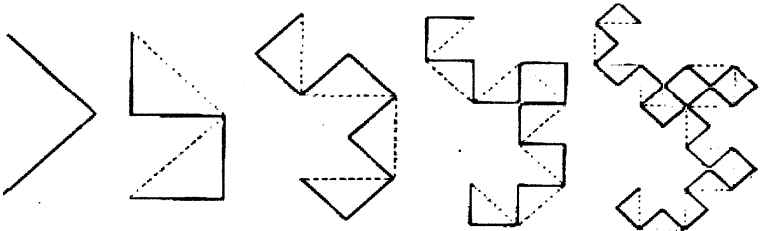 Фрактал может быть записан как L-система с параметрами: • угол равен 90° • начальная строка — FX • правила преобразования строк: • X X+YF+ • Y -FX-Y Фрактальная размерность кривой Дракона. Можно увидеть «повторения» в кривой дракона. Очевидно, что рисунок повторяется по той же схеме, с наклоном в 45 ° и коэффициентом сжатия равном корню из двух. Таким образом, точки сгиба образуют логарифмическую спираль. 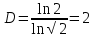  Рис.2. Получение кривой Дракона. Вывод: Кривая дракона является примером самоподобной кривой. Очень легка в построении. Таким образом, после каждого шага число имеющихся отрезков удваивается, а длина каждого соответственно уменьшается в раз. Поэтому фрактальная размерность образующейся в результате (после бесконечного числа шагов) кривой равна 2, т.е. кривая заметает собой конечную площадь. |
