ТЕОРИЯ ИЗМЕРЕНИЙ: ответы на вопросы. ТИ экз. Отчет по курсу теория измерений голубева М. К студентка группы 3334 Преподаватель Бельский А. М
 Скачать 3.25 Mb. Скачать 3.25 Mb.
|
 Казанский национальный исследовательский технический университет имени Казанский национальный исследовательский технический университет имени А. Н. Туполева – КАИ Институт автоматики и электронного приборостроения Кафедра электронного приборостроения и менеджмента качества ОТЧЕТ ПО КУРСУ ТЕОРИЯ ИЗМЕРЕНИЙ Выполнила: Голубева М.К.. студентка группы 3334 Преподаватель: Бельский А.М. Казань 2018 1. Основы математической статистики Математическая статистика – это раздел прикладной математики, в которой с помощью наблюдений и экспериментов стараются выяснить и сформировать законы и характеристики случайных величин. Математическая статистика, опираясь на теорию вероятности, помогает обрабатывать статистические данные во многих областях деятельности человека. Основные задачи математической статистики: 1.Создание методов сбора и группировки данных, полученных в результате наблюдений за случайными процессами. 2. Разработка методов анализа полученных статистических данных. 3. Получение выводов по данным наблюдений Для анализа собранных данных нам необходимо их оценить и выразить вероятность события. Также в анализ входят функции распределения вероятностей или плотности вероятностей, оценка параметров известного распределения, оценка связей между случайными величинами. Основные понятия математической статистики – генеральная совокупность и выборка. Генеральная совокупность – это все множество исследования объектов вида, над которыми проводятся наблюдения. Она может быть бесконечной и конечной. Выборкой (выборочной совокупностью)называется совокупность случайно отобранных объектов из генеральной совокупности, которая необходима для исследования. Чтобы отчетливо отражать свойства генеральной совокупности, выборка должна быть представительной или репрезентативной. Выборочная совокупность бывает повторной, когда отобранный объект возвращают в генеральную совокупность, и бесповторной, когда объект не возвращают обратно. Существует несколько способов получения выборки:простой, типический, серийный, механический. 1) Простой отбор – случайное извлечение объектов из генеральной совокупности с возвратом или без возврата. 2) Типический отбор, когда объекты отбираются не из всей генеральной совокупности, а из ее «типической» части. 3) Серийный отбор – объекты отбираются из генеральной совокупности не по одному, а сериями. 4)Механический отбор - генеральная совокупность «механически» делится на столько частей, сколько объектов должно войти в выборку и из каждой части выбирается один объект. Для обработки данных наблюдаемые значения случайной величины располагают в порядке возрастания, то есть используют операциюранжирования: 1.Размах варьирования R= 2.Мода ( 3.Медиана ( Когда изучаемая случайная величина Х является непрерывной или число значений её велико, то составляют интервальный статистический ряд. Эмпирической функцией (функцией распределения выборки) называется функция F*(x), определяющая для каждого значения х частость события где n – число выборки , nx – число наблюдений, меньших x Эмпирическая функция F*(х) является оценкой интегральной функции F(x) в теории вероятностей. Функция F*(х) обладает теми же свойствами, что и функция F(x): 1. 2. F*(x) – неубывающая функция 3. Для интегральной функции распределения F(x): Чтобы изобразить статистическое распределение графически, используют полигона и гистограммы. Полигоном частот называют ломаную, отрезки которой соединяют точки с координатами (хi;ni). Полигон служит для изображения дискретного статистического ряда. Полигон частостей является аналогом многоугольника распределения дискретной случайной величины в теории вероятностей. 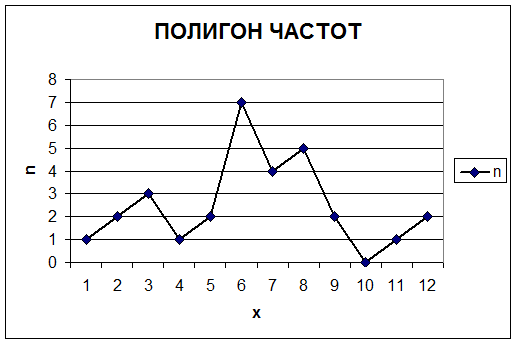 Гистограммой частот (частостей) называют ступенчатую фигуру, состоящую из прямоугольников, основания которых расположены на оси Ох и длины их равны длинам частичных интервалов (h), а высоты равны отношению: 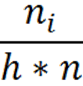 - для гистограммы - для гистограммычастостей. Гистограмма является графическим изображением интервального ряда. Площадь гистограммы частот равна n, а гистограммы частостей равна 1.  Можно построить полигон для интервального ряда, если преобразовать его в дискретный ряд. В этом случае интервалы заменяют их серединными значениями и ставят в соответствие интервальные частоты (частости). 2. Однократные измерения Однократные измерения – совокупность операций, при которых необходимо воспроизвести единицу физической величины, сравнить с ней измеряемое значение, зафиксировать результаты сравнения и оценить погрешность измерения. Однократные измерения можно считать частным случаем многократных измерений, потому что: 1) При совершении однократных измерений применяются средства измерений с метрологическими характеристиками, определенными при совершении многократных измерений; 2) Представление результатов измерений требует учета всех погрешностей и доверительной вероятности. Однократные измерения требуют меньше времени, являются менее трудоемкими и более удобными для практического использования. Например, при совершении торговых операций. Необходимо отметить, что однократные измерения не проще многократных, несмотря на меньшее количество измерений и отсутствие применений вероятностных статистических методов при обработке данных. Когда проводят однократное измерение, за результат принимают полученное значение величины. Из-за того, что по одному измерению невозможно определить погрешность результата, нужно использовать информацию, которую мы получаем априори: важно правильно выбрать средство измерений для данных условий и определить диапазоны измерений. Например, если мы собираемся измерять массу каких-либо веществ, необходимо познакомиться с весоизмерительным оборудованием и провести предварительный анализ источников погрешностей. Правильность оценивания погрешностей результата измерений зависит от полноты учета всех факторов, влияющих на результат измерений, и от метода нахождения этих погрешностей. Конечно, в реальной жизни мы не можем учесть все возможные факторы, но всегда требуется дать наиболее точный результат. На совершение однократных измерений существует свой нормативный документ Госстандарта России – МИ 1552-86 «Государственная система обеспечения единства измерений. Измерения прямые однократные. Оценивание погрешностей результатов измерений». МИ 1552-86 распространяется на нормативную, конструкторскую, технологическую и другую документацию, регламентирующую требования к выполнению измерений, и устанавливает методы оценивания погрешностей результатов прямых однократных измерений. Измерения проводятся при нормальных условиях (температуры, давления и т.д.). Дополнительные погрешности, зависящие от условий измерения, в этом случае равны нулю. При расширении диапазона измерений или при условиях измерений, отличающихся от нормальных, появляются дополнительные погрешности, которые приходится учитывать. 3. Многократные наблюдения Если необходима большая уверенность в получаемом результате, то проводятся многократные измерения. Если говорить коротко, то измеряют величину одного и того же размера, результат которого состоит из множества однократных измерений. Все проходит в одинаковых условиях с одними и теми же средствами измерения. Прежде чем приступить к обобщению результатов измерений, определяют, нет ли в полученных результатах грубых погрешностей. За результат многократного измерения обычно принимают среднее арифметическое значение из результатов однократных измерений, входящих в ряд. Такие измерения характерны при выполнении метрологических работ, а также находят широкое применение в научных исследованиях. Важной чертой многократных измерений является получение и использование большого объема измерительной информации. Применение многократных измерений позволяет повысить точность измерения до определенного предела, но недостаток полученной информации не позволяет получить точное значение поправок, значений составляющих погрешностей и т.п. В связи с этим устанавливают необходимое число измерений, которое позволяет получить результат измерений, в котором случайная погрешность пренебрежимо мала по сравнению с неисключенной систематической погрешностью. Лабораторная работа №1 Оценка результатов прямых равноточных многократных измерений Согласно ГОСТ 8.207-76 обработка результатов наблюдений производится в последовательности: 1. Исключаются известные систематические погрешности из результатов наблюдений. 2. Определяют границы неисключенной систематической погрешности (остатка) результата измерений. 3. Вычисляется среднее арифметическое исправленных результатов наблюдений, которое принимается за результат измерения. Вычисляется оценка СКО результатов наблюдений. 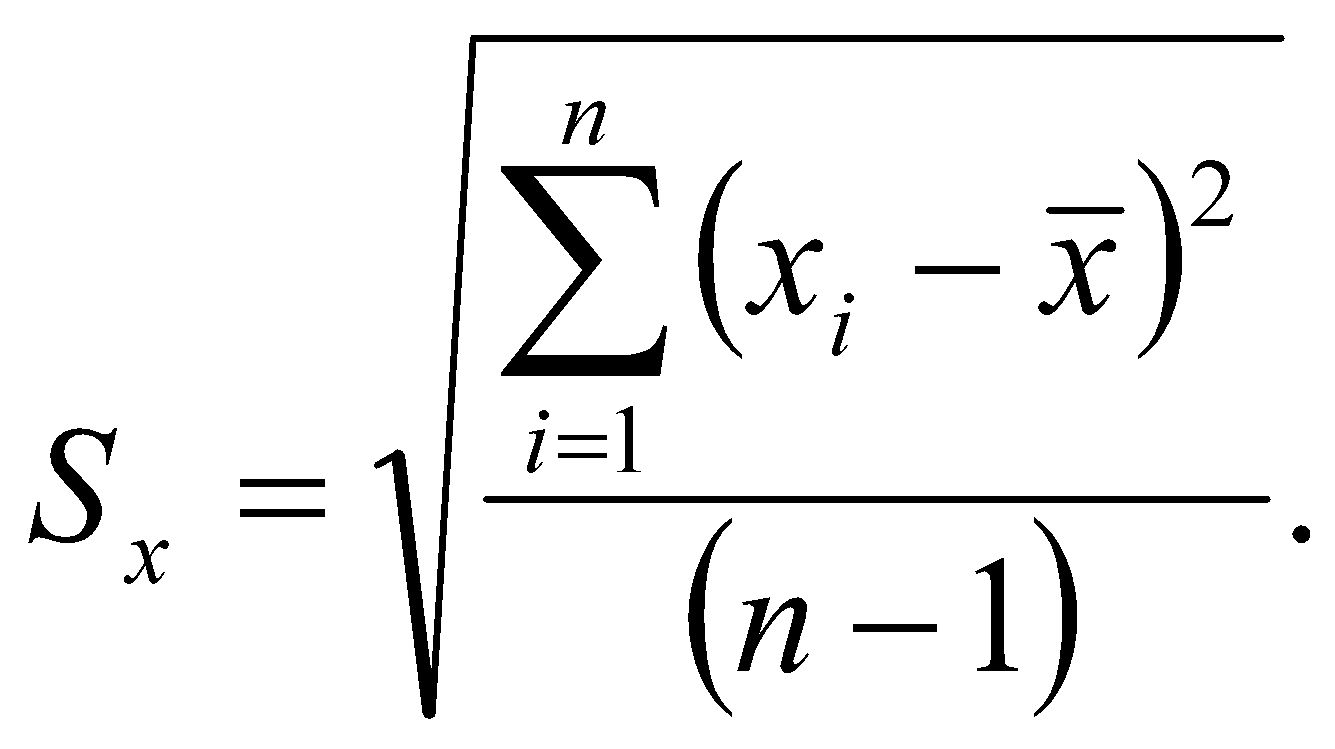 Проверяется наличие в группе наблюдений грубых погрешностей. Если они есть, то их исключают из группы и вновь повторяют вычисление 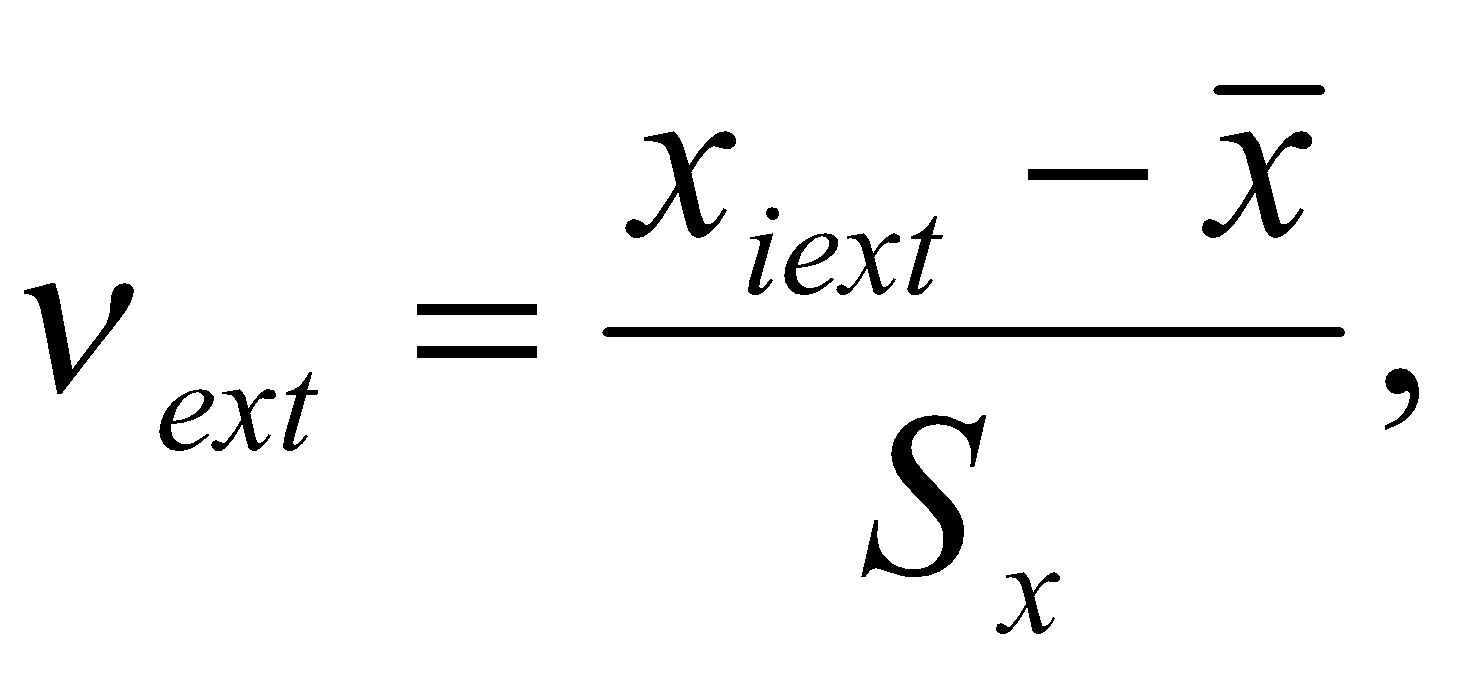 где Полученные результаты νext сравним с приложением 1. 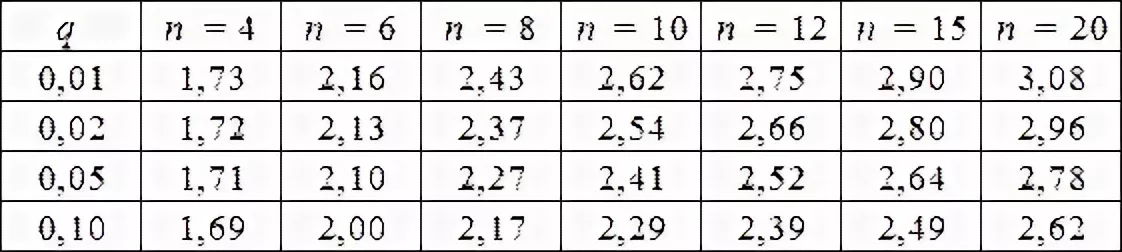 6. Вычисляют оценку СКО среднего арифметического. 7. Проверяют гипотезу о принадлежности результатов наблюдений к нормальному закону распределения. Проверку нормальности, согласно ГОСТ 11.006–74, при n >50, проводят по критериям Пирсона или Мизеса–Смирнова. При 15 < n < 50 используют двойной составной q–критерий. 8. Вычисляют доверительные границы случайной погрешности(случайной составляющей погрешности).  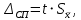 где t - коэффициент Стьюдента. 9. Вычисляют доверительные границы погрешностей результата измере-ния. Доверительную вероятность 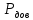 принимают такой же, что при вычислении границ принимают такой же, что при вычислении границ 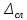 . .Результаты измерений:
Систематические погрешности – 0,92 и 1,15. n = 8, 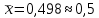 , , 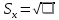 , Δсп = 3,71*0,097 = 0,36 (Pдов = 0,99, t = 3,71). , Δсп = 3,71*0,097 = 0,36 (Pдов = 0,99, t = 3,71).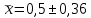 Лабораторная работа№2 Определение класса точности осциллографа Класс точности – обобщенная характеристика средств измерений, определяемая пределами допускаемых основных и дополнительных погрешностей, а также рядом других свойств, влияющих на точность осуществляемых с их помощью измерений. Имеется два подхода к нормированию погрешностей средств измерений. 1.Единые правила установления пределов допускаемых погрешностей показаний по классам точности регламентирует ГОСТ 8.401-80. Под классом точности СИ понимают их обобщенные характеристики, определяемые пределами допускаемой основной и дополнительной погрешности. При этом нет деления на погрешность систематическую и случайную. ГОСТ 8.401-80 не устанавливает классы точности СИ, для которых предусмотрены нормы отдельно для систематической и случайной составляющих погрешностей, а так же если необходимо их учитывать динамические характеристики. Классы точности устанавливаются в тех случаях, когда погрешности СИ могут быть выражены числом или сравнительно простой формулой. Второй метод сформулирован ГОСТ 8.009-84. “ Нормирование и использование метрологических характеристик средств измерений” Данный стандарт устанавливает комплекс метрологических характеристик, которые должны быть известны при выпуске СИ.  Результаты измерений:
n = 8, 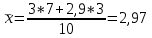 , , 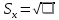 , Δсп = 3,3*0,48 = 0,159. , Δсп = 3,3*0,48 = 0,159.Δ = 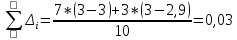 K = 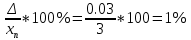 Выполнив вычисления можно сделать, что осциллограф относится к 6 классу точности.. 4. Косвенные измерения Косвенными называют такие измерения, при которых числовое значение измеряемой величины определяется по известной функциональной зависимости через другие величины, которые можно прямо измерить. При косвенных измерениях числовое значение измеряемой величины получают с участием оператора на основе прямых измерений – решением одного уравнения. К косвенным измерениям прибегают в тех случаях, когда неудобно или невозможно осуществить автоматическое вычисление известной зависимости между одной или несколькими входными величинами и измеряемой величиной. Например, мощность в цепях постоянного тока определяет оператор, умножая напряжение на ток, измеренные прямым измерением с помощью амперметра и вольтметра. В этом случае искомое значение величины находят на основе измерения других величин в соответствии с зависимостью Результат находят из решения уравнения, выражающего эту зависимость: Q = f(X, Y, Z, ... , W). где Q – измеряемая величина; X, Y, Z,..., W – величины, размер которых определяется из прямых измерений. Например, требуется измерить удельное электрическое сопротивление некоторого материала. Так как приборов для прямых измерений удельного сопротивления нет, его можно измерить только косвенно. Для этого воспользуемся уравнением где р – удельное сопротивление; R – электрическое сопротивление; S – площадь поперечного сечения; L – длина образца. Если измерить длину L, площадь поперечного сечения S и электрическое сопротивление R, то можно вычислить и его удельное сопротивление. Косвенные измерения достаточно часто встречаются в метрологии, где ими пользуются при воспроизведении единиц. Такие измерения позволяют получать более точный результат, чем прямые. Особенно велика роль косвенных измерений в естественных науках, когда реализация прямых измерений при изучении явлений затруднительна. Например, явления, изучаемые в астрономии, молекулярной и атомной физике и т. д. Примеры косвенных измерений: определение эффективной мощности двигателя при его испытании на основании прямых измерений крутящего момента и частоты вращения вала двигателя; определение площади фигур или объема тел по прямым измерениям их геометрических размеров. Методика обработки результатов косвенных измерений приведена в МИ2083-90 «ГСИ. Измерения косвенные. Определение результатов измерений и оценивание их погрешностей». Совместные и совокупные измерения Эти измерения характеризуются тем, что значения искомых величин находят из решения системы уравнений, которые связывают искомые величины с некоторыми другими, получаемыми в результате эксперимента посредством прямых или косвенных измерений. Если измеряемые величины - одноименные, измерения называются совокупными, если неодноименные – совместными. Целью таких измерений обычно является установление функциональной зависимости между измеряемыми величинами. Это возможно путем замены экспериментальных данных значениями некоторой теоретической функции. Если замена справедлива для всех значений аргумента в заданном интервале, то заменяющую функцию называют аппроксимирующей. Если замена справедлива только для некоторых, дискретных значений аргумента –функцию называют интерполирующей. Очевидно, что подобные задачи должны решаться в два этапа: ∙ выбор структуры предполагаемой зависимости, т. е. выбор вида математической модели (линейная, полиномиальная, экспоненциальная и т. п.); ∙ вычисление параметров (коэффициентов) этой модели. В связи с этим, при выполнении совместных измерений, во-первых, возникает задача выбора аппроксимирующее зависимости Одним из возможных вариантов решения подобных задач это применение метода наименьших квадратов (МНК). В этом методе оценки параметров выбранной модели определяют из условия, что сумма квадратов отклонений расчетных значений аппроксимирующей функции от экспериментальных значений должна быть минимальна. При этом полагают, что результаты измерений ∙ значения аргументов ∙ систематические погрешности из При выполнении этих условий МНК дает несмещенные оценки параметров модели, имеющие минимальные дисперсии. Пусть искомые значения величин 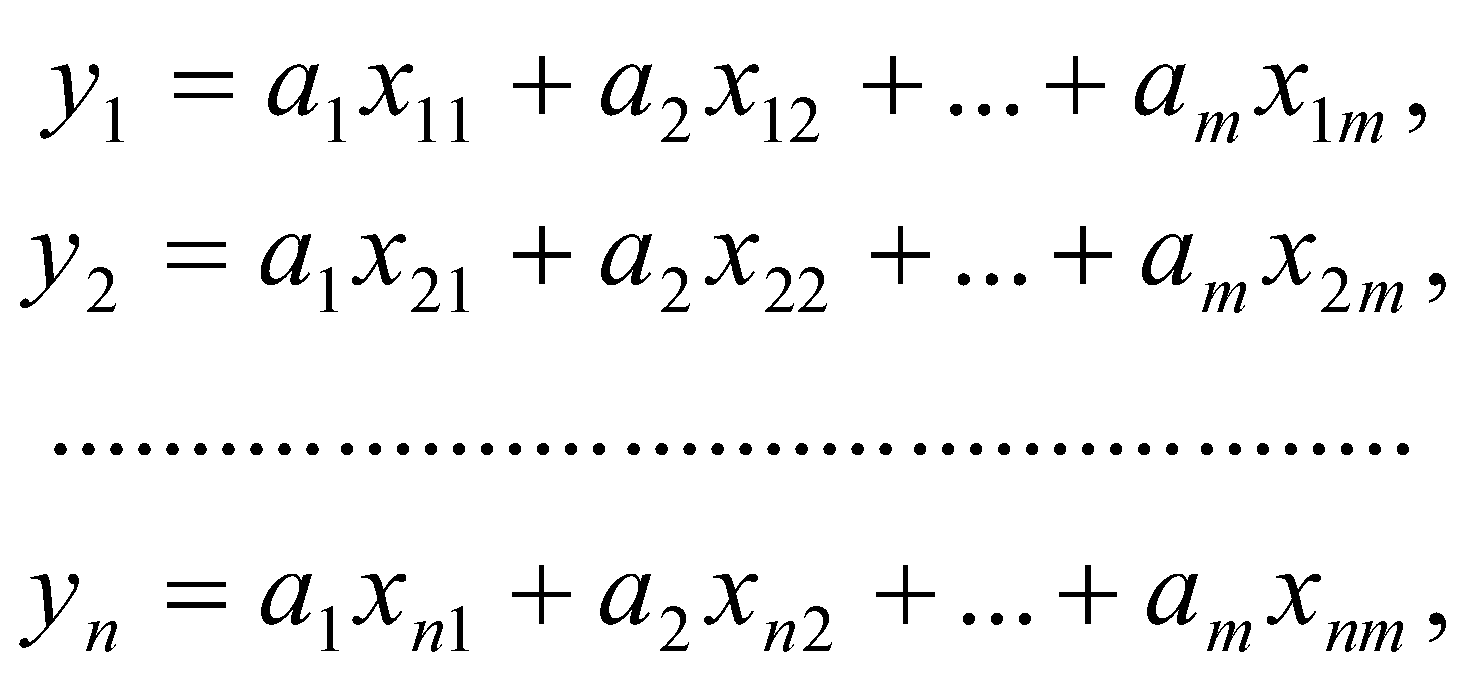 (35) (35)здесь Систему уравнений (35) перепишем в виде 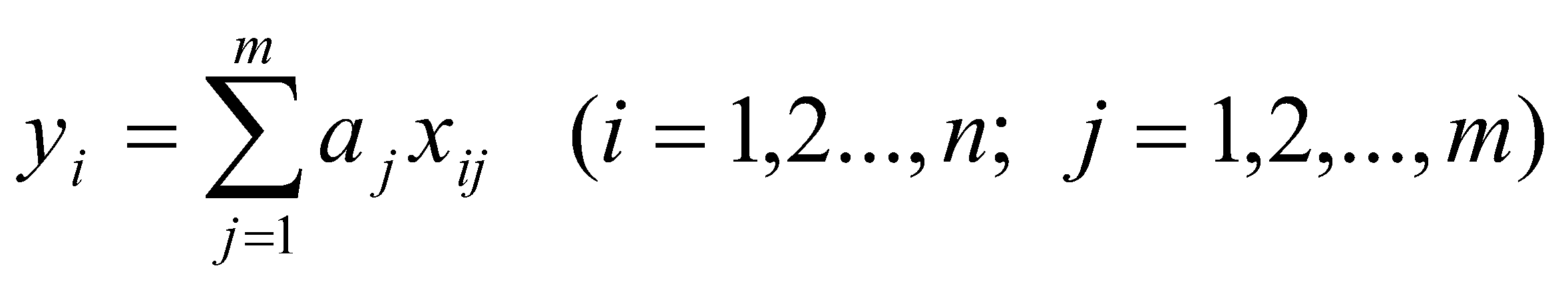 (36) (36)Так как 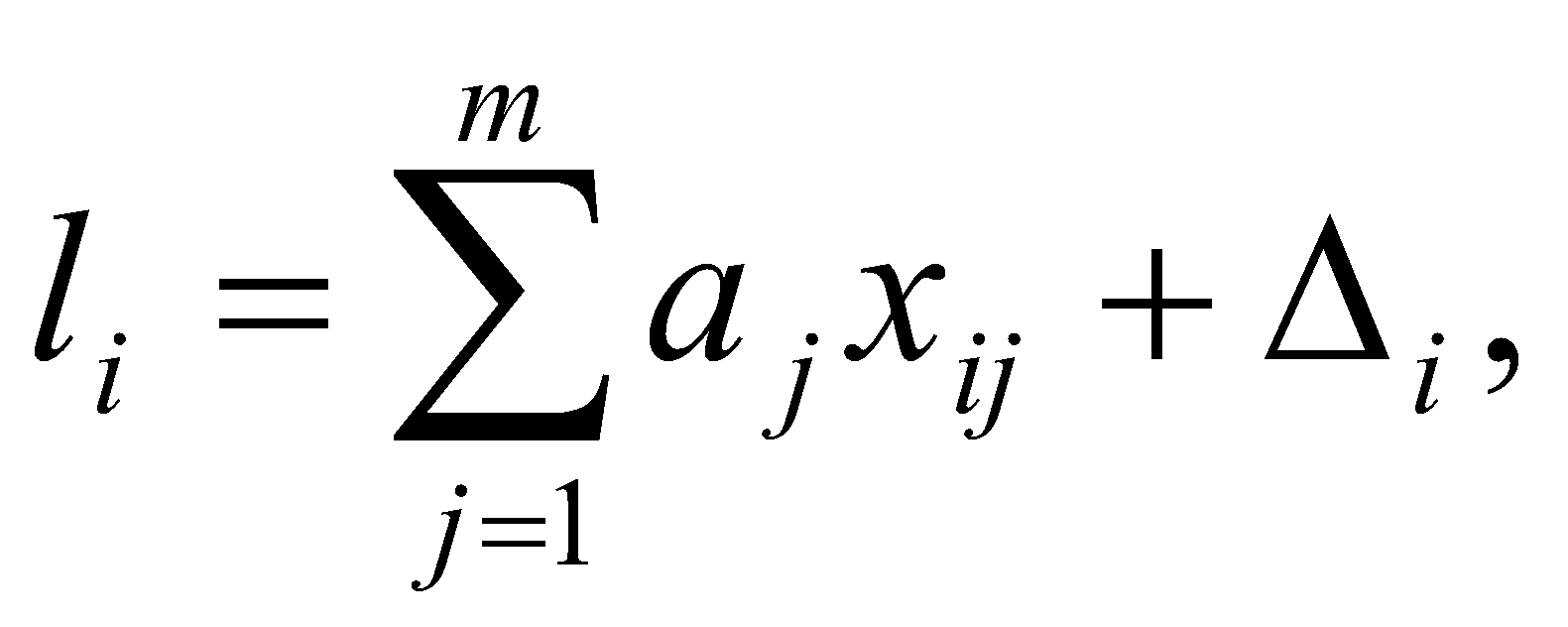 (37) (37)или 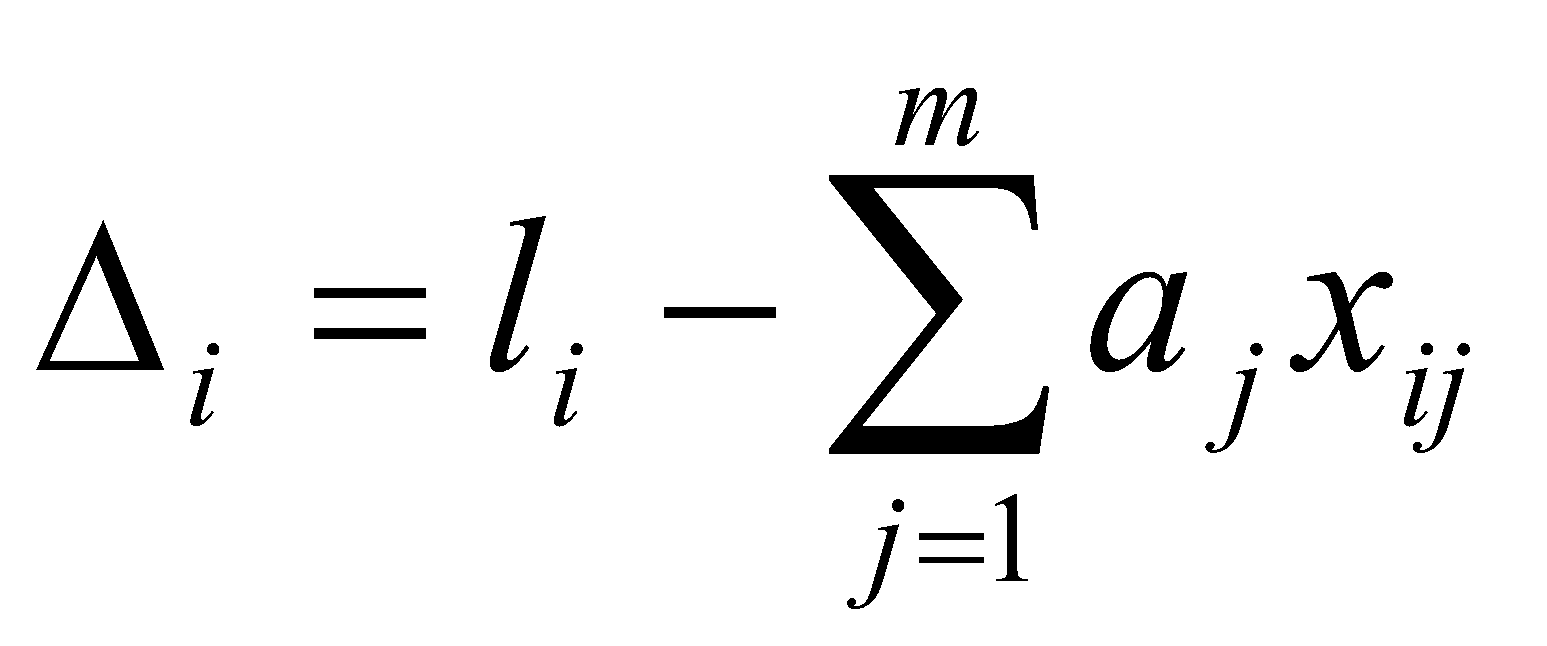 В соответствии с МНК наилучшие оценки для или 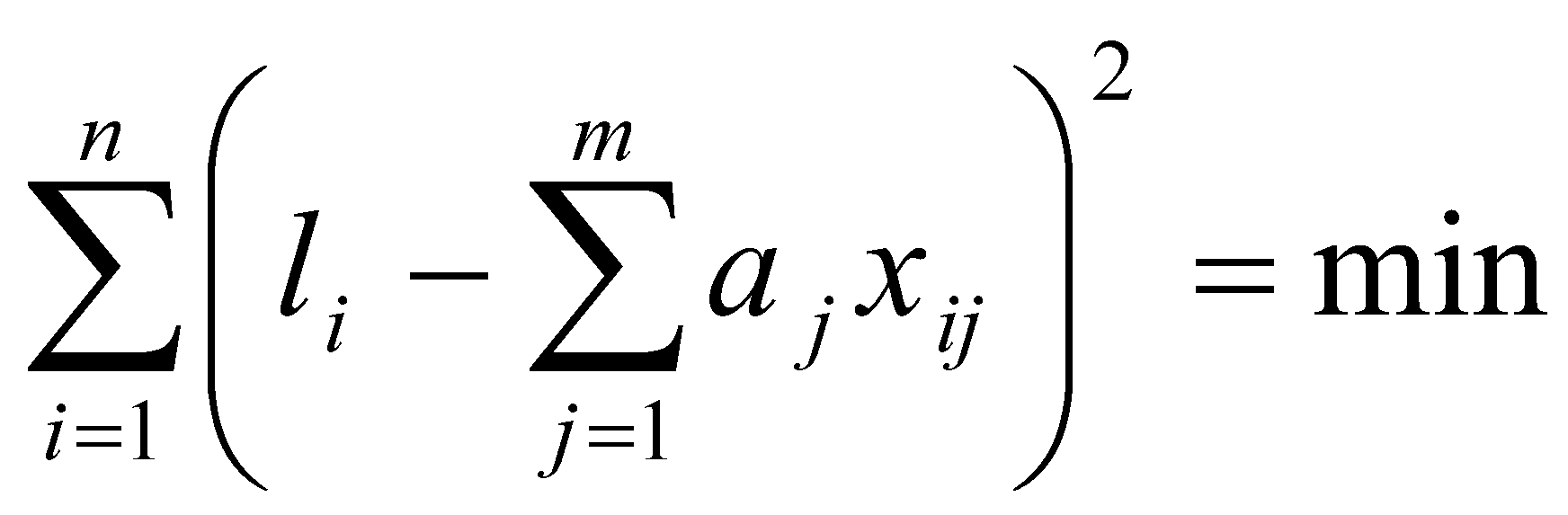 . (38) . (38)Это условие выполняется, если все частные производные от (2.38) по искомым параметрам 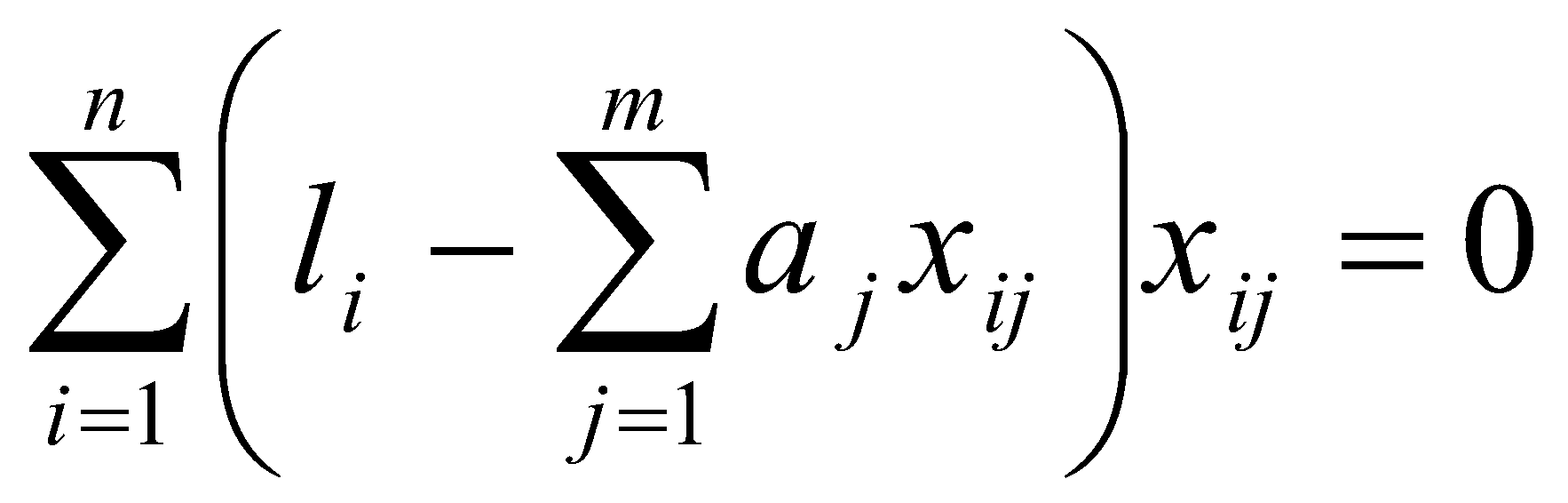 . (39) . (39)Система уравнений (39) линейна относительно Оценка дисперсии случайной погрешности согласно [2.8] будет равна 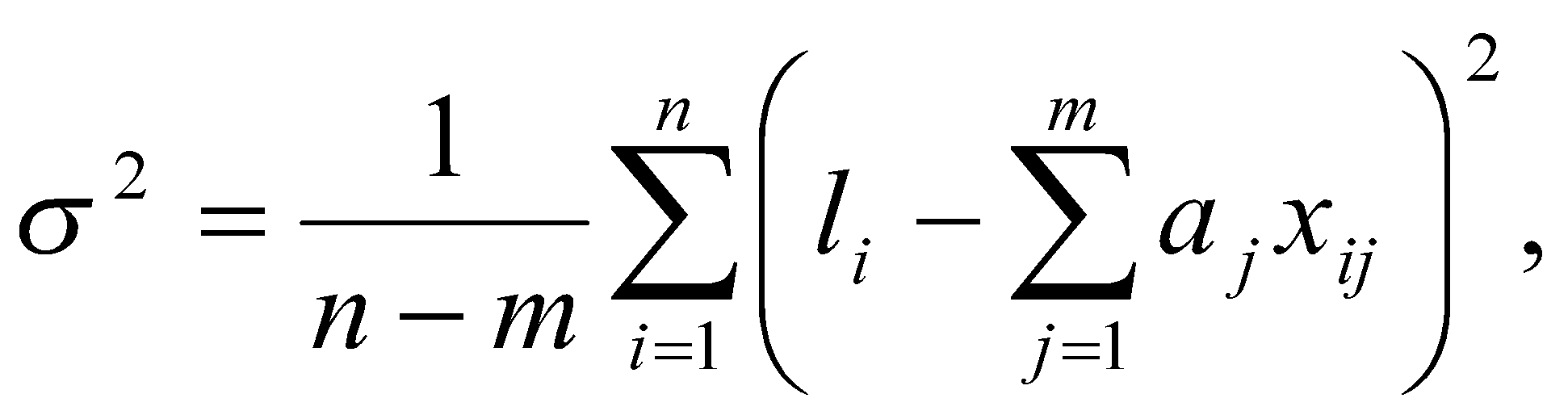 (40) (40)здесь При обработке экспериментального материала с целью определения функции преобразования в качестве математической модели часто выбирают полином вида: а задачей самого измерения является определение коэффициентов Пусть в результате эксперимента получено n пар чисел 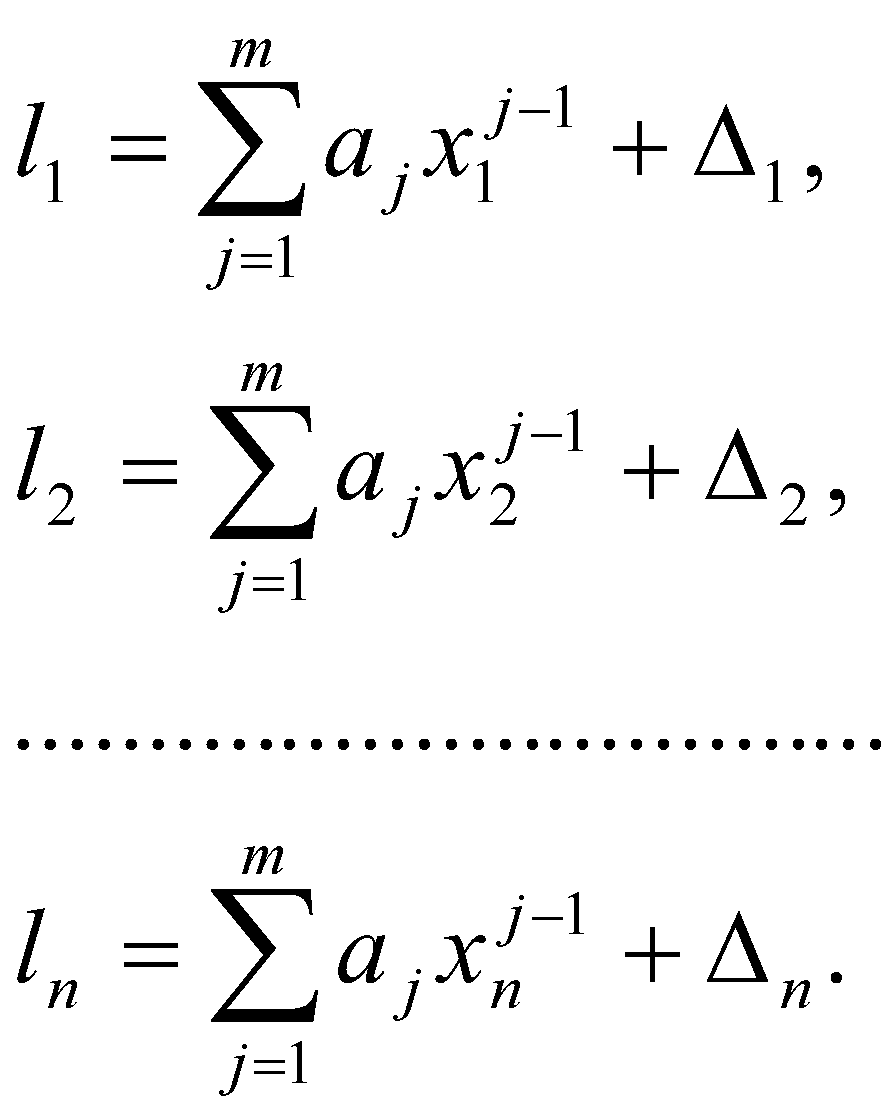 (41) (41)Тогда в соответствии с МНК и учетом (39) получим: 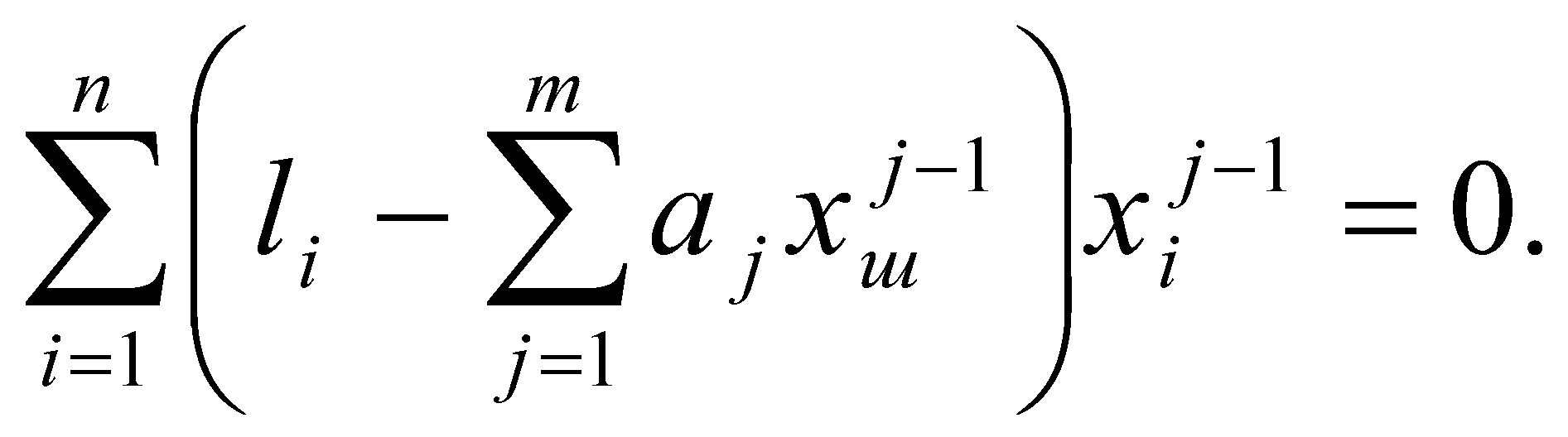 (42) (42)Решение этой системы, линейной относительно 5. Пассивное измерение Если в ходе эксперимента регистрация контролируемых параметров параметров Особенностью пассивного эксперимента являться то, что экспериментатор не может активно воздействовать на исследуемый объект, а сам эксперимент сводится к сбору измерительной информации и ее оптимальной обработке. Задачей пассивного эксперимента чаще всего является построение математической модели объекта. В зависимости от того, как зависят друг от друга факторы и отклики, модель может быть представлена в виде функциональной зависимости (детерминированная модель) или в виде некоторой диффузной модели, параметры которой могут быть только оценены, т.к. вычисляются на основе статистического материала. В результате пассивного эксперимента экспериментатор получает пары чисел xi→ yi( 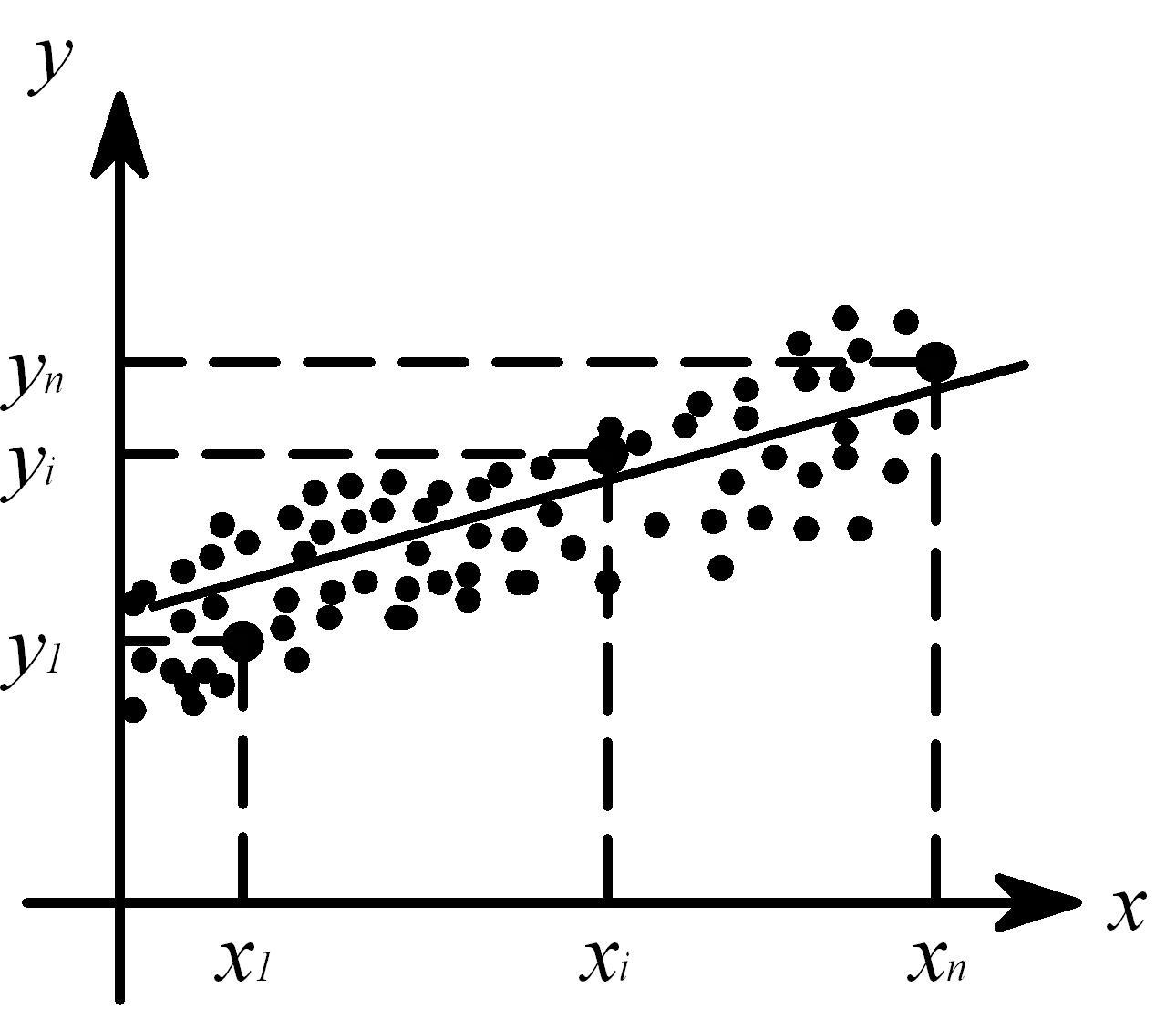 Рис. 10. Графическое изображение уравнения регрессии y=f(x) Учитывая вероятностный характер полученных данных, предполагаемую зависимость При исследовании статистически связанных зависимостей сталкиваются с двумя случаями. В первом случае экспериментатор задает (или просто фиксирует) вполне определенным, детерминированные значения независимой переменной Во втором случае наблюдаемые значения Пусть случайная величина y зависит от одной или нескольких неслучайных величин Уравнением регрессии называют функциональную зависимость математического ожидания М[y] от а регрессивным анализом - процедуру построения уравнения регрессии и анализ его с помощью аппарата математической статистики. Он включает операции оценивания независимых параметров модели, проверки их статистической значимости, проверки адекватности полученной модели исходному статистическому материалу и т. п. Видом (структурой) уравнения задаются заранее, исходя из физической сущности изучаемого явления, анализа накопленного статистического материала, на основании априорной информации. Поэтому непосредственной задачей регрессионного анализа является статистическое оценивание неизвестных параметров постулированной модели. Структура модели определяется видом функции Простая регрессия предполагает наличие одной независимой и одной зависимой переменной т. е. Если число независимых переменных несколько, то регрессия называется множественной. Методами регрессионного анализа можно решать следующие задачи: ∙ описание и установление возможной причинной связи между переменными; ∙ предсказание (экстраполяцию) зависимой переменной по значениям независимой переменной; Рассмотрим простую регрессионную связь. Пусть в результате однофакторного эксперимента получен статистический материал, т. е. выполнено n пар измерений единственного входного сигнала Будем искать математическую модель регрессионной связи в виде степенного полинома где Известно [8], что при правильном выборе степени полинома m такая модель позволяет достаточно точно аппроксимировать истинную зависимость. В соответствии с (2.43) для i-го результата (точки) можно записать Поскольку измерение или 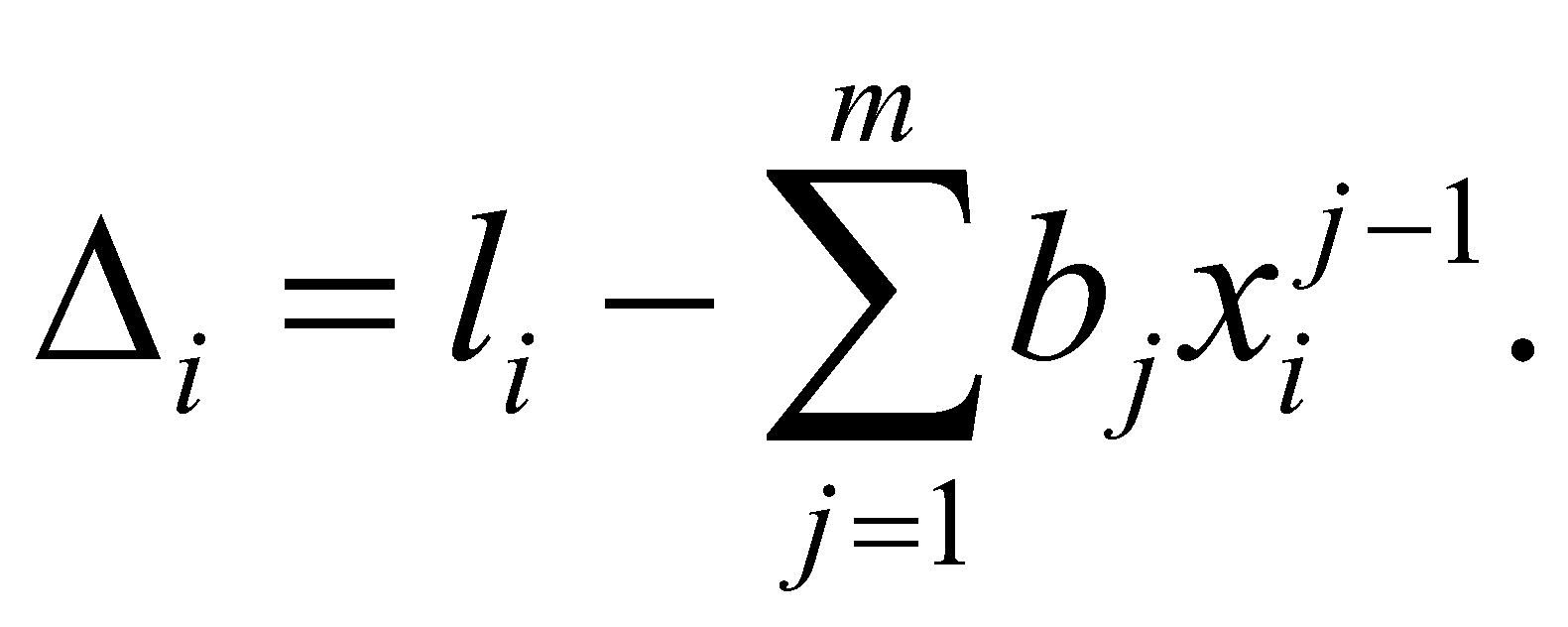 Используя МНК, т. е. выполняя условие получим систему уравнений, линейную относительно искомых параметров j 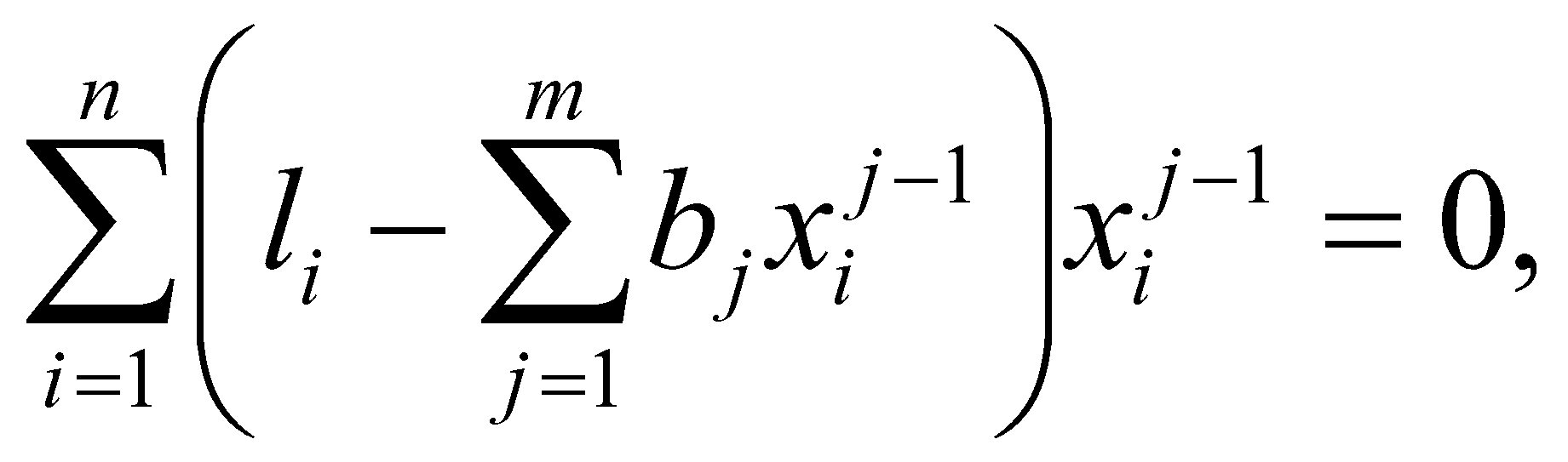 (45) (45)решая которую, получим оценки параметров Очевидно, что полученная модель может лишь с той или иной точностью соответствовать экспериментальной совокупности В качестве меры адекватности может быть использован коэффициент корреляции [3]. 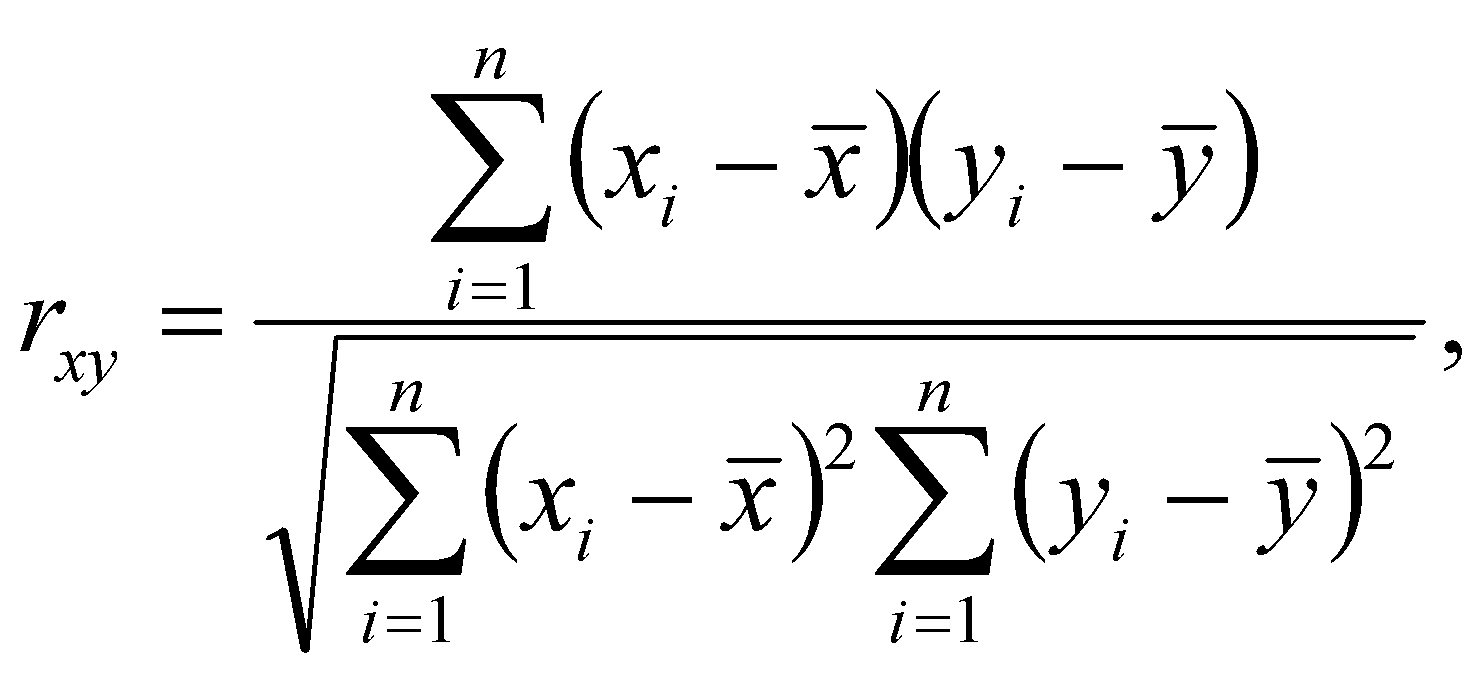 (47) (47)чем ближе Расчёт ТПП. Особенностью пассивного эксперимента являться то, что экспериментатор не может активно воздействовать на исследуемый объект, а сам эксперимент сводится к сбору измерительной информации и ее оптимальной обработке. Задачей пассивного эксперимента чаще всего является построение математической модели объекта. В результате пассивного эксперимента экспериментатор получает пары чисел xi→ yi( При исследовании статистически связанных зависимостей сталкиваются с двумя случаями. В первом случае экспериментатор задает (или просто фиксирует) вполне определенным, детерминированные значения независимой переменной, для которых наблюдается соответствующие случайные значения, определяемые своими статистическими характеристиками: оценкой математического ожидание и СКО. В этом случае модель называется регрессионной. Уравнением регрессии называют функциональную зависимость математического ожидания М[y], а регрессивным анализом - процедуру построения уравнения регрессии и анализ его с помощью аппарата математической статистики. Результаты измерений:
Где 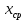 определяется по формуле: определяется по формуле: 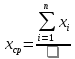 , где n=6 , где n=6Составим систему уравнений вида: y=a+b*x. Получим: { 0,27=a+50*b; {0,35=a+60*b; {0,45=a+70*b; {0,53=a+80*b; Решая эту систему получим что b=0,008=const; 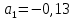 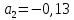 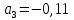 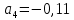 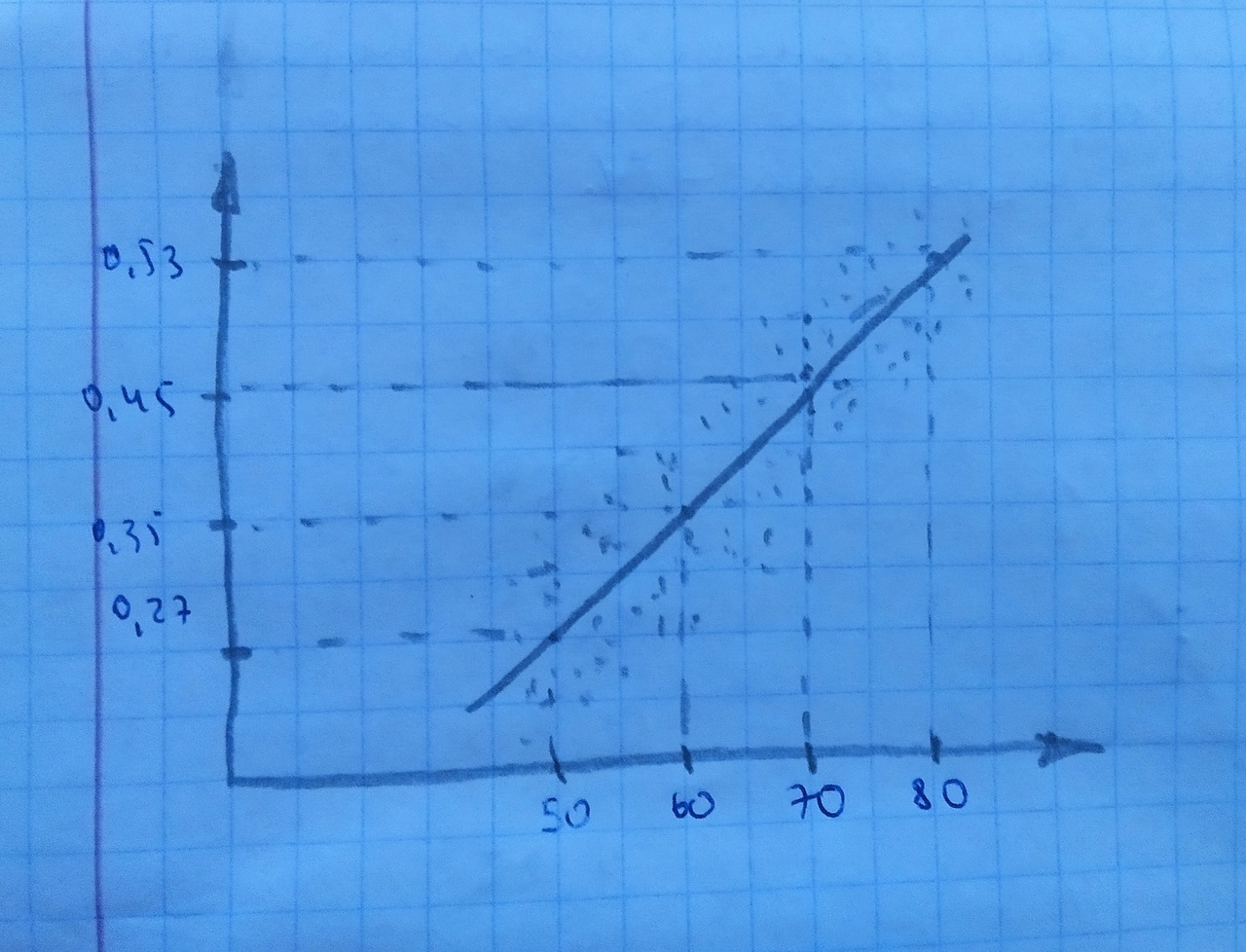 6. Активный многофакторный эксперимент (постановка задачи, смысл, статистическая обработка) Активный эксперимент подразумевает использование специальных, целенаправленных возмущений (воздействий) Х по заранее определенной программе. Каждый способ получение информации имеет свои недостатки и преимущества. Так, например, активный эксперимент не всегда можно осуществить на любом объекте, т. к. это может привести к аварийным ситуациям |
