Численные методы и методы оптимизации. чмимо отчет 2. Отчет по лабораторным работам по дисциплине Численные методы и методы оптимизации

• Название: Отчет по лабораторным работам по дисциплине Численные методы и методы оптимизации
• Анкор: Численные методы и методы оптимизации
• Дата: 01.10.2022
• Размер: 51.72 Kb.
• Имя файла: чмимо отчет 2.docx
• Тип: Отчет; #708245

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ

РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное

образовательное учреждение высшего образования

«Самарский национальный исследовательский университет

имени академика С.П. Королёва»

(Самарский университет)
Институт авиационной и ракетно-космической техники
Отчет по лабораторным работам по дисциплине

«Численные методы и методы оптимизации»


WS32

Выполнил

студент гр. 1306-240501D

Астайкина А.С.

Проверил

Пупков Е. А.

Самара 2022

Лабораторная работа №2

Интерполирование функции с помощью формулы Лагранжа
Интерполяционная формула Лагранжа имеет следующий вид: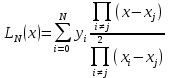

.

В качестве исходных данных используются координаты 10 точек

(i = 0..9), заданные вручную в таблице 1.

Таблица 1 – Исходные данные

i	0	1	2	3	4	5	6	7	8	9	10
x	0	0.2	0.35	0.45	0.5	0.7	0.85	0.9	1.0	1.1	1.45
y	8	7	3	4	8	1.5	6	9	10	5	1

В формуле Лагранжа при раскрытии знака суммирования получится 11 слагаемых, которые обозначим через Q0(t), …, Q10(t). Формулы для их вычисления представлены ниже: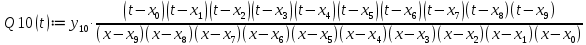


;

;

;
; ; ; ; ; ; .


Запишем итоговую формулу:

Q(t) = Q0(t)+ Q1(t)+ Q2(t)+ Q3(t)+ Q4(t)+ Q5(t)+ Q6(t) )+ Q7(t)+ Q8(t)+ Q9(t)+Q10(t).

В результате операции simplify получим интерполяционный полином Лагранжа:









Рисунок 1.1 – График полинома Лагранжа

Как видно из рисунка 1.1, график интерполирующего полинома проходит через заданные точки, то есть решение получено верно.