Лаба 4. Отчет по лабораторнопрактической работе 4 Исследование динамики вращательного движения твердого тела

• Название: Отчет по лабораторнопрактической работе 4 Исследование динамики вращательного движения твердого тела
• Дата: 24.02.2021
• Размер: 0.53 Mb.
• Имя файла: Лаба 4.doc
• Тип: Отчет; #179061
• страница: 1 из 2

Санкт-Петербургский государственный электротехнический университет

“ЛЭТИ”

кафедра физики

ОТЧЕТ

по лабораторно-практической работе № 4

«Исследование динамики вращательного движения твердого тела»

Выполнила Карелина Л.А.

Факультет КТИ

Группа № 7373

Преподаватель Шахова

Оценка лабораторно-практического занятия
Выполнение ИДЗ	Подготовка к лабораторной работе	Отчет по лабораторной работе	Коллоквиум		Комплексная оценка

“Выполнено” “____” ___________

Подпись преподавателя __________

ЛАБОРАТОРНАЯ РАБОТА № 4

«Исследование динамики вращательного движения твердого тела»

ЦЕЛЬ РАБОТЫ: исследование динамики вращательного движения твердого тела на примере крутильного маятника, определение моментов инерции твердых тел.

Приборы и принадлежности: крутильный маятник, секундомер.

С 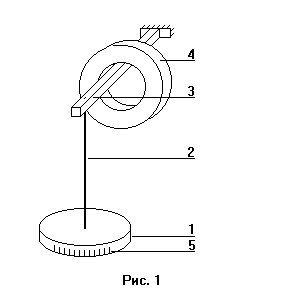ХЕМА УСТАНОВКИ:

Применяемый в работе крутильный маятник (рис. 1) представляет собой диск 1, закрепленный на упругой стальной проволоке 2, свободный конец которой зажат в неподвижном кронштейне 3. На кронштейне расположено кольцо 4, масса которого известна. Кольцо 4 можно положить сверху на диск 1, изменив тем самым момент инерции маятника. На диске 1 установлен флажок, располагающийся под подставкой макета в ванночке с жидкостью. Поворачивая флажок, можно изменять момент сил сопротивления, действующих на маятник. Для отсчета значений угла поворота маятника служит градуированная шкала 5, помещенная на ободе диска 1.

ИССЛЕДУЕМЫЕ ЗАКОНОМЕРНОСТИ:

Крутильный маятник. При повороте тела, закрепленного на упругом подвесе, в результате деформации сдвига при закручивании подвеса возникает возвращающий момент упругих сил M = k, где k - коэффициент кручения, зависящий от упругих свойств материала подвеса, его размеров и формы,  - угол поворота. При малых углах поворота, без учета сил трения в подвесе, крутильные колебания маятника являются гармоническими, а уравнение движения тела имеет вид
,

где частота собственных колебаний гармонического осциллятора

,

I – момент инерции диска крутильного маятника.

Сопротивление движению маятника (трение) создает тормозящий момент, пропорциональный скорости движения маятника,

,

где R - коэффициент сопротивления. С учетом сил сопротивления уравнение движения маятника принимает вид


и является уравнением движения осциллятора с затуханием. Колебания такого осциллятора уже не будут гармоническими. Коэффициент  = R/2I называют коэффициентом затухания. Если , движение крутильного маятника описывается уравнением затухающих колебаний

,

где - начальная амплитуда колебаний маятника,  = 1/ - время затухания, определяющее скорость убывания амплитуды A(t) маятника, численно равное времени, за которое амплитуда убывает в e раз (рис. 2), т.е.

при t =  ,  - частота колебаний осциллятора с затуханием, связанная с собственной частотой соотношением . Время затухания  также выражается через момент инерции I и коэффициент сопротивления R выражением .

Момент инерции крутильного маятника

Момент инерции – физическая величина, характеризующая инертные свойства твердого тела при его вращении. В соответствии с одной из формулировок основного уравнения динамики вращательного движения

,

момент инерции (I) связывает угловое ускорение тела () и момент сил (M), действующих на него.

Если твердое тело вращается вокруг неподвижной оси, то момент инерции относительно этой оси вычисляется как сумма произведений элементарных масс m_i, составляющих тело, на квадраты их расстояний (r_i) до оси вращения, т.е.

,

где  - плотность тела, V_i – элементы объема. Таким образом, момент инерции является аддитивной величиной.

Крутильный маятник совершает колебательное движение. Тем не менее, за время, меньшее, или равное половине периода его колебаний, движение маятника между двумя крайними положениями (максимальными углами поворота по- и против часовой стрелки) является вращательным. Поэтому, используя уравнение движения крутильного маятника и основное уравнение динамики вращательного движения, можно определить момент инерции маятника, а также все характерные физические величины, описывающие вращательное движение. В данной работе экспериментально определяется момент инерции диска крутильного маятника.

ЗАДАНИЕ ПО ОБРАБОТКЕ РЕЗУЛЬТАТОВ:

1. 
   Вычислим периоды колебаний маятника с кольцом T_к :
   

Расчетная формула: Т_к= , где t_к– время, за которое совершались колебания, n=10 – количество колебаний, совершенных маятником.

T_к1= =1,312 (сек)

Т_к2= =1,356 (сек)

Т_к3= =1,378 (сек)

Т_к4= =1,356 (сек)

Т_к5= =1,340 (сек)

Определяем погрешности ∆T с доверительной вероятностью p = 95%.

Упорядочим выборку объемом N=5:

T_кmin=1,312 1,340 1,356 1,356 1,378=T_{к max}

R_Tк = T_{к max} – T_{к min} = 1,378-1,312=0,066 (сек)

Проверка на промахи:

промаха нет

промаха нет.

По результатам проведенных расчетов заключаем, что в нашей выборке промахи отсутствуют. Продолжаем далее статистическую обработку.

Рассчитываем среднее по формуле

_к= 1,3484 (сек)

Рассчитываем СКО среднего по формуле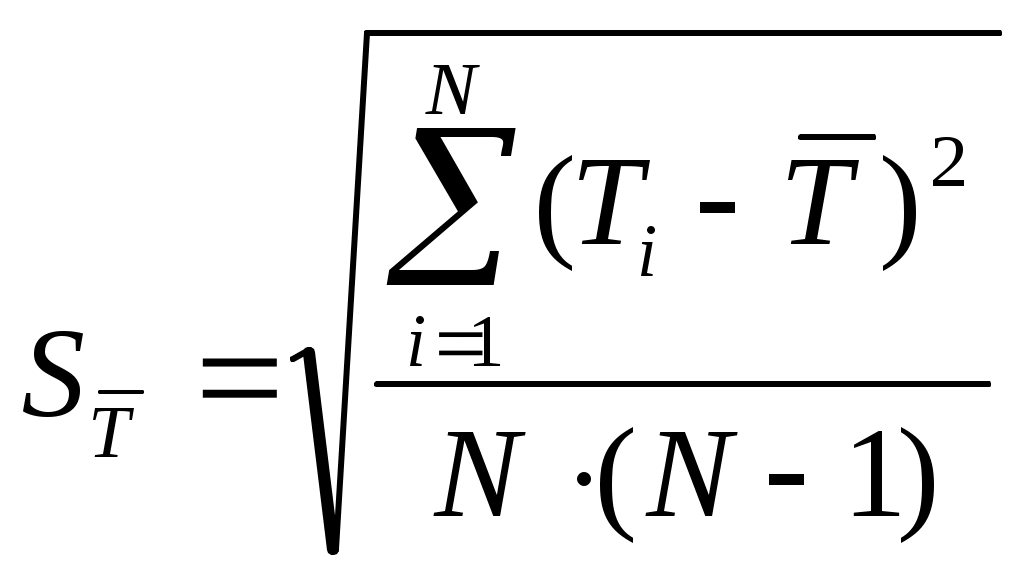

= 0,0109 (сек)

Расчет случайной погрешности по формуле
при N=5, t_p,N =2.8, p=95%.

(сек)

Найдем приборную погрешность , где (сек) – цена деления секундомера

=0,005 (сек)

Вычислим полную погрешность

= 0,0309 (сек)

Запишем результат статистической обработки с p=95%

T_к=1,35 0,03 (сек) сp=95%

2. 
   Вычислим периоды колебаний маятника без кольца T_д :
   

Расчетная формула: Т_д= , где t_д– время, за которое совершались колебания, n=10 – количество колебаний, совершенных маятником.

T_д1= =0,984 (сек)

T_д2= =0,973 (сек)

T_д3= =1,000 (сек)

T_д4= =0,996 (сек)

T_д5= =0,969 (сек)

Определяем погрешности ∆T_д с доверительной вероятностью p = 95%.

Упорядочим выборку объемом N=5:

T_дmin=0,969 0,973 0,984 0,996 1,000=T_{д max}

R_д= T_дmax – T_{д min} = 1,000-0,969=0,031 (сек)

Проверка на промахи:

промаха нет

промаха нет.

По результатам проведенных расчетов заключаем, что в нашей выборке промахи отсутствуют. Продолжаем далее статистическую обработку.

Рассчитываем среднее по формуле

= 0,9844 (сек)

Рассчитываем СКО среднего по формуле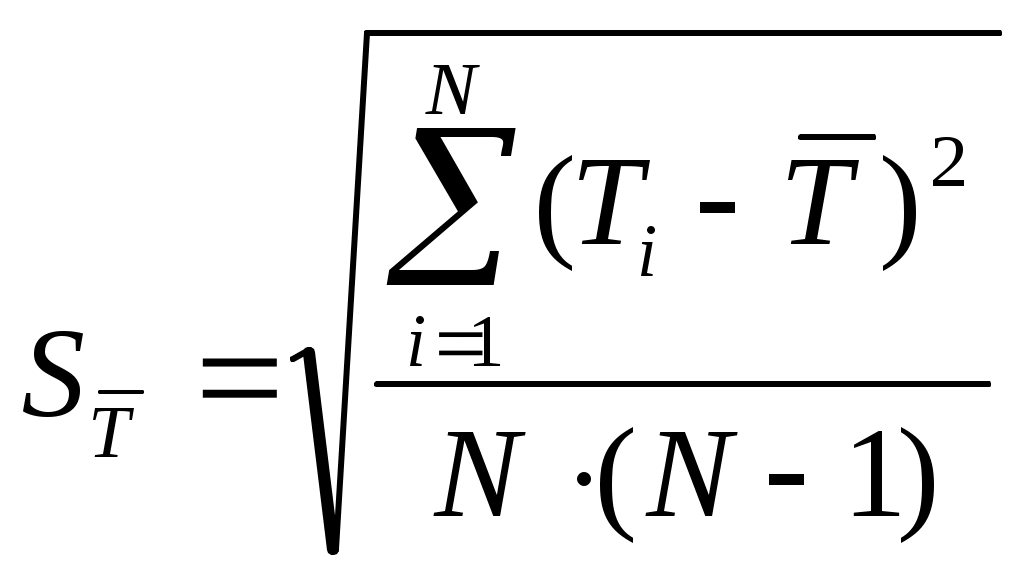

= 0,006 (сек)

Расчет случайной погрешности по формуле
при N=5, t_p,N =2.8, p=95%.

(сек)

Найдем приборную погрешность , где (сек) – цена деления секундомера

=0,005 (сек)

Вычислим полную погрешность

= 0,0175 (сек)

Запишем результат статистической обработки с p=95%

T_д=0,984 0,018 (сек) сp=95%

3. 
   Вычислим частоты колебаний _к и _д для маятника с кольцом и без кольца:
   

Расчетная формула: = , где Т – период колебаний.

С кольцом:

_к1= =4,7866 (сек^-1)

_к2= =4,6313 (сек^-1)

_к3= =4,5573 (сек