Отчет по лабораторной работе " Дискретизация сигналов" по дисциплине " Цифровая обработка сигналов"
 Скачать 425.84 Kb. Скачать 425.84 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное ГОСУДАРСТВЕННОЕ бюджетное ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «ПОВОЛЖСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ» Отчет по лабораторной работе “ Дискретизация сигналов” по дисциплине “ Цифровая обработка сигналов” Выполнил: студент гр. Проверил:Йошкар-Ола 2018 г. Цель работы: 1) Изучить вопросы аналого-цифрового и цифро-аналогового преобразования сигналов. 2) Исследовать процедуру дискретизации и восстановления аналоговых сигналов.
Аналоговый сигнал 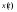 является вещественнозначной функцией вещественного непрерывного аргумента (времени), источниками которого служат различные физические процессы и явления, непрерывно меняющиеся во времени (или в пространстве). является вещественнозначной функцией вещественного непрерывного аргумента (времени), источниками которого служат различные физические процессы и явления, непрерывно меняющиеся во времени (или в пространстве).Дискретный сигнал 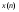 – это кусочно-непрерывная вещественнозначная функция дискретного аргумента – это кусочно-непрерывная вещественнозначная функция дискретного аргумента  . Дискретный сигнал представляет собой набор отсчетов некоторой величины, измеренной в дискретные моменты времени. Интервал . Дискретный сигнал представляет собой набор отсчетов некоторой величины, измеренной в дискретные моменты времени. Интервал 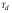 между двумя соседними отсчетами называется шагом дискретизации, а обратная величина между двумя соседними отсчетами называется шагом дискретизации, а обратная величина 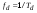 – частотой дискретизации. – частотой дискретизации.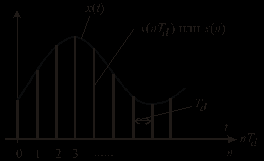 Рис. 1. Графики непрерывного 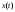 и дискретного и дискретного 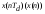 сигналов сигналовПри дискретизации аналогового сигнала с финитным спектром, ограниченным максимальной частотой 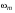 , отвечающей условию , отвечающей условию 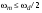 (рис. 1.2), спектр дискретного сигнала (рис. 1.2), спектр дискретного сигнала 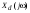 в основной полосе частот в основной полосе частот 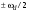 (при (при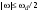 ) точно совпадает (до постоянного множителя ) точно совпадает (до постоянного множителя 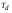 ) со спектром аналогового сигнала: ) со спектром аналогового сигнала:  . Условие . Условие 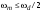 (или (или 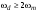 ) отвечает теореме отсчетов Котельникова. ) отвечает теореме отсчетов Котельникова. Сигнал на выходе ФНЧ соответствует обратному преобразованию Фурье депериодизированного спектра дискретного сигнала 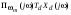 : :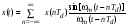 Интервал между уровнями квантования называется шагом квантования по уровню 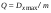 . .Квантование возможно с усечением и с округлением. Квантованный дискретный сигнал 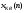 определяется: определяется:
 ; ;
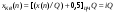 , , где  − это целая часть заключенного в скобки отношения, соответствующая номеру уровня квантования, с которым отождествляется точное значение квантуемого дискретного сигнала: с ближайшим меньшим − при усечении и ближайшим – при округлении. Для однополярного сигнала − это целая часть заключенного в скобки отношения, соответствующая номеру уровня квантования, с которым отождествляется точное значение квантуемого дискретного сигнала: с ближайшим меньшим − при усечении и ближайшим – при округлении. Для однополярного сигнала 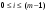 , для двухполярного , для двухполярного 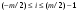 . .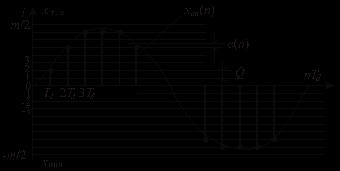 Рис. 2. Иллюстрация квантования сигнала по уровню Восстановление аналогового сигнала из дискретного возможно, если шаг дискретизации удовлетворяет теореме Котельникова.
1. Провести исследование восстановления сигнала из дискретной и цифровой выборки в зависимости от шага дискретизации. Параметры сигнала в соответствии с вариантом представлены в табл. 1. Построить графики исходного (аналогового), дискретизированного, цифрового и восстановленного сигналов для нескольких значений частоты дискретизации и числа уровней квантования (разрядности 8, 12, 16). 2. Исследовать зависимости погрешности восстановления сигналов от частоты дискретизации и числа уровней квантования (разрядности). Таблица 1.
1) Задание переменных 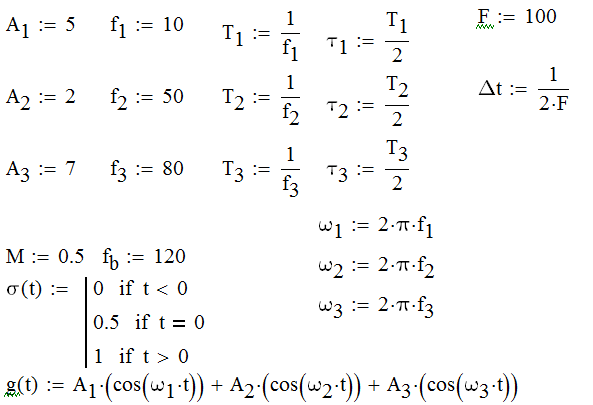 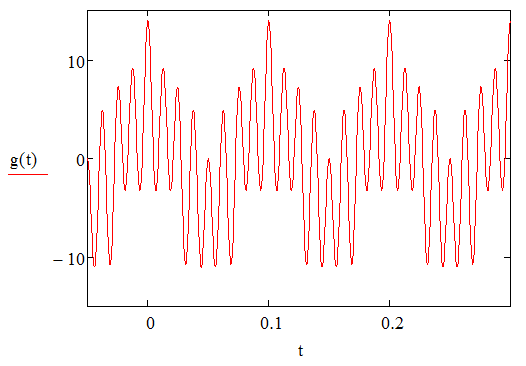 Рис. Исходный сигнал (аналоговый)   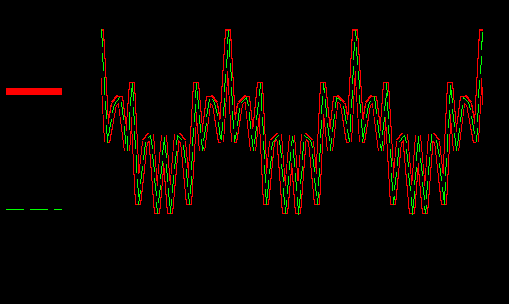   Аналоговый g(t) и восстановленный S(t) сигналы – F=100 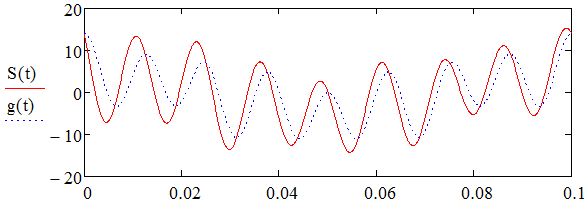 Аналоговый g(t) и восстановленный S(t) сигналы – F=80
1) Задание переменных 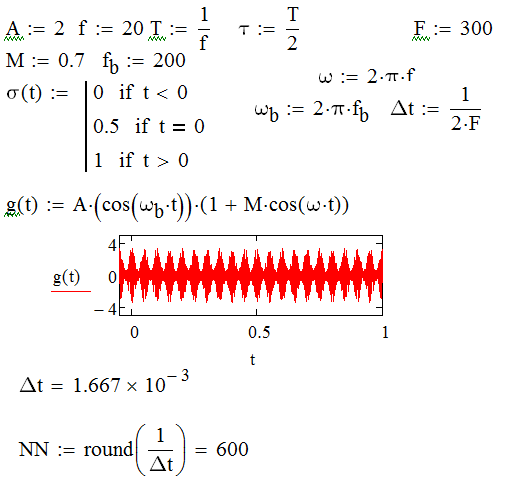  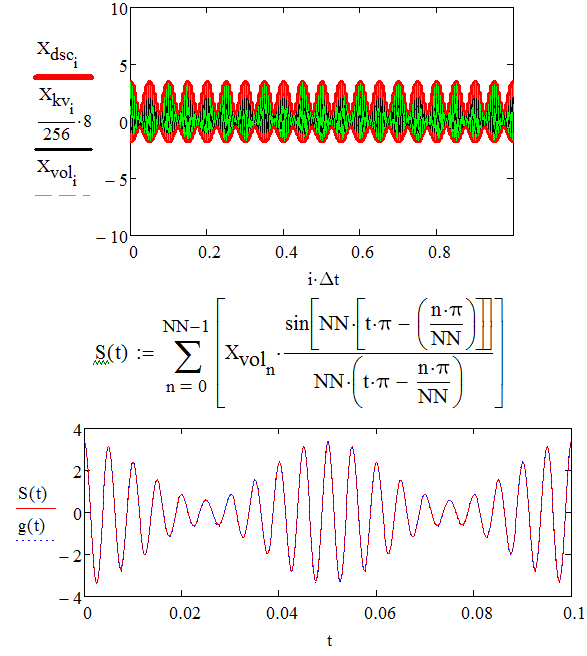 Аналоговый g(t) и восстановленный S(t) сигналы – F=300 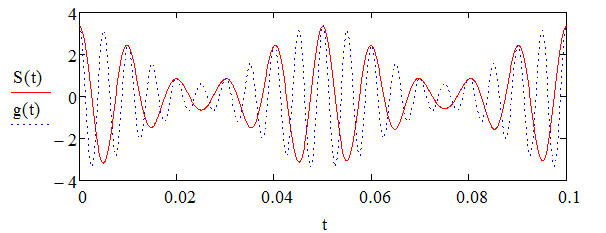 Аналоговый g(t) и восстановленный S(t) сигналы – F=150
1) Задание переменных 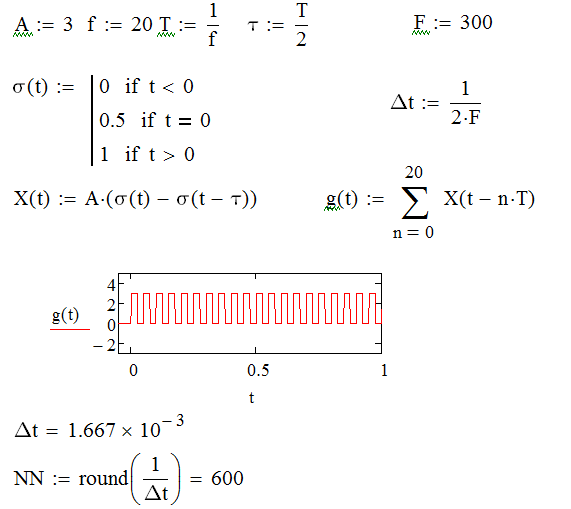 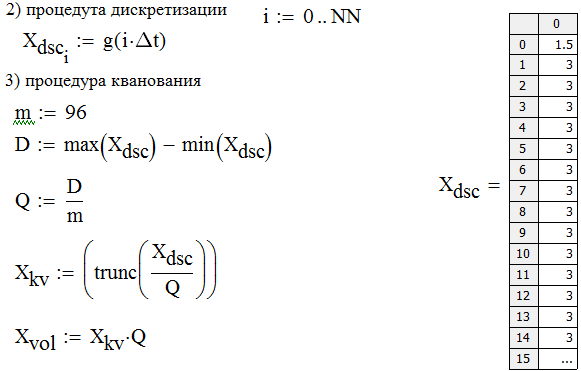 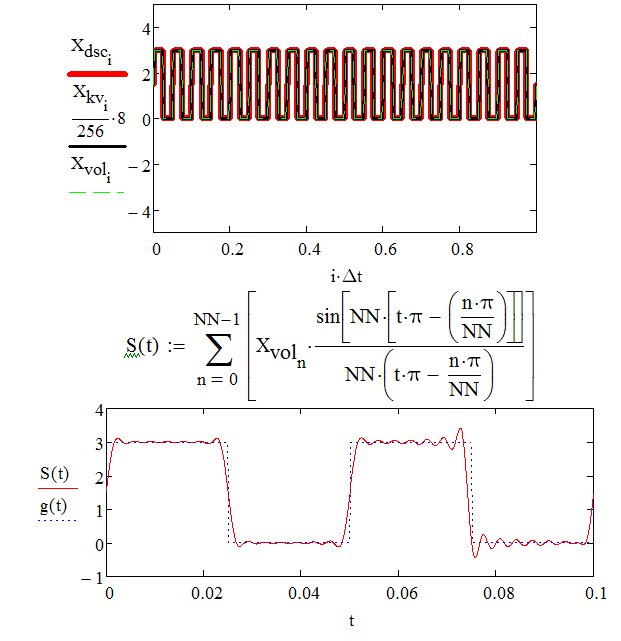 Аналоговый g(t) и восстановленный S(t) сигналы – F=300 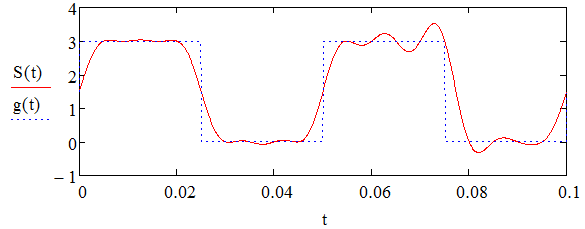 Аналоговый g(t) и восстановленный S(t) сигналы – F=100
1) Задание переменных   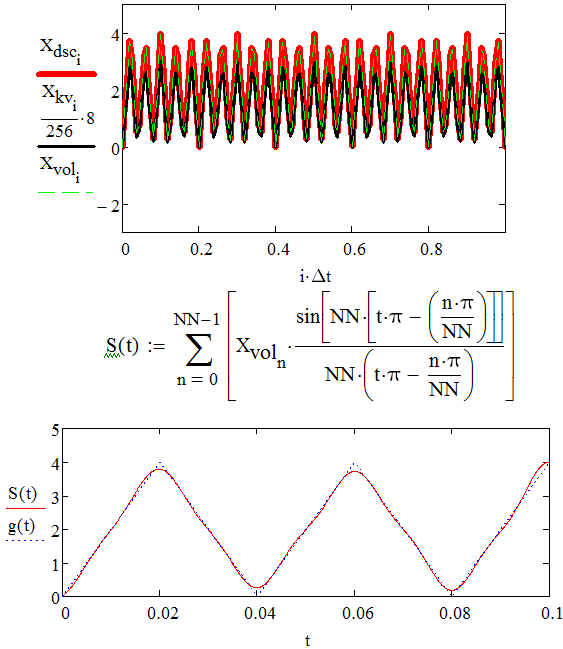 Аналоговый g(t) и восстановленный S(t) сигналы – F=80 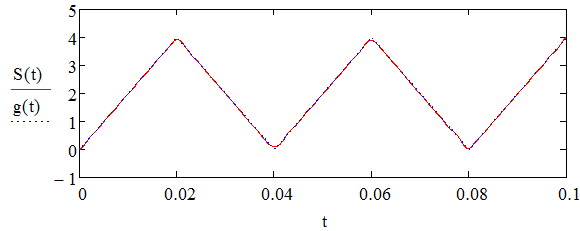 Аналоговый g(t) и восстановленный S(t) сигналы – F=320 Погрешности:
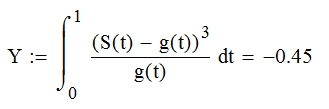 Полигармонический сигнал F=80 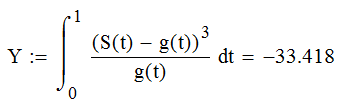
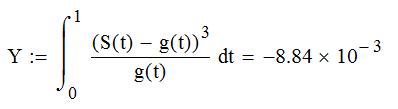 АМ-сигнал F=150 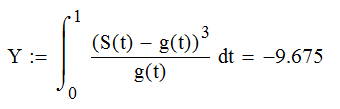
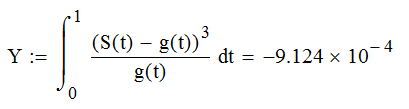
 Вывод: Изучили вопросы аналого-цифрового и цифро-аналогового преобразования сигналов. Исследовали процедуру дискретизации, квантования и восстановления аналоговых сигналов. Выяснили, что при увеличении частоты дискретизации и уровней квантования уменьшается погрешность, при их уменьшении – погрешность возрастает. Оптимальную частоту дискретизации и число уровней квантования можно определить по теореме Котельникова. | ||||||||||||||

 ,
,  ,
,  ,
, 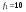 Гц,
Гц, 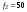 Гц,
Гц, 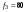 Гц.
Гц.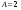 ,
, 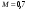 ,
, 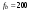 Гц,
Гц, 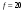 Гц.
Гц.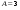 ,
, 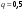 .
.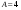 ,
, 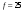 Гц.
Гц.