Матричные преобразования и трехмерная графика» по дисциплине «Математические основы теории систем. ОтчЕт по лабораторной работе 1 Матричные преобразования и трехмерная графика
 Скачать 0.68 Mb. Скачать 0.68 Mb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра АПУ отчЕт по лабораторной работе №1 «Матричные преобразования и трехмерная графика» по дисциплине «Математические основы теории систем»
Санкт-Петербург 2021 Цель работы: освоение специфики матричных преобразований MATLAB и сравнительный анализ различных форм графического отображения результатов. Выполнение работы. Задание 1: В качестве исходной фигуры для выполнения лабораторной работы, на которой мы будем изучать матричные преобразования, выберем пирамиду. Присвоим этой матрице имя R. Симметрия выбранной матрицы R относительно главной ее диагонали и антидиагонали делает такую матрицу вырожденной, это значит что ее определитель должен быть равен нулю. Затем мы выполняем проверку того что определитель у выбранной нами матрицы равен нулю. Соответственно, исходя из вышеперечисленных утверждений, большинство матричных операций для этой матрицы невыполнимо. Добавим к элементам матрицы на главной ее диагонали по единице, затем складываем ее с единичной матрицей (eye) того же размера, то есть равной единице. Теперь над выбранной нами матрицей можно производить как поэлементные, так и матричные операции.  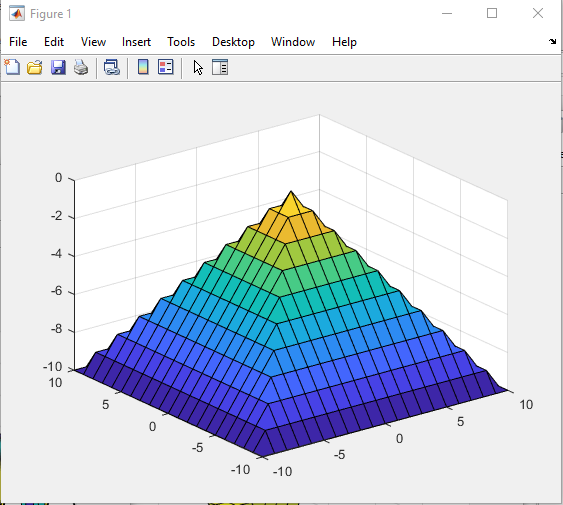 Рис.1 Построение пирамиды Задание 2: Сравниваем по имеющимся графикам результаты двух выполненных операций – это обращения матрицы командой inv и поэлементного деления матрицы ones(n,n) на R.  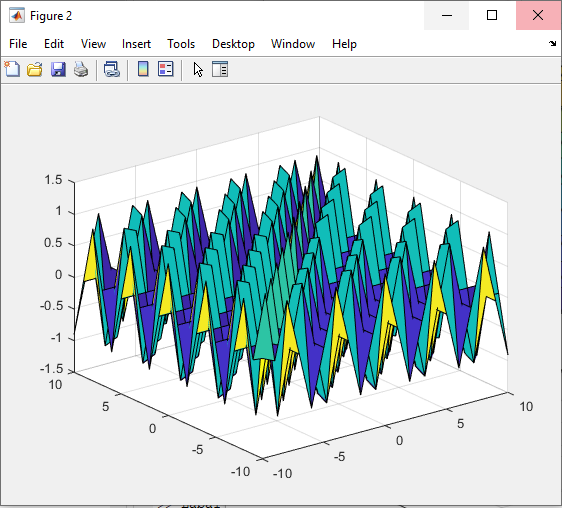 Рис.2 Обращения матрицы командой inv  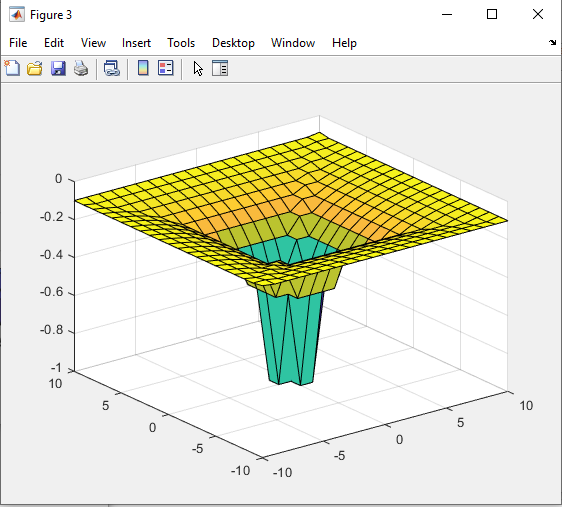 Рис.3 Поэлементное деление матрицы Задание 3: Затем сравниваем матричные операции sqrtm(A), logm(A), expm(A) с аналогичными операциями, выполняемыми поэлементно.   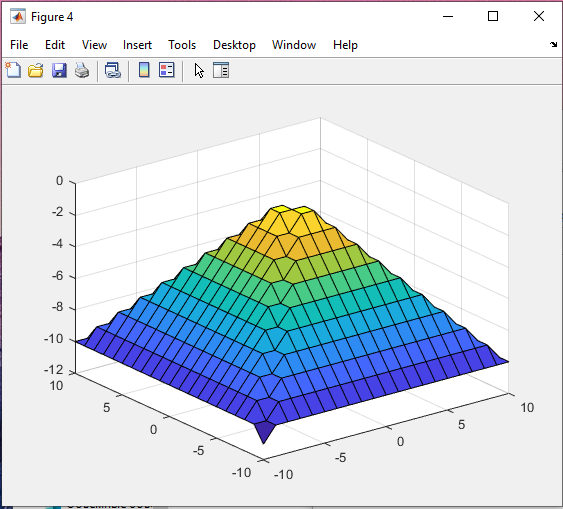 Рис.4 Матричная операция sqrtm(R) 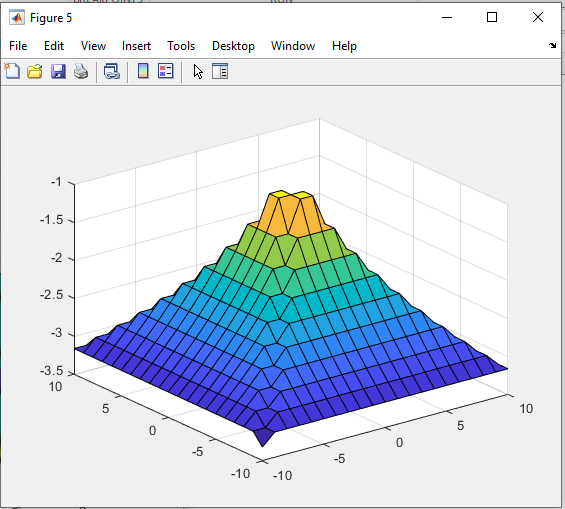 Рис.5 Поэлементное выполнение операции sqrtm 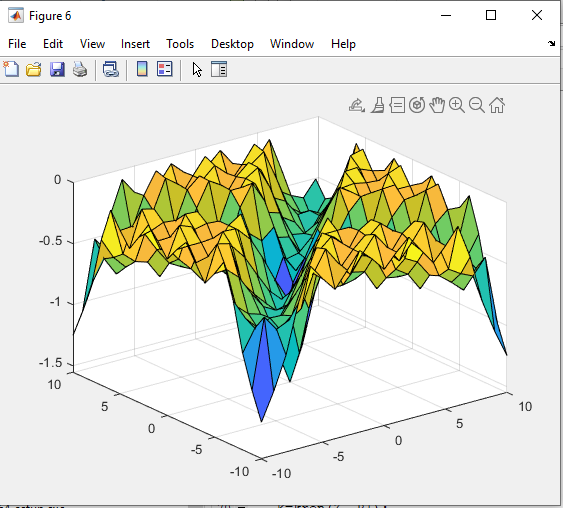 Рис.6 Матричная операция logm(R) 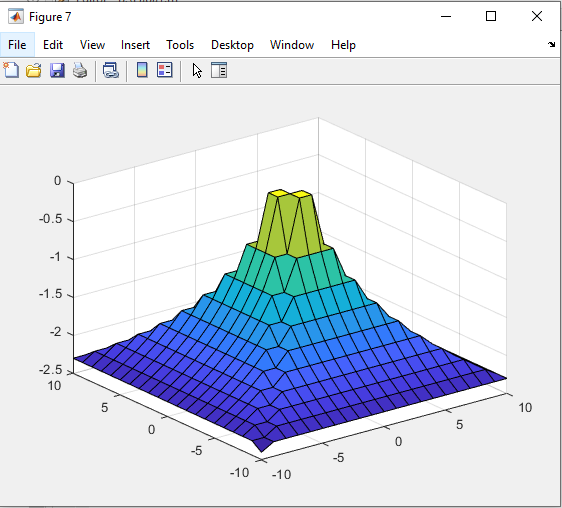 Рис.7 Поэлементное выполнение операции logm 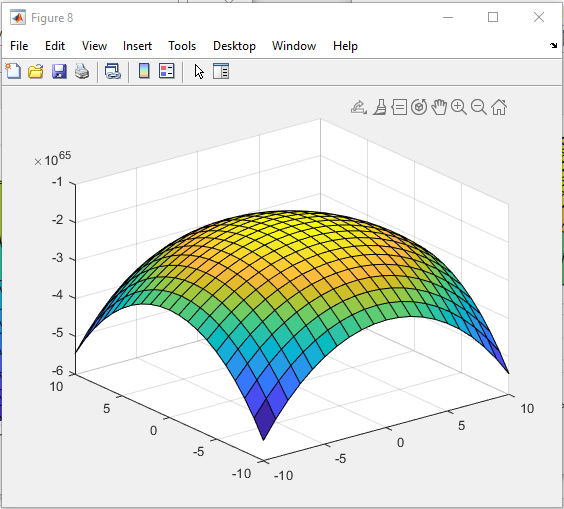 Рис.8 Матричная операция expm(R) 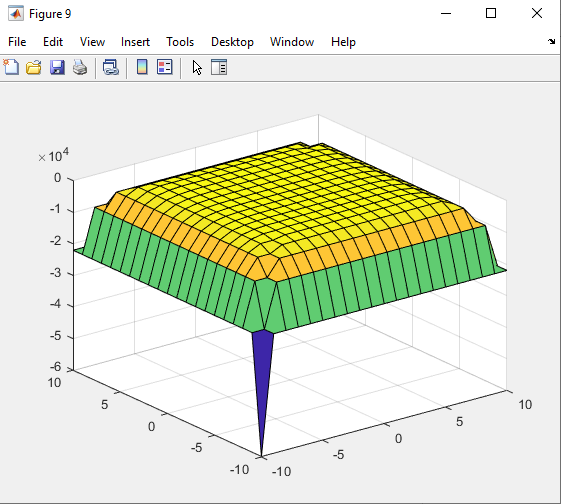 Рис.9 Поэлементное выполнение операции expm Задание 4: Преобразуем имеющуюся пирамиду R с помощью операций врезки. Отрезаем какой-нибудь из углов, имеющихся в пирамиде. Одновременно приравниваем нулю выбранные элементы.  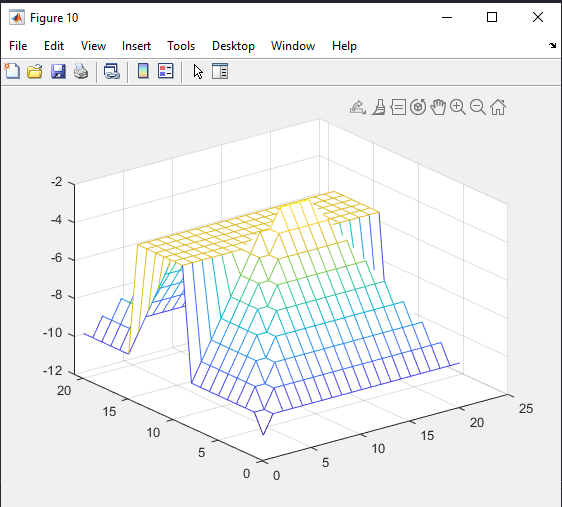 Рис.10 Операция врезки Задание 5: Очень полезной и важной операцией размножения ( иными словами мультиплицирования) массивов является операция кронеревского умножения матриц, в которой вся правая матрица умножается на каждый элемент левой матрицы.  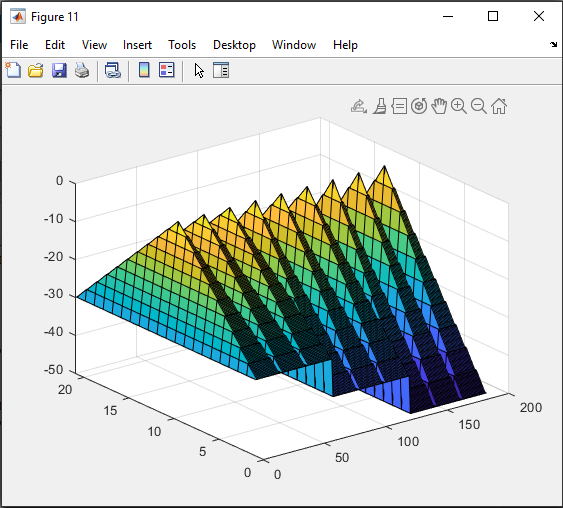 Рис. 11 Кронеревское умножение матриц Выводы: В данной лабораторной работе, путем работы с исходно предоставленной фигурой были изучены матричные преобразования. А именно - поэлементные и матричные операции, сравнения графиков выполненных операций, обращения матрицы и ее поэлементарного деления. Так же были изучены матричные операции sqrtm(A), logm(A), expm(A) с их аналогичными операциями. Освоена была операция врезки пирамиды, и операция размножения массивов путем умножения матриц. Все теоретически полученные навыки были подкреплены практическим выполнением заданий на эту тему, что позволило в полной мере изучить данный материал. |
