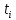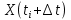Отчет. отчет 1 лабораторная работа. Отчет по лабораторной работе 1 По дисциплине Моделирование Принципы построения моделирующих алгоритмов и
 Скачать 140.21 Kb. Скачать 140.21 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ государственное БЮДЖЕТНОЕ образовательное учреждение высшего образования «НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Отчет по лабораторной работе №1 По дисциплине «Моделирование» «Принципы построения моделирующих алгоритмов: 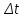 и и 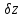 » »
Новосибирск 2023 Цель работы: - изучить принципы построения моделирующих алгоритмов: принцип 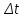 и принцип особых состояний и принцип особых состояний 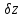 ; ;- приобрести навыки построения имитационных моделей согласно принципам 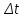 и и 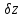 на примере моделирования работы простейших систем. на примере моделирования работы простейших систем. Задание: Постановка задачи к п. 1: Рассчитать значения производной 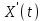 детерминированной функции детерминированной функции 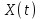 (в соответствии с вариантом, табл. 1), подаваемой на вход дифференцирующего фильтра. (в соответствии с вариантом, табл. 1), подаваемой на вход дифференцирующего фильтра.
Таблица 1. Исходные данные Постановка задачи, выполнение работы 3.1. Рассчитать значения производной 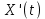 детерминированной функции детерминированной функции 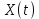 , подаваемой на вход дифференцирующего фильтра. , подаваемой на вход дифференцирующего фильтра.3.1.1. Рассчитать 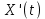 имитационным методом на основе принципа Δt в моменты времени имитационным методом на основе принципа Δt в моменты времени 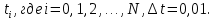 3.1.2. Рассчитать значения производной 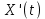 в моменты времени в моменты времени 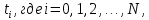 используя аналитическую формулу (аналитический метод). используя аналитическую формулу (аналитический метод).3.1.3. Построить графики исходной функции 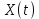 и производных и производных 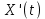 , рассчитанных имитационным методом и аналитическим. Сопоставить полученные результаты, сделать выводы. , рассчитанных имитационным методом и аналитическим. Сопоставить полученные результаты, сделать выводы.Выполним пункт 3.1 в программе Excel (ниже приведён фрагмент таблицы, в оригинале 50 строк). Для имитационного метода использовалась формула  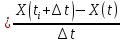  Для аналитического метода использовалась формула Для аналитического метода использовалась формула 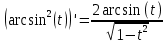 Фрагмент таблицы с результатами:
Таблица 2. Фрагмент результатов выполнения п. 3.1 Графики функции 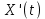 , рассчитанных имитационным методом и аналитическим. , рассчитанных имитационным методом и аналитическим.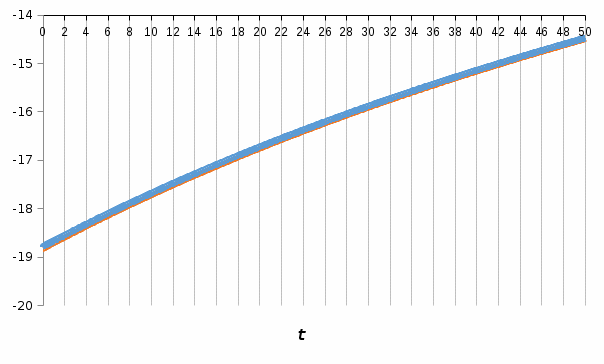 График 1. Фрагмент результатов выполнения п. 3.1 Сравнение результатов, полученных с использованием аналитического и имитационного методов, выводы: Результаты, полученными двумя методами, практически совпадают. Для достижения такой точности, мы рассчитывали производную не на концах отрезков, а на серединах интервалов. Точно так же, как и в имитационном методе. Погрешность вычислений падает с увеличением шагов, так как соотношение шага и величины на начальных значениях влечет за собой большую погрешность в процентном соотношении и создает иллюзию того, что программа не работает. Постановка задачи к п. 2: 3.2. Реализовать имитационное моделирование вычислительной системы на основе принципа δz с целью оценки эффективности ее функционирования. Известно, что вычислительная система состоит из двух компьютеров, интервалы времени между двумя последовательными поступлениями заданий подчиняются равномерному закону распределения с заданными параметрами (см. табл. 1). Перед компьютерами имеется очередь заданий, не превышающая 3 задач. Время выполнения заданий также равномерно распределено (см. табл. 1). 3.2.1. Сымитировать обработку 1000 заданий. 3.2.2. Оценить выходные характеристики изучаемой вычислительной системы: среднее время нахождения задания в очереди; среднее время пребывания задания в системе; вероятности простоя компьютеров. 3.2.3. Повторить имитационный эксперимент 100 раз. Рассчитать характеристики работы системы п. 2.2. по результатам 100 экспериментов. 3.2.4. Сделать выводы. Оценить эффективность работы вычислительной системы. Блок-схема алгоритма имитации работы СМО: 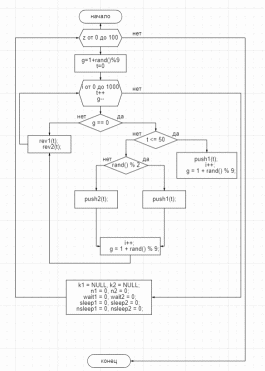 Листинг программы на С++: #include #include #include #include #include #include using namespace std; #define N int(1000) //время ожидания int Twaiting = 0; int Twaiting1 = 0; int Twaiting2 = 0; float Twaitingmiddle; //время ожидания задач int Tprostoy; int Tprostoy1; int Tprostoy2; int t = 0; //время int n1 = 0, n2 = 0;// // число задач в очереди // время окончания выполнения //int Tfinishtobs = 0; int Tfinishtobs1 = 0; int Tfinishtobs2 = 0; int Tarrival1; int Tarrival2; class task { public: int Tintarrival, Tintobs, Tstartobs;//интервал прихода,интервал обслуживания,начало выполнения task(int x, int y) { Tintarrival = x; //время прихода Tintobs = y; //интервал обслуживания } task() { Tintarrival = 0; Tintobs = 0; } void checkt(int num) { Tprostoy = 0; //обнуляем простой Twaiting = 0; if (num == 1) { Tarrival1 = Tintarrival;// приход на первый пк if (Tarrival1 <= Tfinishtobs1) // канал занят { Tstartobs = Tfinishtobs1; Twaiting = Tfinishtobs1 - Tarrival1; Tfinishtobs1 += Tintobs; //Tfinishtobs += Tintobs; Twaiting1 += Twaiting; } else { Tstartobs = Tarrival1; Tprostoy = Tarrival1 - Tfinishtobs1; Tfinishtobs1 = Tstartobs + Tintobs; //Tfinishtobs += Tintobs; Tprostoy1 += Tprostoy; } } else { Tarrival2 = Tintarrival;// приход на второй пк if (Tarrival2 <= Tfinishtobs2) // канал занят { Tstartobs = Tfinishtobs2; Twaiting = Tfinishtobs2 - Tarrival2; Tfinishtobs2 += Tintobs; //Tfinishtobs += Tintobs; Twaiting2 += Twaiting; } else { Tstartobs = Tarrival2; Tprostoy = Tarrival2 - Tfinishtobs2; Tfinishtobs2 = Tstartobs + Tintobs; Tprostoy2 += Tprostoy; //Tfinishtobs += Tintobs; } } } }; class comp { friend class task; public: void checkc(task a, int num) { a.checkt(num); } }; comp PC[2]; task Task[N]; int Getrandomnumber(int min, int max) { int num = 0; num = min + rand() % (max - min + 1); return num; } void setPCFromTask(int i, int t) // задаем комп для выполнения задачи { if (t <= 50) { PC[0].checkc(Task[i], 1); } else { int num; num = Getrandomnumber(1, 2); if (num == 1) { PC[0].checkc(Task[i], 1); } else { PC[1].checkc(Task[i], 2); } } } int main() { setlocale(LC_ALL, "Russian"); SetConsoleCP(1251); SetConsoleOutputCP(1251); srand(time(NULL)); //int g = interval; for (int j = 0; j < 10; j++) { int i = 0; int interval = Getrandomnumber(1, 9); //интервал прихода for (; i < 100; t++, interval--) { if (interval == 0) { Task[i] = task(t, Getrandomnumber(1, 20)); setPCFromTask(i, t); i++; interval = Getrandomnumber(1, 9); //g = interval; } } printf("1 компьютер:\nОжидание: %d\nСон: %d\n\n2 компьютер\nОжидание: %d\nСон: %d\n\nОбщее время выполнения: %d\nВероятность простоя: %f\n__________________________________________\n", Twaiting1, Tprostoy1, Twaiting2, Tprostoy2, t, 1. * (Tprostoy1 + Tprostoy2) / t); Twaiting1 = 0; //Tprostoy1 = 0; Twaiting2 = 0; //Tprostoy2 = 0; t = 0; //Task[N] ; } } Результаты работы программы: 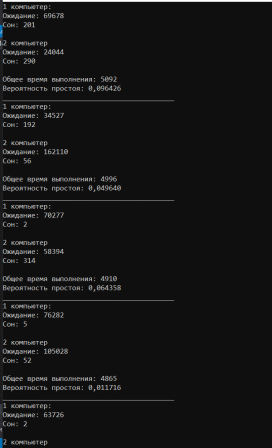 Вывод об эффективности функционирования СМО: Данная СМО имеет очень маленькую вероятность простоя, но время ожидания будет достаточно большим. Это вызвано тем, что компьютеры не успевают обрабатывать поступающие задачи. Возможно, если добавить приоритет по загруженности. Вывод: Мы изучили принципы построения моделирующих алгоритмов: принцип 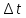 и принцип особых состояний δz. Помимо этого, мы приобрели навыки построения имитационных моделей согласно принципам и принцип особых состояний δz. Помимо этого, мы приобрели навыки построения имитационных моделей согласно принципам 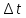 и δz на примере моделирования работы простейших систем. и δz на примере моделирования работы простейших систем. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||