Системы автоматизированного проектирования. Лабораторная № 1. ЛР№1. Отчет по лабораторной работе 1 Прогнозирование объема продаж продукции с помощью моделей и методов регрессионного анализа

• Название: Отчет по лабораторной работе 1 Прогнозирование объема продаж продукции с помощью моделей и методов регрессионного анализа
• Анкор: Системы автоматизированного проектирования. Лабораторная № 1
• Дата: 27.11.2022
• Размер: 3.11 Mb.
• Имя файла: ЛР№1.docx
• Тип: Отчет; #815935

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ,
СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ



ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»

(СПбГУТ)

Факультет Информационных систем и технологий

Кафедра Интеллектуальных систем автоматизации и управления

Системный анализ и принятие решений

Отчет по лабораторной работе №1
«Прогнозирование объема продаж продукции с помощью моделей и
методов регрессионного анализа»

Выполнил:

Студент гр. ИСТ-911

Зотова А.С.
Проверил:

ассистент Шабанов А.П.
Санкт-Петербург

2021
Цель выполнения работы

Цель выполнения лабораторной работы – освоение методологии краткосрочного прогнозирования объема продаж продукции с использованием моделей и методов регрессионного анализа и программы Statistica.

Постановка задачи

Имеется совокупность результатов наблюдений за поведением переменной Y в зависимости от изменения одной или нескольких независимых переменных X (X₁, X₂, …, X_n). Необходимо установить количественную взаимосвязь между показателем Y и факторами X, т.е. определить такую функциональную зависимостьY*=f(X₁,X₂, …, X_n), которая наилучшим образом описывает имеющиеся экспериментальные данные. На основании построенного уравнения регрессии требуется спрогнозировать значение зависимой переменнойYна шаг вперед (момент времени (t+1)) при условии, что значения влияющих факторов на этот период известны.

Описание метода решения задачи

Математическое уравнение, которое описывает линию простой (парной) линейной регрессии с учетом влияния одного фактора, имеет вид:

Y_t+1=b₀+b₁X,

гдеY_t+1 – прогнозное значение зависимой переменной на момент времени (t+1);

b₀,b₁ – параметры, которые оцениваются на основе статистических данных (угловые коэффициенты или коэффициенты регрессии);

X – значение влияющего фактора (независимая переменная).

Однофакторная линейная регрессионная модель может быть расширена путем включения в нее более одной независимой переменной. При совместном влиянии на Y нескольких факторов (X₁, X₂, …, X_n), уравнение множественной регрессии принимает вид:

Y_t+1=b₀+b₁X₁+b₂X₂+…+b_nX_n,

гдеn – число факторов.

Коэффициенты регрессии представляют собой независимые вклады каждой независимой переменной в предсказание зависимой переменной. Если коэффициент b положителен, то связь переменной с зависимой переменной положительна, если коэффициент отрицателен, то и связь носит отрицательный характер (чем меньше значение фактора, тем больше значение переменной Y). Если b=0, то связь между переменными отсутствует. Для проверки гипотезы о нулевых значениях коэффициентов регрессии (т.е. об отсутствии связи между Y и совокупностью факторов) анализируются значения F-статистики Фишера. F-критерий определяется отношением дисперсии оценки модели к дисперсии остатка и равен:

F= ,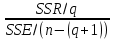

гдеSSR – сумма квадратов, объясненная уравнением регрессии (SumofSquaresaboutRegression);

SSE – сумма квадратов остатков (Sum of Squares Errors);

n – число наблюдений.

q – число коэффициентов регрессии.

Гипотеза об отсутствии линейной зависимости между переменной Y и факторами Xотклоняется при больших значениях F-критерия и значении p-level меньше 0,05 (вероятность ошибочной оценки относительно принятой гипотезы не превышает 5% уровня).

Наиболее простым методом определения коэффициентов регрессии является метод наименьших квадратов (МНК). С помощью этого метода параметры регрессионной модели вычисляются таким образом, чтобы сумма квадратов ошибок (расстояний от линии регрессии до фактических значений данных) была бы минимальной.

Функция ошибки при этом равна:

f = (b₀ + b₁x₁₁ + b₂x₂₁ + … + b_kx_k1 – y₁)² + (b₀ + b₁x₁₂ + b₂x₂₂ + … + b_kx_k2 – y₂)² + …………… + + (b₀ + b₁x_1n + b₂x_2n + … + b_kx_kn – y_n)²

Минимизируя функцию f положим: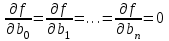

.

Для определения коэффициентов модели множественной линейной регрессии, используя систему уравнений, получим систему нормальных линейных уравнений, которая в векторно–матричной форме имеет вид: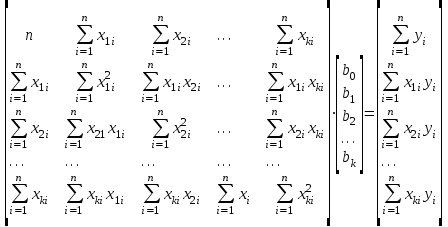

,

где n - число экспериментальных точек;

i - номер точки.

Отклонение отдельной точки от линии регрессии (предсказанного значения) называется остатком. Чем меньше разброс значений остатков около линии регрессии по отношению к общему разбросу значений, тем лучше прогноз. Оценка качества линейной регрессии проводится с помощью коэффициента детерминации R², который показывает какая доля дисперсии отклика объясняется влиянием независимых переменных в построенной модели.

R²=SSR / SST, где

SST – полная сумма квадратов (TotalSumofSquares).

Если связь между переменными X и Y отсутствует, то отношение остаточной изменчивости переменной Y к исходной дисперсии равно 1. Если X и Y коррелируют между собой, то остаточная изменчивость отсутствует и отношение дисперсий будет равно 0. Например, если имеется R²=0,4, то изменчивость значений переменной Y около линии регрессии составляет 1-0,4 от исходной дисперсии, т.е. 40% от исходной изменчивости могут быть объяснены, а 60% остаточной изменчивости остаются необъясненными. Значение R² является индикатором степени подгонки модели к данным (значение R² близкое к 1показывает, что модель объясняет почти всю изменчивость соответствующих переменных). При поиске лучшей регрессионной модели руководствуются требованием R²≥0,8.

Вариант 1

Описание деловой ситуации

Пусть предприятие работает на рынке определенного продукта. При формировании маркетингового решения возникла необходимость в прогнозировании уровня платежеспособного спроса (объема продаж) на выпускаемую продукцию.

Для решения задачи краткосрочного прогнозирования спроса предполагается использовать модели и методы регрессионного анализа.

Маркетологи фирмы располагают статистическими данными за период, равный 30 месяцам, о фактических значениях объемов продаж продукции по месяцам, расходах на рекламу по месяцам, ценах на продукцию фирмы и на продукцию конкурирующей фирмы (см. табл. 1). Такие факторы, как расходы на рекламу, цена на продукцию фирмы и ее основного конкурента были выбраны как наиболее значимые по степени влияния на выходной показатель – объем продаж продукции.

Требуется: 1. Рассчитать ожидаемый предприятием объем продаж продукции на 31-й месяц работы при условии, что предполагаемые на этот месяц значения факторов, влияющих на объем продаж, составят: расходы на рекламу – 93 тыс. руб., цена единицы продукции – 340 руб., цена единицы продукции конкурирующей фирмы – 343 руб.

2. Построить последовательно однофакторную линейную регрессионную модель (с учетом только одного фактора – расходов на рекламу), двухфакторную линейную регрессионную модель (с учетом таких факторов, как расходы на рекламу и цена единицы продукции предприятия) и трехфакторную линейную регрессионную модель (с учетом трех факторов - расходы на рекламу, цена единицы продукции предприятия и цена на единицу продукции фирмы-конкурента).

3. Рассчитать оценки прогнозов объема продаж в 31 месяце, используя построенные регрессионные модели.

4. Провести сравнительный анализ прогнозных оценок объемов продаж продукции, полученных с помощью однофакторной, двухфакторной и трехфакторной регрессионных моделей.

При поиске лучшей регрессионной модели следует руководствоваться следующими наиболее общими требованиями:

1. 
   Регрессионная модель должна объяснять не менее 80% вариации зависимой переменной, т.е. R² 0.8.
   
2. 
   Стандартная ошибка оценки зависимой переменной по уравнению должна составлять не более 5% среднего значения зависимой переменной;
   
3. 
   Коэффициенты уравнения регрессии и его свободный член должны быть значимы на 5%-ом уровне.
   
4. 
   Остатки от регрессии должны быть нормально распределены и без систематической составляющей.
   

Таблица 1. Исходные данные для прогнозирования спроса

Номер месяца (t)	Фактический объем продаж за месяц (тыс.руб.) (Y)	Расходы на рекламу за месяц (тыс. руб.) (X1)	Цена продукта (руб./ед. продукта) (X2)	Цена продукта фирмы-конкурента (руб./ед. продукта) (X3)
1	268	58	287	290
2	300	52	289	291
3	297	50	290	292
4	290	51	279	295
5	274	53	278	293
6	263	49	283	296
7	285	53	291	295
8	282	59	293	295
9	254	60	293	297
10	297	57	289	292
11	257	57	289	292
12	289	55	294	295
13	291	62	299	302
14	290	68	301	304
15	290	67	301	304
16	249	75	299	305
17	282	63	315	318
18	285	64	318	322
19	254	69	313	320
20	299	70	302	308
21	296	75	321	327
22	276	74	334	339
23	246	74	334	339
24	246	79	328	330
25	246	79	328	330
26		87	331	336

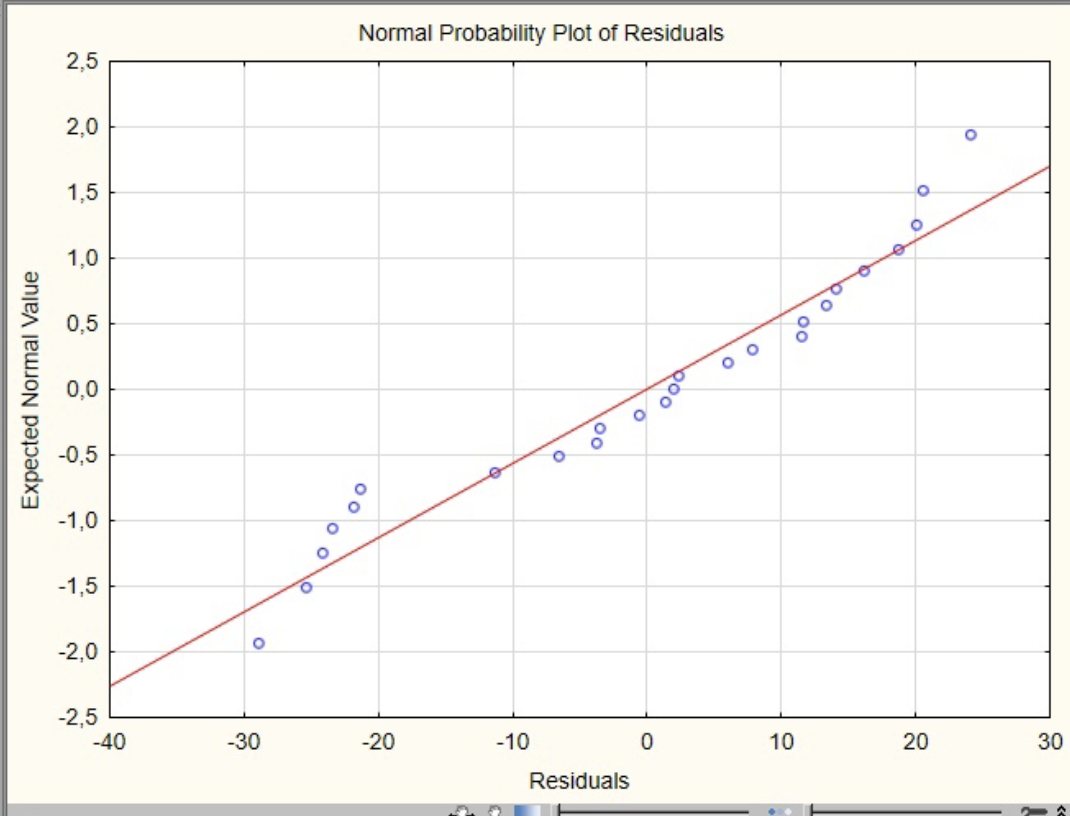
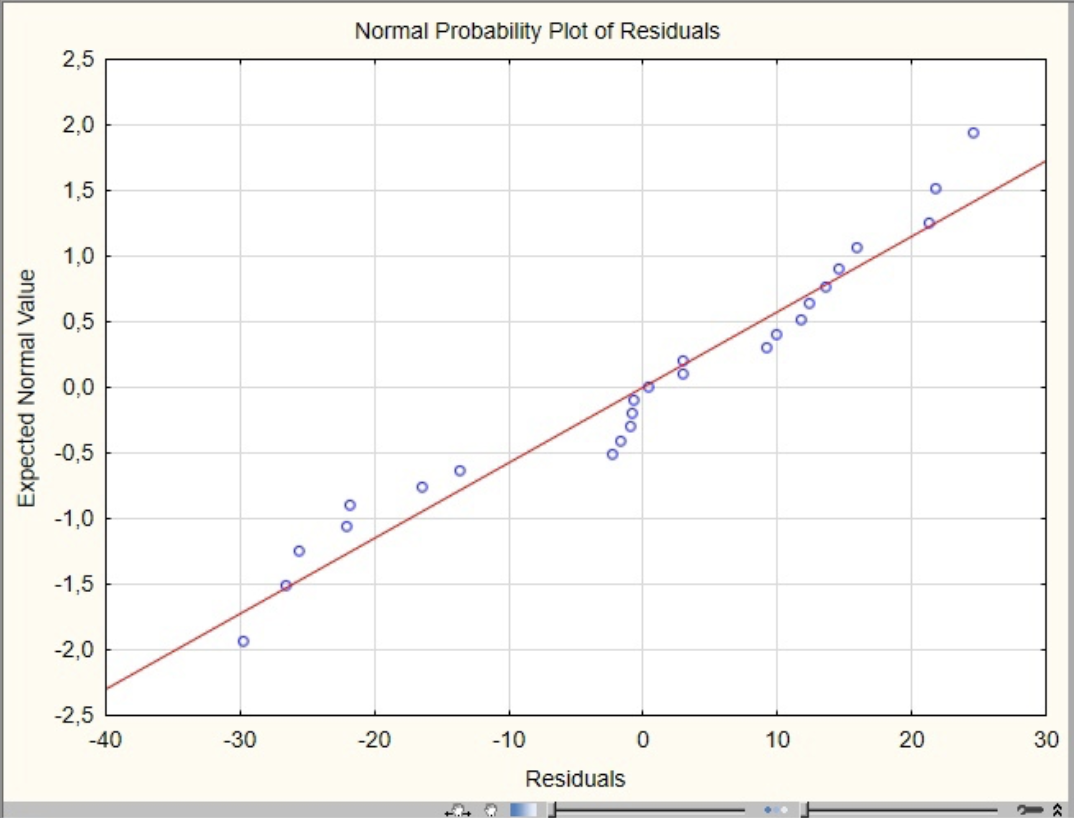
Анализ результатов решения задачи

В программе Statistica задаются исходные данные по 26 месяцам из таблицы 1.

1. 
   Проводится построение однофакторной линейной регрессионной модели (с учетом одного фактора – расходов на рекламу) вида Y=b₀+b₁X₁. Коэффициенты регрессии b₀, b₁, рассчитанные для однофакторной модели представлены на рисунке 1.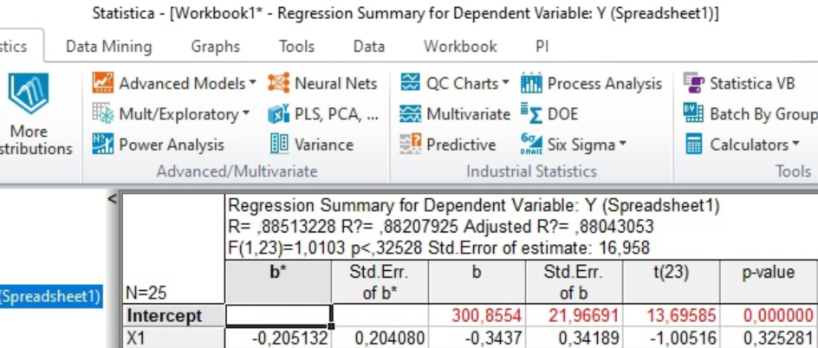
   

Рисунок 1. Итоги регрессионного анализа однофакторной модели
Проведен расчет значений коэффициентов регрессии для модели с учетом влияния фактора «Расходы на рекламу». Выражение однофакторной линейной регрессии можно представить в виде: Y₃₁=300,9-0,34*X₁.

Расчет прогнозного значения объема продаж на 31-й месяц в ручном режиме:

Y₃₁= 300,9-0,34*87=271,32

Прогнозное значение объема продаж на 26-й месяц с учетом влияния расходов на рекламу, полученное в автоматическом режиме Y₃₁=271,32тыс.руб. (рис. 2).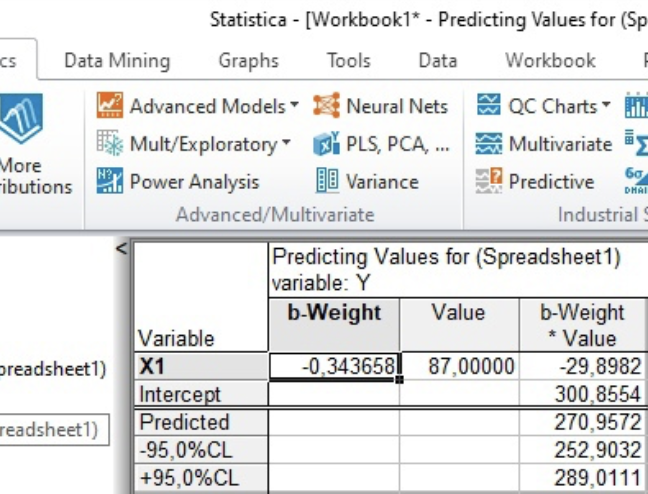



Рисунок 2. Расчет прогнозного значения объема продаж с использованием однофакторной линейной регрессионной модели

2. 
   Строится двухфакторная линейная регрессионная модель (с учетом двух факторов – расходов на рекламу и цены единицы продукции) вида Y=b₀+b₁X₁+b₂X₂. Значения коэффициентов регрессии b₀, b₁, b₂ представлены на рисунке 3.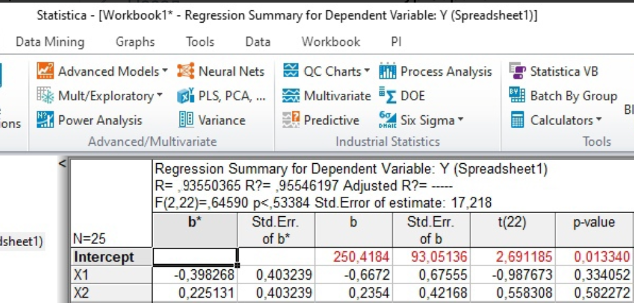
   

Рисунок 3. Итоги регрессионного анализа двухфакторной модели
Проведен расчет значений коэффициентов регрессии для модели с учетом влияния факторов «Расходы на рекламу» и «Цена единицы продукции». Выражение двухфакторной линейной регрессии можно представить в виде: Y₃₁=250,4-0,7*X₁+0,2*X_2.

Расчет прогнозного значения объема продаж на 31-й месяц в ручном режиме:

Y₃₁=250,4-0,7*87+0,2*331 = 255,7

Прогнозное значение объема продаж на 31-й месяц с учетом влияния расходов на рекламу и цены единицы продукции предприятия, полученное в автоматическом режиме составляет Y₃₁=255,7 тыс.руб.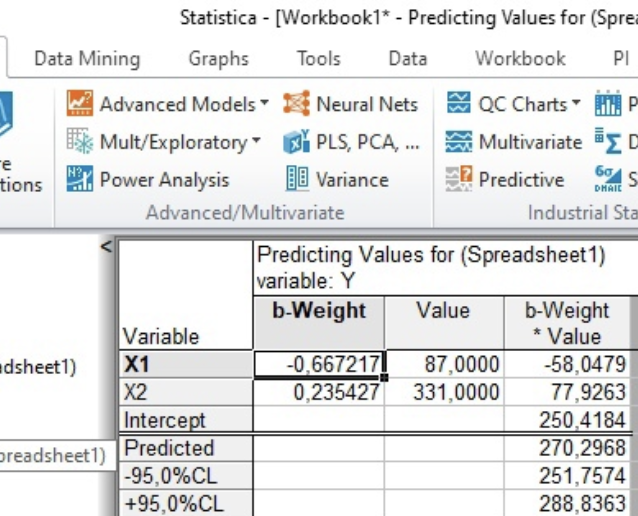



Рисунок 4. Расчет прогнозного значения объема продаж при использовании двухфакторной регрессионной модели

3. 
   Значения коэффициентов регрессии b₀, b₁, b₂, b₃, рассчитанные для трехфакторной линейной регрессионной модели (с учетом трех факторов – расходов на рекламу, цены единицы продукции предприятия и цены единицы продукции фирмы-конкурента) вида Y=b₀+b₁X₁+b₂X₂+b₃X₃, представлены на рисунке 5.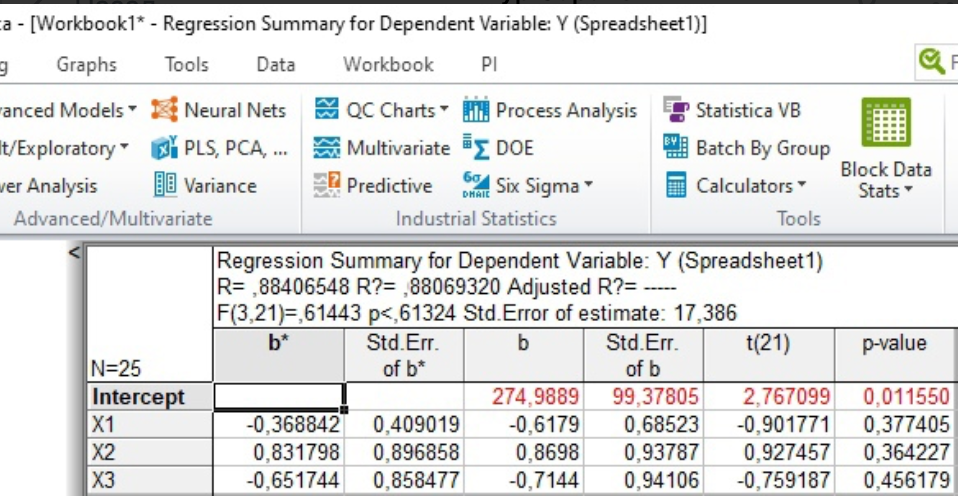
   

Рисунок 5. Итоги регрессионного анализа трехфакторной модели
Проведен расчет значений коэффициентов регрессии для модели с учетом влияния факторов «Расходы на рекламу», «Цена единицы продукции предприятия» и «Цена единицы продукции фирмы-конкурента». Выражение трехфакторной линейной регрессии можно представить в виде: Y₃₁=274,99-0,62*X₁-0,87*X₂-0,71*Х₃

Расчет прогнозного значения объема продаж на 31-й месяц в ручном режиме:

Y₃₁=274,99-0,62*87+0,87*331-0,71*336=269,88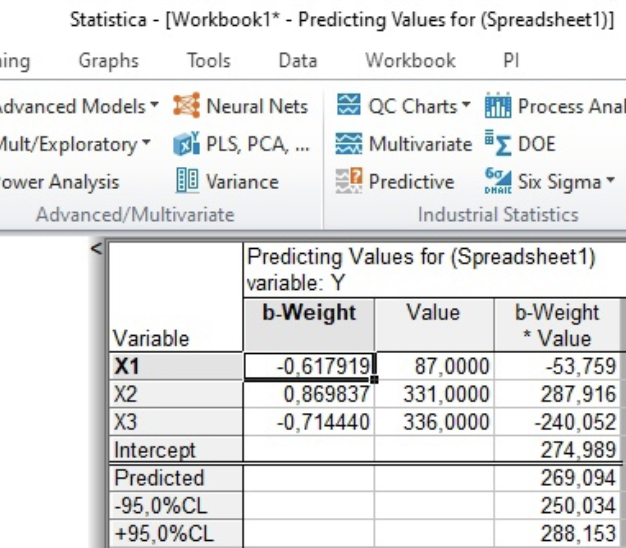



Рисунок 6. Расчет прогнозного значения объема продаж с использованием трехфакторной регрессионной модели
Прогнозное значение объема продаж на 31-й месяц с учетом влияния расходов на рекламу, цены единицы продукции предприятия и цены единицы продукции фирмы-конкурента, полученное в автоматическом режиме Y₃₁=269,88тыс.руб.

Заключение

В ходе лабораторной работы была решена задача прогнозирования объема продаж с применением метода регрессионного анализа. Осуществлено последовательное построение моделей регрессионного анализа с учетом влияния одного, двух и трех рассматриваемых факторов на значение объема продаж для 31 месяца работы предприятия. Анализ построенных моделей показал, что все три модели корректны, имеют значения R²>0,85, т.е. объясняют больше 85% разброса значений переменной Y относительно среднего:

- для однофакторной модели R²=0,885;

- для двухфакторной модели R²=0,955;

- для трехфакторной моделиR²=0,88.

Во всех построенных регрессионных моделях стандартная ошибка оценки зависимой переменной составляет порядка 2,5%, что является допустимой нормой. Построенные регрессии значимы, а гипотеза об отсутствии связи между переменными может быть отклонена, т.к. большим значениям F-критериев соответствуют уровни значимости (p-level) меньше 5%. Результаты получены на последнем шаге регрессии и проведен анализ остатков для каждой регрессионной модели (табл. 2). По графикам можно сделать вывод, что остатки нормально распределены (в пределах ±18 ед.), заметных выбросов нет.

Фактор X₂ (цена единицы продукции предприятия) в двухфакторной и трехфакторной моделях имеет низкий уровень значимости (p-level больше 0,05), т.е. этот фактор в меньшей степени влияет на изменение уровня объема продаж, чем остальные факторы.


Таблица 2. Распределение остатков, полученных по результатам

построенных регрессионных моделей

Распределение остатков однофакторной регрессионной модели	Распределение остатков двухфакторной регрессионной модели	Распределение остатков трехфакторной регрессионной модели

Таким образом, каждая из построенных регрессионных моделей может быть использована для решения задачи прогнозирования объема продаж продукции предприятия. Окончательным решением задачи прогнозирования будем считать прогнозное значение Y₃₁=269,88 тыс.руб., полученное при использовании трехфакторной регрессионной модели, т.к. этой модели соответствует наиболее высокий уровень коэффициента детерминации R² и наименьший разброс остатков (в пределах ±15 ед.).