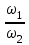Лабораторная работа по химии 12. Лабораторная №12 Толбатов ПГСз-01. Отчет по лабораторной работе 12 Градуировка звукового генератора Выполнил студент группы пгсз01
 Скачать 3.48 Mb. Скачать 3.48 Mb.
|
|
Министерство науки и высшего образования Российской Федерации ФГБОУ ВО «Северо – Восточный Государственный Университет» Политехнический институт Отчет по лабораторной работе №12 Градуировка звукового генератора Выполнил студент группы ПГСз-01 Толбатов Александр Александрович Проверила: преподаватель Гайдай Наталия Константиновна Магадан 2022 год. Цель работы: изучить устройство электронного осциллографа, условия появления фигур Лиссажу. Освоить метод определения неизвестной частоты генератора с помощью фигур Лиссажу и строить градуировочный график. Приборы и материалы: генераторы ГЗ-118, ГЗ-34, осциллограф, соединительные провода. ХОД РАБОТЫ Общий вид установки для проведения работы приведен на фото 1 . Градуировка звукового генератора ГЗ-34 производится с помощью фигур Лиссажу. Для этого:  1. На эталонном генераторе Г3-118 установить опорную частоту 50 Гц (если преподавателем не указана другая опорная частота 1. На эталонном генераторе Г3-118 установить опорную частоту 50 Гц (если преподавателем не указана другая опорная частота 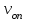 ) (фото 2 ). ) (фото 2 ). 2. На обоих генераторах установить множитель 1 (ручки осциллографа не трогать). 2. На обоих генераторах установить множитель 1 (ручки осциллографа не трогать).3. Вращая рукоятку регулировки частоты градуируемого генератора Г3-34 добиться на экране появления устойчивой фигуры Лиссажу. 4. Используя таблицу фигур Лиссажу и значение известной частоты эталонного генератора определить значение частоты для генератора Г3-34 (таблица фигур Лиссажу и соотношения частот расположена в лаборатории, примеры фигур Лиссажу, появляющихся на экране осциллографа, приведены фото 4). Например: На экране осциллографа «картинка» выглядит в виде эллипса Если на экране осциллографа появилась фигура 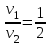 , где , где 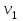 - опорная частота. Например, если - опорная частота. Например, если 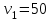 Гц, то Гц, то 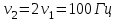 . . Отношение частот изменится, если фигура повернется на 900: 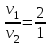 и и 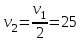 Гц (при опорной частоте 50 Гц). Гц (при опорной частоте 50 Гц). Подобным образом определяем частоты, соответствующие всем числам Подобным образом определяем частоты, соответствующие всем числам на лимбе ГЗ-34 (фото 5). 5. Записать в таблицу 1 значение деления лимба N генератора ГЗ-34 и соответствующую ему частоту.  Построить график зависимости частоты от значений делений на лимбе Построить график зависимости частоты от значений делений на лимбе 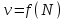 . .Примечание. С целью увеличения количества точек для построения градуировочного графика, измерения можно провести еще для одной-двух различных опорных частот. Таблица 1. Определение частоты генератора Г3-34 при частоте 62 Гц.
Таблица 2. Определение частоты генератора Г3-34 при частоте 46 Гц.
График 1 График зависимости частоты от значений делений на лимбе 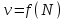 при частоте 46 Гц. при частоте 46 Гц.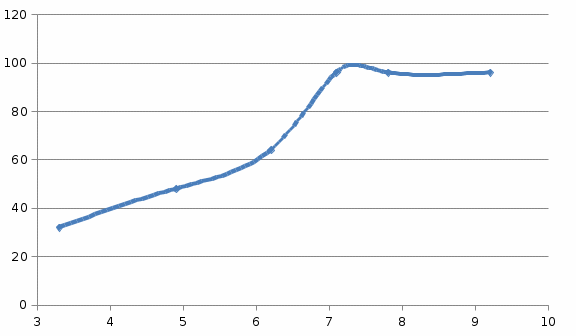 График 2 График зависимости частоты от значений делений на лимбе 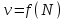 при частоте 62 Гц. при частоте 62 Гц.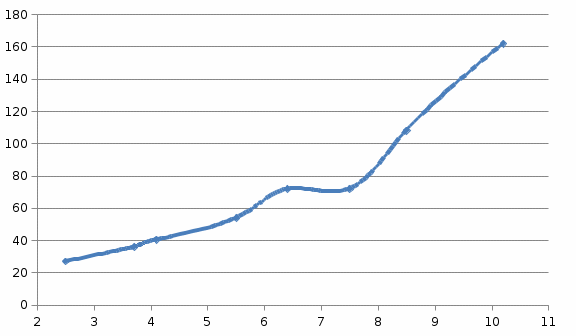 Ответ на теоретический вопрос. Колебания — повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия. Гармоническое колебание — колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону. Кинематическое уравнение гармонических колебаний имеет вид или где х — смещение (отклонение) колеблющейся точки от положения равновесия в момент времени t; А — амплитуда колебаний, это величина, определяющая максимальное отклонение колеблющейся точки от положения равновесия; ω — циклическая частота, величина, показывающая число полных колебаний происходящих в течение 2π секунд Амплитуда — максимальное значение смещения или изменения переменной величины от среднего значения при колебательном или волновом движении. Амплитуда и начальная фаза колебаний определяется начальными условиями движения, т.е. положением и скоростью материальной точки в момент t=0. Обобщенное гармоническое колебание в дифференциальном виде амплитуда звуковых волн и аудиосигналов обычно относится к амплитуде давления воздуха в волне, но иногда описывается как амплитуда смещения относительно равновесия (воздуха или диафрагмы говорящего) Чaстота — физическая величина, характеристика периодического процесса, равная числу полных циклов процесса, совершённых за единицу времени. Частота колебаний в звуковых волнах определяется частотой колебаний источника. Колебания высокой частоты затухают быстрее низкочастотных. Величина, обратная частоте колебаний Период колебаний- длительность одного полного цикла колебаний. Т=1/ |